我们知道,布丁在外力的作用下,很容易发生形变。并且,由于布丁具有弹性,在形变之后会来回晃动。今天我们用 Shader 来模拟布丁晃动的效果。
老规矩,先来看一下最终效果:
一、位置和形状
1、控制层
一开始,我们拿到的只是一张静态的图片。所以第一步要做的,是确定布丁在图片的哪个区域。
先来明确下思路:布丁的位置和形状由用户来确定,需要在 UIKit 层完成这个交互。在确定之后,需要把对应的位置和形状信息传递给 Shader,为后面的动画模拟做准备。
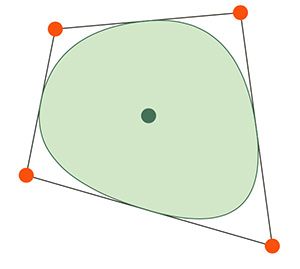
由于布丁可能是椭圆形或者类圆形,所以不能简单只用一个圆心和半径来确定。我们需要一种更灵活的控制方式。
最终采取的方案如下:用 4 个顶点来控制 4 条贝塞尔曲线。以每条边的中点作为起始点和终止点,顶点作为控制点来绘制贝塞尔曲线,4 条贝塞尔曲线形成一个封闭的类圆形。如下图所示:
尽管这样的控制方式仍然不足以囊括所有的形状,但是相比圆形,灵活度已经有了很大的提高。
另外,可以看到中心还有一个绿色的圆点,这个也是允许用户控制的一个维度,用来表示布丁的中心位置。主要与模拟晃动效果相关,具体有什么用后面会说到。
于是,在控制层,用户可以通过控制 5 个点的坐标,用来确定布丁的形状和中心。
2、数据传递
通过上个步骤,我们拿到了位置和形状信息。接下来则是把这些信息告诉 Shader,然后在动画执行的时候,Shader 可以通过计算,对目标区域内的点进行偏移处理。
先来看一下塞尔曲线的方程:P = (1 - t)^2 * P0 + 2 * t * (1 - t) * P1 + t^2 * P2
注:
P0是起始点、P1是控制点、P2是终止点,这三点都是已知点,唯一的变量是t,t的取值范围是 0 ~ 1 。
因为贝塞尔曲线有具体的方程式,所以我们只需要传递关键点(起始点、终止点、控制点)的坐标,然后在 Shader 里去计算位置关系。
因为 UIKit 的坐标和纹理坐标存在差异,所以在传递之前有一个转换过程,转换代码如下:
MFWobbleModel *wobbleModel = [[MFWobbleModel alloc] init];
wobbleModel.pointLT = CGPointMake(model.pointLT.x / width, 1 - (model.pointLT.y / height));
wobbleModel.pointRT = CGPointMake(model.pointRT.x / width, 1 - (model.pointRT.y / height));
wobbleModel.pointRB = CGPointMake(model.pointRB.x / width, 1 - (model.pointRB.y / height));
wobbleModel.pointLB = CGPointMake(model.pointLB.x / width, 1 - (model.pointLB.y / height));
wobbleModel.center = CGPointMake(model.center.x / width, 1 - (model.center.y / height));
注:
wobbleModel保存的是纹理坐标,model保存的是 UIKit 坐标。
而传递仍然是用 uniform 变量的方式,我们在之前的文章已经讲过,这里不再赘述。
现在我们在 Shader 中,已经可以拿到贝塞尔曲线方程了,那么要如何判断点与 4 条曲线的位置关系呢?
这是本文的第一个重点。
我们知道,在片段着色器中,每一个片段都会执行一遍片段着色器的代码。所以,我们面临的问题是:已知一个点的纹理坐标,如何判断这个点是否在目标区域内?
先看图,我们根据 4 条贝塞尔曲线和中点,将目标区域划分成了 4 个区域。所以上面的问题可以简化为:已知一个点的纹理坐标,如何判断这个点是否在单条贝塞尔曲线与中点构成的区域内?
具体的步骤如下:
1、将当前点与中点进行连接得到一条直线,求出直线方程。
2、求直线和贝塞尔曲线的交点。
3、如果有交点,判读当前点是否位于交点和中心点之间,在就说明点在区域内,否则就在区域外。
通过上面的步骤,可以判断一个点是否在某条贝塞尔曲线的范围内。如果不在,我们就换另一条曲线继续计算。这样,就能判断点是否落在目标区域里了。
现在思路已经有了,接下来就是具体的求解步骤。
我们知道,直线方程的一般式是:Ax + By + C = 0
已知直线上的两个点 P1(x1, y1)、 P2(x2, y2) ,可以求出对应的参数值:
A = y2 - y1
B = x1 - x2
C = x2 * y1 - x1 * y2
写成代码是:
float getA(vec2 point1, vec2 point2) {
return point2.y - point1.y;
}
float getB(vec2 point1, vec2 point2) {
return point1.x - point2.x;
}
float getC(vec2 point1, vec2 point2) {
return point2.x * point1.y - point1.x * point2.y;
}
此时 A 、B 、C 可以被当成已知数。
上面我们已经提到过贝塞尔曲线的方程,现在将它分别拆成 x 、y 的方程。
x = (1 - t)^2 * x0 + 2 * t * (1 - t) * x1 + t^2 * x2
y = (1 - t)^2 * y0 + 2 * t * (1 - t) * y1 + t^2 * y2
将上面两个方程代入直线方程的一般式 Ax + By + C = 0,可以消去 x 、y,只剩下 t 一个未知数。
然后我们对这个方程进行求解,得出两个解。如下:
写成代码是很长的一串,这里细节就不贴出来了,把它们封装成两个函数:
float getT1(vec2 point1, vec2 point2, vec2 point3, float a, float b, float c) {
float t; // t = ...
return t;
}
float getT2(vec2 point1, vec2 point2, vec2 point3, float a, float b, float c) {
float t; // t = ...
return t;
}
当然,上面的解不是我自己算出来的。这里推荐一个 工具网站 ,它可以很快地帮我们的方程求解。如下图,我们输入消去了 x 、y 后的方程,它就帮我们算出了两个解:
注: 如果你去仔细阅读源码,会发现
getT1、getT2的实现与上图的结果不是完全一致,但其实他们在变形之后还是等价的。这里不用过分关注细节,只需要知道它是我们求交点的一个中间步骤,以及它是怎么来的就可以。
于是,我们可以通过上面的函数求出两个 t 的值,只要 t 满足 0~1 的范围,就说明直线和贝塞尔曲线存在交点。然后把满足条件的 t 代入贝塞尔曲线方程,就可以算出对应的交点坐标。代码如下:
vec2 getPoint(vec2 point1, vec2 point2, vec2 point3, float t) {
vec2 point = pow(1.0 - t, 2.0) * point1 + 2.0 * t * (1.0 - t) * point2 + pow(t, 2.0) * point3;
return point;
}
求出交点之后,判断当前点是否位于交点和中点之间,代码如下:
bool isPointInside(vec2 point, vec2 point1, vec2 point2) {
vec2 tmp1 = point - point1;
vec2 tmp2 = point - point2;
return tmp1.x * tmp2.x <= 0.0 && tmp1.y * tmp2.y <= 0.0;
}
这里返回 true 表示点在区域内,false 则表示点在区域外。
二、物理效果模拟
1、位置偏移
晃动效果的实现,本质上是对目标区域内的点进行不同程度的位置偏移。而每个点的位移规则,决定了最终效果的真实程度。
这是本文的第二个重点。
原本以为,这种物理学相关的现象,应该有现成研究好的公式,我只要套下公式就好了。奈何找了一圈,啥也找不到,也可能是我搜索的姿势不对,那就只好自己瞎编了。
注: 位移的规则直接决定了最终的呈现效果,我这里只说明一下我的规则和实现方式。如果你的数学足够好,可以尝试建立三维坐标系,并将目标区域内的点都映射到空间中的坐标,这样能更加精确地计算出中心点位移对每个点造成的不同位移影响。而我这里只求「差强人意」即可。
我的位移规则如下:
1、位移只跟当前点与中心点的距离有关。距离越大,位移越小,区域边缘的位移为 0。
2、随着与中心点距离的增加,位移呈非线形递减。
第一点应该很好理解,这里主要对第二点的「非线性」做一下解释。
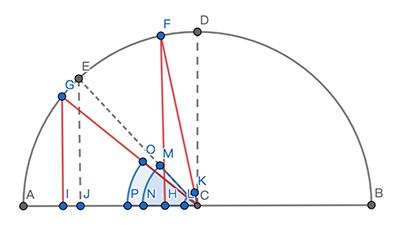
为了实现我们想要的效果,需要将目标区域近似地当成一个半球面来处理。而我们的静态图片是一个俯视图,下面用一个半圆来近似地充当一个正视图。
这里的 D 表示目标区域的中点,E 表示任意一个在目标区域内的点,A 表示上面提到的用 t 算出来的交点。半圆的半径 AC 表示交点到中点的距离。
当 D 点移动到 F 点的时候,E 点会移动到 G 点,并且此时 A 点的位置不变。从俯视图来看,D 点的移动距离是 HC ,E 点的移动距离是 IJ 。我们的最终目的就是通过 HC 来求 IJ 。
我们假定: AD 上所有的点,到 A 的弧长,在 D 点移动前后,所占的弧长比例不变。即 AG / AE = AF / AD 。
所以 IJ 的求解步骤是:
AF = acos(HC / AC) * AC
AE = acos(JC / AC) * AC
AD = (PI / 2) * AC
AG = AE * AF / AD
IJ = AC * (cos(AG / AC) - cos(AE / AC))
对应到代码里是这样:
float centerOffsetAngle = acos(maxCenterDistance / maxDistance);
float currentAngle = acos(distanceToCenter / maxDistance);
float currentOffsetAngle = currentAngle * centerOffsetAngle / (PI / 2.0);
float currentOffset = maxDistance * (cos(currentOffsetAngle) - cos(currentAngle));
简单来说,就是根据点到中心的距离 distanceToCenter ,来求出点的位移 currentOffset 。
2、阻力模拟
由于布丁具有弹性,在形变之后,会累积弹性势能。所以越靠近边缘,阻力越大。因此在中间的时候,移动速度比较快,在边缘的时候,移动速度比较慢。
这里用 Easeout 缓动函数来模拟这种先快后慢的效果。但遗憾的是 GLSL 中没有提供现成的函数。
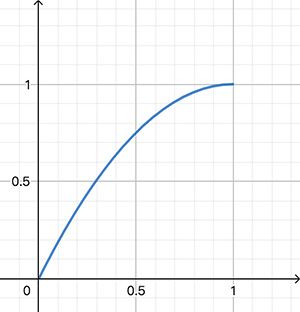
我们来看下方程 y = 2 * x - x ^ 2,它的图像如下:
可以看到,当 x 从 0 到 1 变化的时候,y 的变化速度是先快后慢。我们正好可以拿它来当 Easeout 缓动函数。
3、振幅衰减
根据能量守恒定律,布丁在每次晃动的时候,由于能量损耗,其具有的动能和弹性势能会逐步衰减。换句话说,布丁每次晃动的幅度都会比上一次小。
这里在每次晃动周期结束后,通过对振幅乘以一个缩小倍数来实现。并且,当振幅小于某个阈值的时候,直接设置为 0 ,表示回到了静止状态。
实际代码如下:
model.amplitude *= 0.7;
model.amplitude = model.amplitude < 0.1 ? 0 : model.amplitude;
三、输入事件处理
通过上面的步骤,我们已经可以拥有一个完整的晃动动画了。最后一步是让动画响应用户的输入事件。
在这一步,我们要做的是把输入事件转化为一个单位方向向量,然后把这个向量传递给 Shader,表示晃动方向。
这里对两种输入事件进行处理:屏幕触摸,加速计。
1、触摸事件
当手指触摸屏幕的时候,判断触摸点是否在目标区域的范围内。如果在,则在手指移动的时候,根据手指的移动方向,去决定单位向量的方向。
关键代码如下:
- (void)touchesBegan:(NSSet *)touches withEvent:(UIEvent *)event {
[super touchesBegan:touches withEvent:event];
CGPoint currentPoint = [[touches anyObject] locationInView:self];
currentPoint = CGPointMake(currentPoint.x / self.bounds.size.width, 1 - (currentPoint.y / self.bounds.size.height)); // 归一化
for (MFWobbleModel *model in self.wobbleModels) {
if ([model containsPoint:currentPoint]) {
self.currentTouchModel = model;
self.startPoint = currentPoint;
break;
}
}
}
- (void)touchesMoved:(NSSet *)touches withEvent:(UIEvent *)event {
[super touchesMoved:touches withEvent:event];
if (self.currentTouchModel) {
CGPoint currentPoint = [[touches anyObject] locationInView:self];
currentPoint = CGPointMake(currentPoint.x / self.bounds.size.width, 1 - (currentPoint.y / self.bounds.size.height)); // 归一化
CGFloat distance = sqrt(pow(self.startPoint.x - currentPoint.x, 2.0) + pow(self.startPoint.y - currentPoint.y, 2.0));
CGPoint direction = CGPointMake((currentPoint.x - self.startPoint.x) / distance, ((currentPoint.y - self.startPoint.y) / distance));
[self startAnimationWithModel:self.currentTouchModel direction:direction amplitude:1.0];
self.currentTouchModel = nil;
}
}
2、加速计
这里对加速计的详细使用方式并不展开。我们只需要添加一个监听,则在手机晃动的时候,可以在回调里拿到加速度值的变化,从而确定方向。
关键代码如下:
self.motionManager.accelerometerUpdateInterval = 0.1; // 0.1 秒检测一次
__weak typeof(self) weakSelf = self;
[self.motionManager startAccelerometerUpdatesToQueue:[[NSOperationQueue alloc] init] withHandler:^(CMAccelerometerData *accelerometerData, NSError *error) {
CMAcceleration acceleration = accelerometerData.acceleration;
CGFloat sensitivity = sqrt(pow(acceleration.x, 2.0) + pow(acceleration.y, 2.0));
if (sensitivity > 1.0) {
CGPoint direction = CGPointMake(acceleration.x / sensitivity, acceleration.y / sensitivity);
for (MFWobbleModel *model in weakSelf.wobbleModels) {
// 当前的振幅小于某个阈值才会受影响
if (model.amplitude < 0.3) {
[weakSelf startAnimationWithModel:model direction:direction amplitude:1.0];
}
}
}
}];
至此,我们就得到一个完美的布丁了。
最后,完整流程走一遍:
源码
请到 GitHub 上查看完整代码。
参考
- 贝塞尔曲线_百度百科
- 推荐一个数学工具网站
- 缓动公式小析
获取更佳的阅读体验,请访问原文地址【Lyman's Blog】GLSL 与布丁晃动艺术