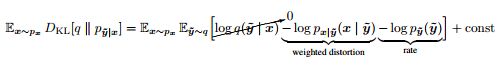c语言图像压缩算法实现_Image Compression 图像压缩
随着互联网技术的飞速发展,对于图像/视频数据的存储、传输等实际应用的需求也不断扩增。今天来简单介绍一下近期调研学习的,基于深度学习的图像压缩算法。
End-to-End Optimized Image Compression
文章来自ICLR2017,算法由analysis transform、uniform quantizer 和 synthesis transform组成。analysis transform过程包含三个重复阶段,每个阶段包括卷积线性滤波器+非线性激活函数,联合非线性的目的在于实现局部增益控制。由于uniform quantizer带来了梯度不可导,故引入proxy function代理函数实现网络端到端训练。松弛的损失函数可以看做通过VAE生成模型的对数似然,算法在PSNR、MS-SSIM测量指标下均优于JPEG及JPEG-2000方法。
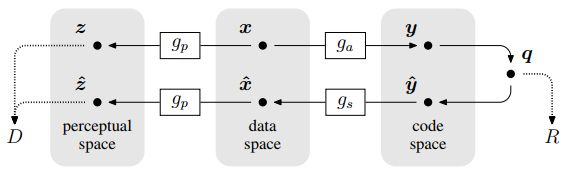
如上图所示,算法在编码空间将图像进行编码压缩得到R;转换至感知空间,计算图像的失真率D。
下图为算法的分析(编码)和合成(解码)模块。分别使用了升降采样,GDN、IGDN结构。
GDN和IGDN
在Autoencoder模块中,使用了GDN[1](generalized divisive normalization)进行归一化处理。其类似一般CNN网络中的Batch Normalization作用,可以很好的捕捉图像的统计特性,并将其转换为高斯分布。GDN/IGDN公式如下,对应的在decoder阶段,使用GDN的逆IGND参与网络学习。下式中,k代表stage阶段序号,i,j代表像素位置。
针对本文的更多细节这里不再展开,继续看下一篇~
Variational image compression with a scale Hyper-prior[2]
文章来自ICLR2018谷歌团队。这篇论文可谓答疑解惑之良药,之前阅读《Joint Autoregressive and Hierarchical Priors for Learned Image Compression》完全云里雾里的,原来是打开方式不对,应该先读读这篇“绪论”。
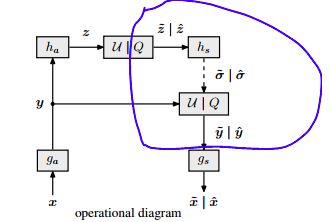
算法提出complex prior,也就是hierarchical模块(下图右),和autoencoder 模块(下图左):
可以看到右下角hs模块产出的信号
hierarchical priors
为什么要引入这个hierarchical priors模块?原因在于,图像压缩其实是学习图像的信号分布过程。对于待压缩图像x,我们不知道它的实际分布,且它的分布是存在统计依赖(概率耦合)的,因此需要剔除这部分冗余,实现最优压缩。
上图中,2、3子图均可隐约看出图像的大致轮廓,即一些高对比度,边缘纹理等特征(
论文中提到的,模拟一组目标变量之间依赖关系的标准方法是引入潜在变量,条件是假定目标变量是独立的。我们引入了额外的
上图蓝色部分学习得到的,即为原图像的标准差的空间分部信息,也是hierarchical priors模块的主要目的产物。
整体算法的损失函数由KL散度推导而来,即图像压缩比及失真率的trade-off,这一设计也被后续的压缩算法传承运用。
uniform noise
另外再补充一点,由于算法引入了量化模块Q,为了实现随机梯度优化,在网络训练时需要添加均匀噪声uniform noise “放松模型”,完成参数优化。
Results
算法在Kodak数据集上检测性能,MS-SSIM指标达到最优,PSNR略次于BPG方法。
Joint Auto-regressive and Hierarchical Priors for Learned Image Compression
有了论文[2]的阅读基础,理解这篇同样来自谷歌团队的nips2018文章就会轻松一些。文章提出一种结合层级先验 hierarchical priors、自回归Auto-regressive、上下文信息 context of image 等策略的图像压缩算法。算法在PSNR、MS-SSIM等图像指标上均超过BPG方法。可以发现,本篇文章的改进点在于自回归思想及上下文信息的使用。算法框架如下:
上图蓝色框内,算法增加了图像上下文信息模块,及学习熵编码模块中的均值和标准差模块。对比[2]中多学习均值统计量。另外在上图虚线框模块中,结合边信息(Hyper Decoder)和上下文信息(context info)预测熵编码中的概率值。换个角度看,算法基于[3]中的 Gaussian scale mixture (GSM)模型提出的Gaussian mixture model(GMM)高斯混合模型。通过学习两个高斯分布,或者说基于某一已知分布,推算另一数据分布的条件概率值。(个人理解观点,如有错误还请指正) 这就涉及到了我们想要的
再来看看算法各个模块中的网络层设计:
稍微注意一下,最后的entropy parameters模块中的channel通道数是auto-coder中的2倍。这也很好理解,因为这个模块需要学习均值和方差两个参数。
依次看一下论文的两个公式:
类似[2]中的,损失函数采用压缩比与失真率两个指标的trade-off。由于本文涉及多一层的Hyper encoder,故上式中添加了此部分loss计算。
Deep Image Compression using Decoder Side Information
最后介绍一篇arxiv2020的工作《Deep Image Compression using Decoder Side Information》 论文引入side information辅助decoder端进行快速图像解码。注意这个side information和以上几篇论文中的边信息不是同一概念啊,别混淆了。且side information 仅作用在decoder端。
先看算法框架:
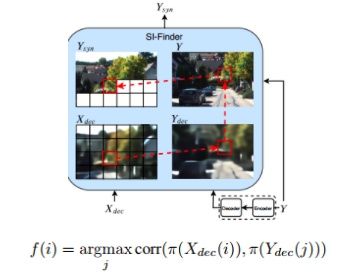
同样是auto-encoder模块进行图像编码和解码,初步获得Xdec信号。紧接着,信号流接入SI-Finder模块,实现图像“边”信息提取。在这个模块中生成Ysyn信号,Ysyn信号辅助Xdec信号一起完成图像重建(SI-Net)。
思考下为什么要引入SI-Finder模块?理论基础来源于Distributed Source Coding(DSC),是视频压缩中的常见方法,其要求编码端与恢复端保持一一对应关系。例举论文中阐述的例子,假设X、Y为对应的两个patch且满足||X-Y||<=3. 我们可以将X压缩至满意的bits,然后根据X、Y之间的对应关系,在解码端通过Y传达的信息,快速找到并恢复想要的X。
所以SI-Finder模块就是用来解决这个X、Y对应关系的存在,细节如下:
可以发现,Xdec和Y并不构成一一对应关系,SI-Finder模块会对Y进行auto-encoder处理得到Ydec,然后对Xdec小块与Ydec小块(patch_size)进行互相关性计算(上式所示),从而得到X在Ydec中的对应位置。将Ydec中的位置信息映射至Y中,即得到我们想要的X/Y对应关系,获得Ysyn信号。最后,Ysyn信号与Xdec信号进行concatenated并输入SI-Net模块进行图像恢复。
来看一下算法的损失函数:
同样也是失真率和压缩率的trad-off,需要注意的是,算法仅对
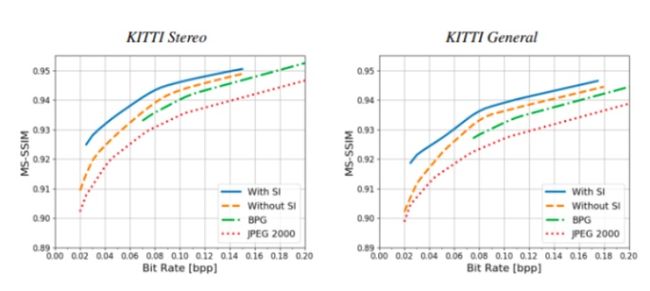
Results
另外的,论文还针对是否使用2D Gaussian mask处理side information 进行了对比实验,这里不展开描述了。总体来看,算法思路较清晰直观,也给出了开源代码[4],值得好好学习思考~ 以上,如理解有误还请批评指正~
[1] DENSITY MODELING OF IMAGES USING A GENERALIZED NORMALIZATION TRANSFORMATION
[2] Variational image compression with a scale Hyper-prior
[3] Scale mixtures of gaussians and the statistics of natural images
[4] ayziksha/DSIN
适合于图像重建问题的归一化层:GENERALIZED NORMALIZATION TRANSFORMATION(GDN)
拉格朗日中值定理:PCS2016、ICLR2016、2017、2018论文阅读
深度学习图像压缩_1-概述:自编码器、量化、熵编码、率失真_heweiqiran的博客-CSDN博客_深度学习 图像压缩
详解EM算法与混合高斯模型(Gaussian mixture model, GMM)
熵编码_百度百科
边缘分布_百度百科