Python入门到实战（八）Jupyter Notebook路径修改、数学基础：分段函数、矩阵运算、微积分、概率与统计、蒙特卡洛近似算法、线性回归、逻辑运算补充

Jupyter Notebook工作路径修改

Anaconda下修改

未修改是是默认为HOMEPATH，也就是进入C盘用户文件夹下

修改路径方式为，找到

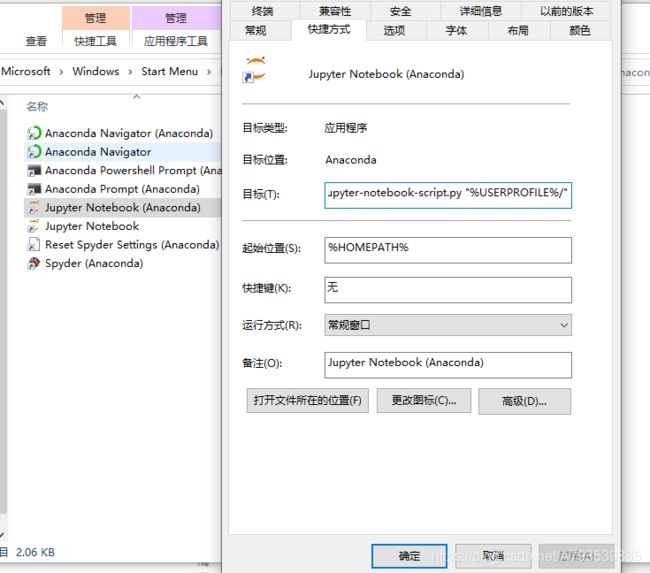
右键属性后，修改目标中的%USERPROFILE%和起始位置为：C:\sourceCode\python\jupyter_notebook

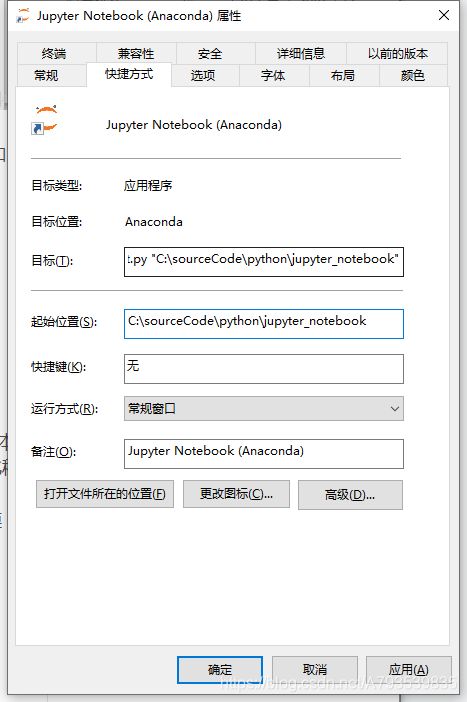
之后重启Jupyter Notebook就会发现路径已经修改成功

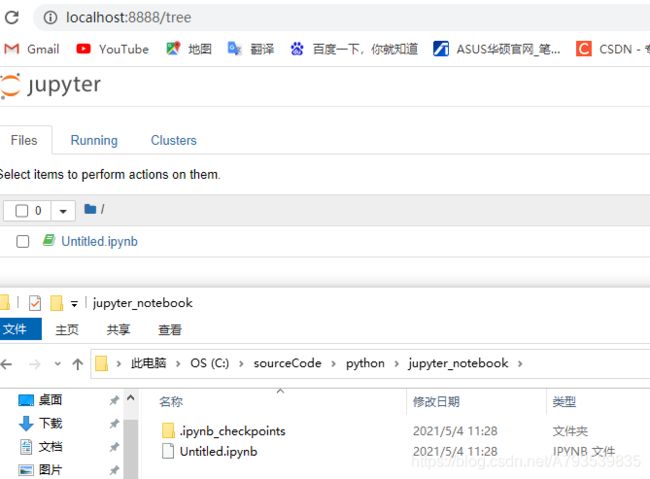
未使用Anaconda下修改

WIN10系统找到C:\Users\Username\.jupyter下的jupyter_notebook_config.py，使用记事本打开后找到
# c.NotebookApp.notebook_dir = ' '
修改为c.NotebookApp.notebook_dir = 'C:\sourceCode\python\jupyter_notebook'
CTRL+S保存后重启Jupyter Notebook

数学基础知识应用题：

本文中使用Anaconda中的Jupyter Notebook。其本质是一个 Web 应用程序，便于创建和共享文学化程序文档，支持实时代码，数学方程，可视化和 markdown。用途包括：数据清理和转换，数值模拟，统计建模，机器学习等等。

分段函数

-梯度电费计算

题目：
某城市的居民用电的收费方式如下
• 10度以内：固定10元
• 10-50度的部分：每度0.538元
• >50度的部分: 每度0.752元
请用代码搭建函数，计算用电5.56
度、30.21度、100.82度时候的成本

代码

def check_elc(ini):
    #10度以内10元
    if ini<0:
        print("error!")
        money=0
    elif ini<10:
        money = 10
    #10-50度部分，每度0.538元
    elif ini>10 and ini<50:
        money = 10+ (ini-10)*0.538
    #>50度，每度0.752
    else:
        money=10+0.538*40+0.752*(ini-50)
    return money

#计算5.56度,30.21度，100.82度
print('-1度金额：',check_elc(-1))
print('5.56度金额：',check_elc(5.56))
print('30.21度金额：',check_elc(30.21))
print('100.82度金额：',check_elc(100.82))

error!
-1度金额： 0
5.56度金额： 10
30.21度金额： 20.872980000000002
100.82度金额： 69.73664

矩阵运算

-计算每家店应收取的费用：

总店往2家分店（编号1、2）发送3种商品（苹果，猪肉和纸巾），用矩阵运
算来计算向每家分店收取的费用。

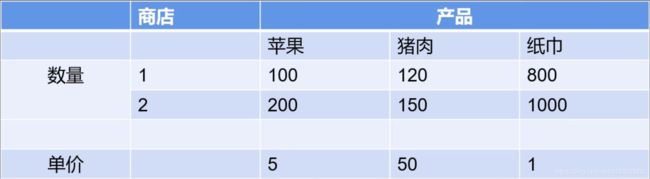
代码：

import numpy as np
num=np.array([[100,120,800],[200,150,1000]])
pri=np.array([[5],[50],[1]])
res=np.dot(num,pri)
print(res)

[[7300]
 [9500]]

微积分

-算积分面积

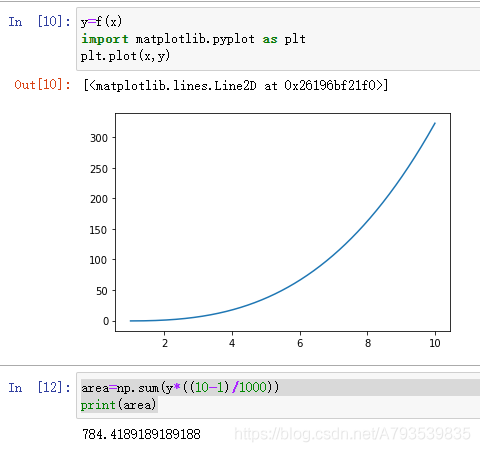
计算y=1/3(x^3)-x 从x=1到x=10与x轴形成的区域面积：

代码：

import numpy as np
def f(x):
    return 1/3*x**3-x
x=np.linspace(1,10,1000)
y=f(x)
import matplotlib.pyplot as plt
plt.plot(x,y)
area=np.sum(y*((10-1)/1000))
print(area)

结果：

概率与统计

-题目1 生成平均值为0，标准差为1的10000个正

态分布的随机数
生成平均值为0，标准差为1的10000个正
态分布的随机数，统计数值>0,>0.5,>1,>2的
随机数个数

代码

import numpy as np
#均匀分布
np.random.rand(10000)
#高斯分布
np.random.randn(10000)
tmp=np.random.randn(10000)
print(tmp)

[ 1.28655249 -1.93790531  1.79859047 ...  0.62670699  0.06486803
  0.63654665]

print(np.sum(tmp>0))

5015

print(np.sum(tmp>0.5))

3055

print(np.sum(tmp>1))

1547

print(np.sum(tmp>2))

241

上述结果其实完全符合正态分布

-题目2 蒙特卡罗近似算法

蒙特卡罗近似算法：在边
长为1正方形区间内随机落点，
问落点在绿色四分之一圆区
间内的概率是多少？

代码

生成二维的均匀分布的随机数

dots=np.random.rand(10000,2)
print(dots)

[[0.55609015 0.30476082]
 [0.1759479  0.62571909]
 [0.82501276 0.52693109]
 ...
 [0.65862453 0.64640773]
 [0.24278743 0.04102342]
 [0.18313591 0.75660603]]

其中最大值，观察是非常接近1的

np.max(dots)

0.9999928092943885

其中最小值也是十分接近于0的

np.min(dots)

3.658261018757436e-05

这时根据x,y坐标即可算出半径。若是半径小于1 ，则判定为在1/4圆区内

radius=np.sqrt(dots[:,0]**2+dots[:,1]**2)
print(radius)

[0.6341257  0.64998618 0.97892923 ... 0.92283759 0.24622887 0.77845453]

print(np.sum(radius<=1))

7815

统计出个数有7815个，总样本数为10000，大约占了0.78的面积，同下用公式算的的结果相差无几。若是想要更逼近，则采取极限思想，点打的越密，例如取10000000个，精度便会更高…

print(np.pi/4)

0.7853981633974483

线性回归

回归：根据已有的数据，建立因变量Y与自变量X的定量（函数）关系的模型
当新自变量出现，可以对应取出因变量值做出预测

·题目

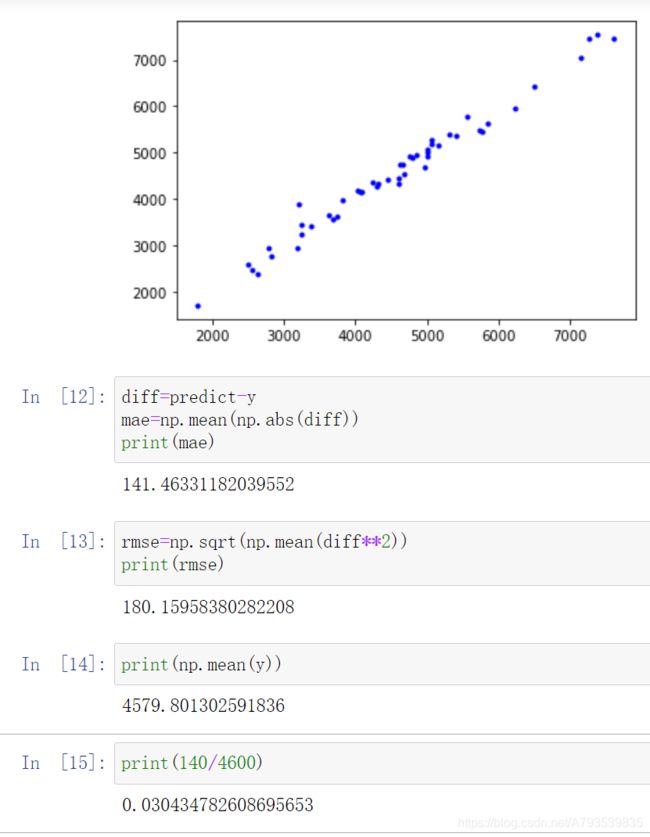
在某小区抽样调查获得家庭 月收入，家庭人数，家庭每 月食品支出的调查数据，请 过通过线性回归建立家庭月 收入，家庭人数为自变量， 每月食品支出为因变量的多元线性回归模型

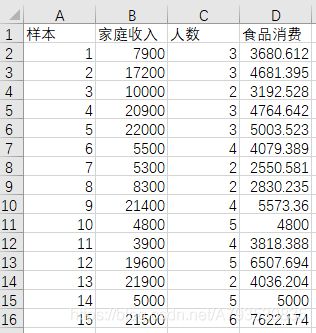
代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import sklearn
data=pd.read_csv("data.csv")
data=data.values #data[key].values 类型是numpy 的ndarray类型的数据
x=data[:,1:3]
y=data[:,3]
from sklearn.linear_model import LinearRegression
model=LinearRegression()
model.fit(x,y) #学习
predict=model.predict(x) #预测
plt.plot(y,predict,".b")#画出以y为x轴与y^（预测结果）为y轴的图形

逻辑运算

逻辑运算优先顺序（补充笔记一内置对象中逻辑运算）

从高往低排列
括号内的运算（）
指数（** ^）
乘（*）、除（/）、取模（%）、取整（//）
加（+），减（-）
比较运算符（> < >= <=）
比较运算符（== !=）
逻辑运算符（and or not）

例题

1. 1+5*3 and (3>4 or (not True))
2. (1+1)/2>3 or (1+2)*(4/2)

答案：
1.False
2.True