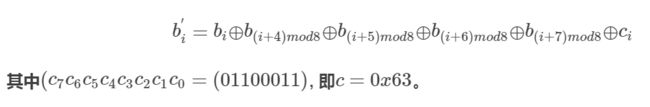作业要求如下:
- 使用Python或者Sage语言;
- 上交电子版,用MD书写,提交网络链接即可;比如,使用jianshu、github、作业部落或者CSDN等;
- 代码需具有可读性和可验证性(比如,可容易让审阅者知道所生成的S-box的正确性。)
任务一:
任意给定两个素数p和q,p!= q,记 N = p * q ,构造Zn*.
问题(编程解决):
- 是否每个元素都有inverse?是否成群?
- 这个集合有多少元素?
Python源代码
- 判断是否为素数
def isprime():
count = 1
while (count):
n = int(input("输入一个质数:"))
for i in range(2, n):
if n % i == 0:
print(" %d 这不是一个质数!" % n)
break
else:
return n
- 生成一个与N互素的列表
def CommonFactor(a,b):
if a
- 判断是否存在逆元
def is_inverse(list,n):
mark=1
for i in range(0,len(list)):
count=1
for j in range(0,len(list)):
if((list[i]*list[j])%n==1):
count = 0
print("%s存在逆元%s"%(list[i],list[j]),end=" ")
if count:
print("%s不存在逆元"%(list[i]),end=" ")
mark=0
print()
if(mark):
print("任何元素都有逆元")
return mark
- 判断运算是否封闭
def is_closed(list,n):
mark=1
for i in range(0, len(list)):
for j in range(0, len(list)):
count=0
for k in range(0, len(list)):
if((list[i]*list[j])%n == list[k]):
count=1
num=list[k]
if count:
print("%s*%s封闭值为%s"%(list[i],list[j],num))
else:
print("%s*%s不封闭"%(list[i],list[j]))
mark=0
return mark
- 主函数
def main():
p=isprime()
count=1
while(count):
q=isprime()
if not q==p:
count=0
else:
print("与第一个质数相同,请重新输入")
n=p*q
list=[]
for i in range(1,n):
k=CommonFactor(i,n)
if k==1:
list.append(i)
for i in range(0,len(list)):
print(list[i],end=" ")
print()
a=is_inverse(list,n)
b=is_closed(list,n)
if a==1 and b==1:
print("任意元素都有逆元且运算封闭,成群")
print("群元素有%s个"%(len(list)))
elif a==0:
print("存在元素没有逆元,不成群")
elif b==0:
print("运算不封闭,不成群")
main()
任务二
写一个程序,实现AES的S-box的构造。
整体实现思路
- 初始化S-box,使第x行第y列的元素为{xy}。
(代码实现时这一步和第二步合在一个initialize()函数中完成)
- 对S-box中的每个元素求乘法逆元
(求乘法逆元用到扩展欧几里得算法,所以必须要实现GF( 2^8 )中的乘法运算)
-
对S-box中的公式运用一下公式得到最终的S-box。
源代码
#include
#include
#include
using namespace std;
unsigned char exp[256], log[256], inv[256];
unsigned char GFmul(unsigned char a, unsigned char b){
//GF(2^8) 乘法
unsigned char result = 0;
if((b&1) == 1)result = a;
b >>= 1;
for(int i = 1; i < 8; i ++){
if(a > 127){
a = (a << 1) ^ 0x1b;
}
else{
a <<= 1;
}
if((b&1) == 1){
result ^= a;
}
b >>= 1;
}
return result;
}
void generateMulTab(){
//选择生成元3作为构造乘法表的基础
const int N = 3;
exp[1] = N;
log[N] = 1;
unsigned char tmp = N;
for(int i = 2; i < 256; i ++){
tmp = GFmul(tmp, N);
exp[i] = tmp;
log[tmp] = i;
}
}
void generateMulInverse(){
//利用exp来构造乘法逆元
inv[0] = 0;
inv[1] = 1;
//若3^m * 3^n = 1 = 3^255,则 m + n = 255
for(int i = 1; i < 255; i ++){
inv[exp[i]] = exp[255-i];
}
}
unsigned char SBoxValue(unsigned char x){
//返回SBOX对应的值
bool xb[8];
unsigned char y = inv[x];
//AES规定的常数项
const bool N[8][8] = {1, 0, 0, 0, 1, 1, 1, 1,
1, 1, 0, 0, 0, 1, 1, 1,
1, 1, 1, 0, 0, 0, 1, 1,
1, 1, 1, 1, 0, 0, 0, 1,
1, 1, 1, 1, 1, 0, 0, 0,
0, 1, 1, 1, 1, 1, 0, 0,
0, 0, 1, 1, 1, 1, 1, 0,
0, 0, 0, 1, 1, 1, 1, 1};
const bool C[8] = {1, 1, 0, 0, 0, 1, 1, 0};
//将y转化为数组用作矩阵运算
for(int i = 0; i < 8; i ++){
xb[i] = (y&1);
y >>= 1;
}
//矩阵乘法
bool tmp[8];
for(int i = 0; i < 8; i ++)tmp[i] = 0;
for(int i = 0; i < 8; i ++){
for(int j = 0; j < 8; j ++){
tmp[i] ^= (N[i][j] & xb[j]);
}
tmp[i] ^= C[i];
}
//将数组结果转化为数值
unsigned char result = 0;
result |= tmp[7];
for(int i = 6; i >= 0; i --){
result <<= 1;
if(tmp[i])result |= 1;
}
return result;
}
int main(){
//单元测试,输出SBOX的全部值
generateMulTab();
generateMulInverse();
unsigned char SBox[16][16];
for(int i = 0; i < 16; i ++){
for(int j = 0; j < 16; j ++){
unsigned char tmp = i*16 + j;
SBox[i][j] = SBoxValue(tmp);
}
}
ofstream write("Test.txt");
for(int i = 0; i < 16; i ++){
for(int j = 0; j < 16; j ++){
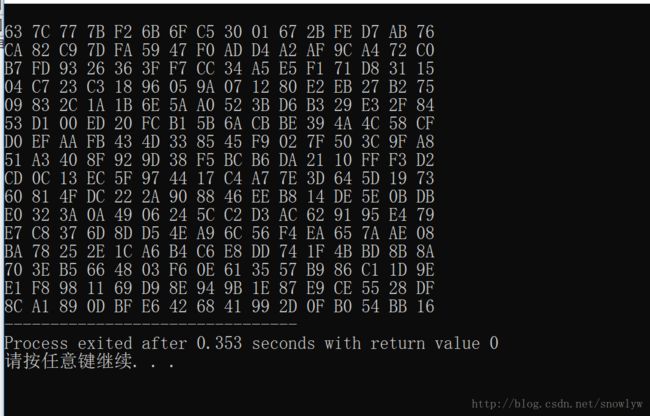
write<
运行结果