基于SVM,KNN,CNN的数字图像识别
文章目录
- 一些瞎扯的话
- 一、必备的有关 OpenCV 和 HOG 的前置知识
-
- 1.关于OpenCV模块:图片读、写和显示操作,以及图片属性
- 2.关于OpenCV模块:图片缩放和仿射变换
- 3.有关 HSV 空间, Gramma变换, HOG 特征的知识。
- 二、用 OpenCV 的仿射变换实现图片缩放
- 三、理解 HOG、ORC 过程,使用SVM 和 KNN 模型实现数字图像的识别
-
- 1.数字图像的类型
- 2.提取数字图像的HOG特征
- 3.训练模型并测试
- 四、使用 CNN 神经网络模型实现数字图像的识别
-
- 1.处理图像数据
- 2.设置模型,训练模型
- 3.保存模型
- 4.测试模型
- 五、代码总和
-
- 1.图片缩放
- 2.使用 SVM 和 KNN 模型实现数字图像识别
- 3.使用 CNN 模型实现数字图像识别
一些瞎扯的话
跟朋友们随便瞎扯几句
在学校过了个五一,也没回家也没出去玩,倍感无聊和寂寞。看着空间里大家晒出游,晒朋友,更加难受,我想,不能这样了。于是我打开老师布置的作业开始研究,实验搞了一天,写文档又写了一天,写完后感觉十分充实,快乐了许多。果然“学习使人快乐”所言非虚哈哈哈。
以上内容纯属瞎扯,写着作业还是寂寞呜呜呜。
这里推荐Todd Li翻唱的一首歌《最寂寞的时候》
离谱的是布置完实验的第二天就有粉丝催更,我看明白了,你们根本不馋我身子,只馋我代码。

一、必备的有关 OpenCV 和 HOG 的前置知识
想要看懂下面的实验,这些知识必不可少。
1.关于OpenCV模块:图片读、写和显示操作,以及图片属性
(1)读入图片:
读入图片时使用’cv.imread’函数,第一个参数是图片位置,第二个参数是读图片的模式,‘1’为读入为彩色图像,‘0’为读入为灰度图像,’-1’为原始图像读入。因此将彩色图像转为灰度图时,只需选择参数为‘0’即可。
代码如下(示例):
import cv2 as cv
if __name__ == '__main__':
# 读图片(有多种模式)
# Load an color image in grayscale
img = cv.imread('1.jpg', 0)
# 1 彩色 0 灰度图像 -1 原始图像
(2)写图片:
写图片时直接使用‘cv.imwrite’函数即可,第一个参数为写入的位置,第二个参数即图像本身。如(1),笔者读入’1.jpg’,读入时转为灰度图像,在写入同一文件夹下的’1_grey.jpg’文件中。两张图片如下如所示:
代码如下(示例):
cv.imwrite('1_grey.jpg', img)
(3)显示图片:
显示图片是使用‘cv.imshow’函数,第二个参数是要显示的图像,第一个参数是显示时图片窗口的名字。注意显示图片时要加上一行’cv.waitKey(0)’来让窗口等待用户按键,不然显示的图片会一闪而过。
代码如下(示例):
# 显示图片
cv.imshow('picture1', img) # 第一个参数定义窗口名
cv.waitKey(0) #无限制的等待用户的按键
cv.destroyAllWindows()
(4)图片属性:
图片属性包括高度、宽度、通道数、像素总数等信息,示例如下图:

2.关于OpenCV模块:图片缩放和仿射变换
(1)图片缩放:
使用 OpenCV 模块实现图片缩放时主要使用 ‘cv2.resize’函数,注意是‘主要’,因为仿射变换也能实现图片缩放,下面一个实验即是。
函数可以使用参数 ‘fx’和‘fy’或者直接使用‘dsize’参数来控制缩放比例,十分方便。

代码如下(示例):
smaller = cv.resize(img, None, fx=0.5, fy=0.5, interpolation=cv.INTER_CUBIC) # OR
height, width = img.shape[:2]
bigger = cv.resize(img, (int(1.2 * width), int(1.2 * height)), interpolation=cv.INTER_CUBIC)
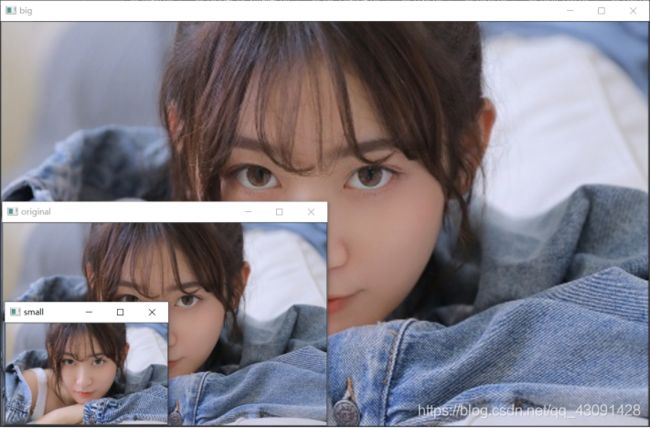
结果示例如下,注意看窗口名字来辨别图片:
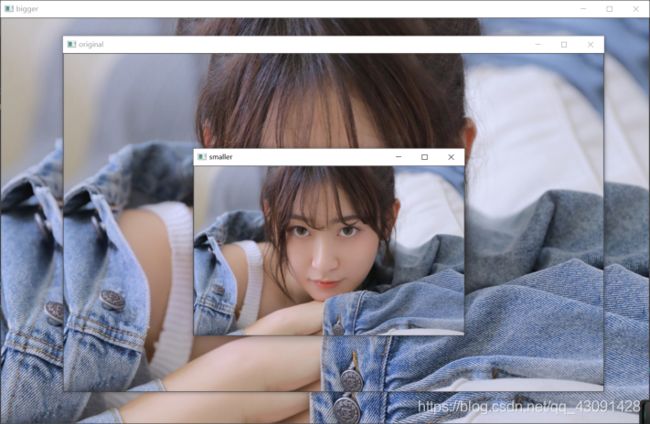
(2)仿射变换:
一个任意的仿射变换都能表示为乘以一个矩阵(线性变换)接着再加上一个向量(平移)。
旋转(线性变换)
平移 (向量加)
缩放操作 (线性变换)
我们通常使用 2 x 3 矩阵来表示仿射变换.其中左边的2×2子矩阵是线性变换矩阵,右边的2×1的两项是平移项:

对于图像上的任一位置(x,y),仿射变换执行的是如下的操作:

平移:将每一点移到到(x+t , y+t),变换矩阵为:

旋转变换:目标图形围绕原点顺时针旋转Θ弧度,线性变换矩阵为:
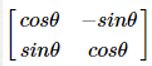
目标图形以(x,y)为轴心顺时针旋转θ弧度,相当于两次平移与一次原点旋转变换的复合,即先将轴心(x,y) 移到到原点,然后做旋转变换,最后将图片的左上角置为图片的原点。变换矩阵为:

仿射函数‘cv2.warpAffine’:

用来获得变换矩阵M的函数‘cv2.warpAffine’,方便我们在进行图片旋转时计算弧度:

仿射函数‘cv.getAffineTransform’:

看懂了吗,建议看不懂的童鞋重新研读线性代数课本

3.有关 HSV 空间, Gramma变换, HOG 特征的知识。
(1)HSV 空间:
HSV空间是由美国的图形学专家A. R. Smith提出的一种颜色空间,HSV分别是色调(Hue),饱和度(Saturation)和明度(Value)。
在HSV空间中进行调节就避免了直接在RGB空间中调节是还需要考虑三个通道的相关性。OpenCV中H的取值是[0, 180),其他两个通道的取值都是[0, 256),通过HSV空间对 图像进行调色更加方便:
转换图片制式的函数‘cv2.cvtColor’:

转换类型表:
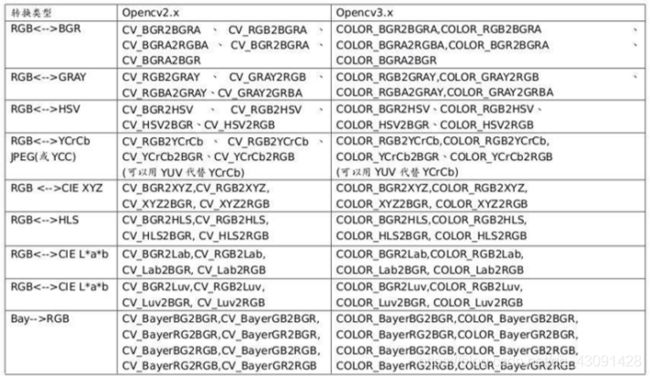
(2)Gramma变换:
Gamma变换是矫正相机直接成像和人眼感受图像差别的一种常用手段,简单来说就是通过非线性 变换(因为人眼对自然的感知是非线性的)让图像从对曝光强度的线性响应变得更接近人眼感受到 的响应。Gamma压缩公式:
![]()
如果直方图中的成分过于靠近0或者255,可能就出现了暗部细节不足或者亮部细节丢失的情况。一个常用方法是考虑用Gamma变换来提升/降低暗部细节。
示例图如下:
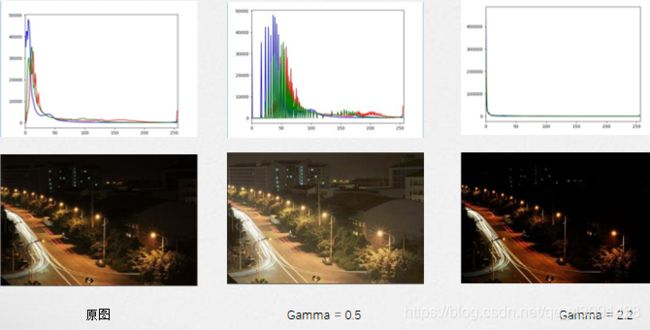
(3)HOG 特征:
方向梯度直方图(Histogram of Oriented Gradient, HOG)特征是一种在计算机视觉和 图像处理中用来进行物体检测的特征描述子。它通过计算和统计图像局部区域的梯度方向直方 图来构成特征。HOG特征结合SVM分类器已经被广泛应用于图像识别中,尤其在行人检测中获 得了极大的成功。
HOG特征提取方法就是将一个image(你要检测的目标或者扫描窗口):
1)灰度化(将图像看做一个x,y,z(灰度)的三维图像);
2)采用Gamma校正法对输入图像进行颜色空间的标准化(归一化);目的是调节图 像的对比度,降低图像局部的阴影和光照变化所造成的影响,同时可以抑制噪音的干扰;
3)计算图像每个像素的梯度(包括大小和方向);主要是为了捕获轮廓信息,同时进一步弱化光照的干扰。
4)将图像划分成小cells(例如10X10像素/cell);
5)统计每个cell的梯度直方图(不同梯度的个数),即可形成每个cell的descriptor;
6)将每几个cell组成一个block(例如2*2个cell/block),一个block内所有cell的特征descriptor串联起来便得到该block的HOG特征descriptor。
7)将图像image内的所有block的HOG特征descriptor串联起来就可以得到该image(你要检测的目标)的HOG特征descriptor了。这个就是最终的可供分类使用的特征向量了。
这里只是简单讲一下提取 HOG 特征的步骤,具体操作见下面实验。
二、用 OpenCV 的仿射变换实现图片缩放
我们通常使用 2 x 3 矩阵来表示仿射变换.其中左边的2×2子矩阵是线性变换矩阵,右边的2×1的两项是平移项:

对于图像上的任一位置(x,y),仿射变换执行的是如下的操作:

我们要实现缩放,并不需要对图像进行平移,B矩阵中的值取0即可。接下来我们考虑怎么使用A矩阵实现缩放。
根据线性代数的知识,我们可以取a00和a11为0,取a01和a10相等,这样的话图像相当于没有旋转,而且每个像素点的横纵坐标都乘以了一个相同的值。设a01和a10的值为rate,乘以A矩阵之后,每个像素点的位置由(x, y)移到了(x*'rate, y*rate),即实现了缩放。
代码如下:
import numpy as np
import cv2 as cv
# Load an color image in grayscale
img = cv.imread('11.jpg')
rows, cols = img.shape[:2]
#缩放
rate = 0.5
np1 = np.float32([[rate, 0, 0], [0, rate, 0]])
dst4 = cv.warpAffine(img, np1, (int(cols*rate), int(rows*rate)))
rate = 2
np2 = np.float32([[rate, 0, 0], [0, rate, 0]])
dst5 = cv.warpAffine(img, np2, (int(cols*rate), int(rows*rate)))
cv.imshow('original',img)
cv.imshow('small',dst4)
cv.imshow('big',dst5)
cv.waitKey(0) # 无限制的等待用户的按键
cv.destroyAllWindows()
三、理解 HOG、ORC 过程,使用SVM 和 KNN 模型实现数字图像的识别
本实验的难点到了。
本实验的步骤十分简单,可以分为两个部分,提取数字图像的HOG特征,和放到分类器中进行训练分类。
1.数字图像的类型
本次实验的数据集分为训练集和测试集两个部分,每一部分都包含十个文件夹,分别存有一定数量的数字图像,文件夹名称即是储存的数字图像中的数字。
训练集共包含10000张图片,测试集共包含5000张图片。每张图片的大小是28*28,与MNIST数据集图片相同。

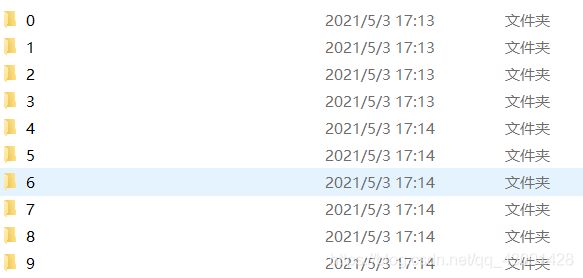
2.提取数字图像的HOG特征
在前置知识中提到了提取图像 HOG 特征的步骤,下面是具体实现。
(1)读入图像
读取训练集和测试集中的每个图像,定义images列表存储图像的HOG特征,lables列表存储图像的分类。最后用numpy模块将列表转化为矩阵,以用于模型训练。
在读入图像时,首先要转化为灰度图像,之后进行偏斜校正,提取HOG特征值,降维等操作,下面来一一详解。
def data(path):
images = []
lables = []
indexs = os.listdir(path)
for index in indexs:
names = os.listdir(path + '\\' + index)
for name in names:
image_path = path + '\\' + index + '\\' + name
img = cv2.imread(image_path, 0)#灰度化
img_deskew = deskew(img)#偏斜校正
img_hsv = hog.compute(img_deskew)
images.append(np.squeeze(img_hsv))
lables.append(int(index))
return np.array(images), np.array(lables)
(2)偏斜校正
先解释一下矩特征:
从图像中计算出来的矩通常描述了图像不同种类的几何特征如:大小、灰度、方向、形状等,图像矩广泛应用于模式识别、目标分类、目标识别与防伪估计、图像编码与重构等领域。矩是概率与统计中的一个概念,是随机变量的一种数字特征。opencv中提供了moments()来计算图像中的中心矩(最高到三阶)。Opencv中的moments得到图像矩的字典,包括m00,m10,m01,m20,m11,m02,m30,m21,m12,m03,mu20,mu11,mu02,mu30,mu21,mu12,mu03,nu20,nu11,nu02,nu30,nu21,nu12,nu03。
也就是说调用‘cv.moments’函数,就能自动计算出图片的中心距。这里数字图像我们视为矩形,我们主要使用图片的二阶矩(mu02)判断图像中数字的方向。
代码如下,SZ为图片的长和宽。我们先利用‘cv2.threshold’函数对图片(传入函数的为灰度图)进行二值化处理,将大于等于127的值全改为255,小于127的值全改为0。该函数返回的第一个值就是输入的thresh值,第二个就是处理后的图像。
再利用‘cv2.findContours’函数来查找图像的轮廓,函数第一个参数是寻找轮廓的图像;第二个参数表示轮廓的检索模式,第三个参数method为轮廓的近似办法,这里不再详细说明。
‘cv2.findContours’函数返回两个值,一个是轮廓本身,还有一个是每条轮廓对应的属性。
我们利用计算出的轮廓,运用‘cv2.moments’函数计算图片的二阶矩,再进行判断,如果其小于0.01,认为图像没有偏斜,直接返回原图像。
否则利用仿射变换进行校正。
def deskew(img):
SZ = 28
ret, thresh = cv2.threshold(img, 127, 255, 0)
contours, hierarchy = cv2.findContours(thresh, 1, 2)
cnt = contours[0]
m = cv2.moments(cnt)
if abs(m['mu02']) < 1e-2:
# no deskewing needed.
return img.copy()
# Calculate skew based on central momemts.
skew = m['mu11']/m['mu02']
# Calculate affine transform to correct skewness.
M = np.float32([[1, skew, -0.5 * SZ * skew], [0, 1, 0]])
# Apply affine transform
img = cv2.warpAffine(img, M, (SZ, SZ), flags=cv2.WARP_INVERSE_MAP | cv2.INTER_LINEAR)
return img
(3)计算水平和垂直梯度
可以通过使用以下内核卷积图像来轻松实现。左下图为大小为1的内核,mag为梯度大小,ang为梯度方向的角度的弧度值。

(4)计算梯度分布的直方图,梯度被分为9等分
以一个8*’8的cell为例,下图为RGB颜色向量的长度和方向的矩阵。我们将方向从0-180九等分,对于一个颜色向量的长度,我们根据其方向将其分在两个最近的梯度值上。对于一个cell中的每个像素点执行此操作,即可得到该cell的梯度分布直方图。
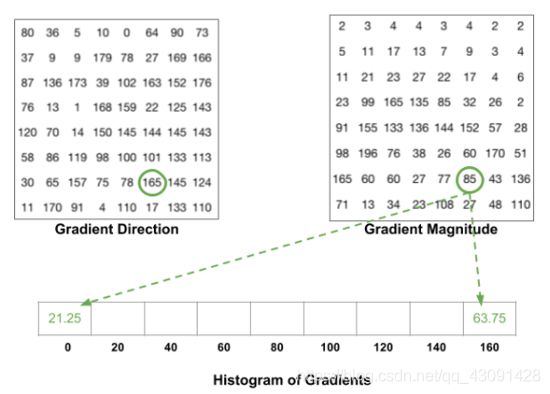
(5)向量归一化
在上一步中,我们基于图像的梯度创建了一个直方图。 图像的渐变对整体光照敏感。 如果通过将所有像素值除以2来使图像更暗,则梯度大小将改变一半,因此直方图值将改变一半。
理想情况下,我们希望描述符与照明变化无关。 换句话说,我们想“标准化”直方图,以使它们不受光照变化的影响。在解释如何对直方图进行归一化之前,让我们看看如何对长度为3的向量进行归一化。
假设我们有RGB颜色向量[128,64,32]。 此向量的长度为sqrt {128 ^ 2 + 64 ^ 2 + 32 ^ 2} = 146.64。 这也称为向量的L2范数。 将该向量的每个元素除以146.64,得出的归一化向量为[0.87,0.43,0.22]。
现在考虑另一个向量,其中元素是第一个向量的值的两倍2*[128,64,32] = [256,128,64]。 标准化[256,128,64]将产生[0.87,0.43,0.22],这与原始RGB向量的标准化版本相同。光照大小将不影响向量值。
(6)将向量分布直方图拼接并展开,得到最后的HOG特征值
(7)代码实现:
下面以(20,20)大小的图像为例,以(10,10)大小计算梯度分布直方图,Normalize大小也为(10,10)。
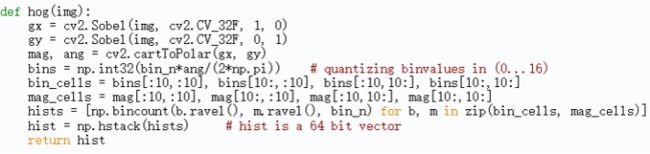
除了上述代码,我们也可以使用opencv自带的HOGDescriptor计算HOG特征值,调节winSize,blockSize等参数获得更好的效果。(本实验中笔者用的这种方法)
winSize = (28, 28)
blockSize = (14, 14)
blockStride = (7, 7)
cellSize = (14, 14)
nbins = 9
derivAperture = 1
winSigma = -1
histogramNormType = 0
L2HysThreshold = 0.2
gammaCorrection = 1
nlevels = 64
signedGradients = True
hog = cv2.HOGDescriptor(winSize, blockSize, blockStride,
cellSize, nbins, derivAperture,
winSigma, histogramNormType, L2HysThreshold,
gammaCorrection, nlevels, signedGradients)
这里是对各种参数的描述:
winSize:数字图像的大小为28×28,此处为整个图像计算一个描述符。
cellSize:图像是28×28灰度图像。换句话说,图像由28×28 = 784个像素点表示。cellSize是根据对分类重要的特征的比例来选择的。一个很小的cellSize会使特征向量的大小过大,而一个很大的cellSize可能无法捕获相关信息。这里我们选择了14×14的cellSize,可以尝试修改cellSize获得更好的效果。
blockSize:用于解决亮度变化影响gradient分布。较大的块大小会使本地像素变化的重要性降低,而较小的块大小会使本地像素变化的权重更大。通常,blockSize设置为2 x cellSize,因为在我们的数字分类图像中,亮度并不是很大的干扰项。因此14×14的块大小给出了最佳结果。
blockStride:blockStride确定相邻块之间的重叠并控制对比度归一化的程度。通常,将blockStride设置为blockSize的50%。
nbins:nbins设置渐变直方图中的bin数。 HOG论文的作者建议值为9,以20度为增量捕获0到180度之间的梯度。
signedGradients:通常,渐变可以具有0到360度之间的任何方向。这些梯度称为“有符号”梯度,与“无符号”梯度相反,“无符号”梯度使符号下降并采用0到180度之间的值。
3.训练模型并测试
(1) 获得训练数据和测试数据
直接使用上述data函数保存训练数据和测试数据,并打印出数据的大小。
这里要注意,训练数据和测试数据的维度应该均为2,且第一个维度为数据的数量。因此在data函数中加了一行降维代码“np.squeeze(img_hsv)”,将81*1的二维矩阵降维为一维矩阵。
train_data, train_lable = data('digit_data\\train')
print(train_data.shape)
images_test, lables_test = data('digit_data\\test')
print(images_test.shape)
![]()
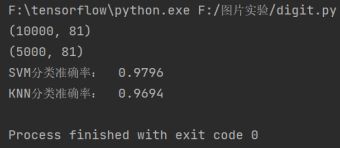
打印结果如下:

(2) 训练SVM模型并进行测试
直接带入SVM模型训练和测试模板即可。
clf = make_pipeline(StandardScaler(), SVC(gamma='auto'))
clf.fit(train_data, train_lable)
result = clf.predict(images_test)
correct = np.sum(result == lables_test)
print('SVM分类准确率: ', correct/len(images_test))
(3) 训练KNN模型并进行测试
同上:
neigh = KNeighborsClassifier(n_neighbors=3)
neigh.fit(train_data, train_lable)
result = neigh.predict(images_test)
correct = np.sum(result == lables_test)
print('KNN分类准确率: ', correct/len(images_test))
四、使用 CNN 神经网络模型实现数字图像的识别
1.处理图像数据
使用 CNN 模型时,我们不需要提取 HOG 特征,只需灰度化即可。
def data(path):
images = []
lables = []
indexs = os.listdir(path)
for index in indexs:
names = os.listdir(path + '\\' + index)
for name in names:
image_path = path + '\\' + index + '\\' + name
img = cv2.imread(image_path, 0)
images.append(np.array(img))
lables.append(index)
return np.array(images), np.array(lables)
将图片读入矩阵之后,进行归一化操作,除于255。再对矩阵升维,由三维升为四维。
另外还要对分类标签进行one-hot编码。
if __name__ == "__main__":
x_train, y_train = data('digit_data\\train')
x_test, y_test = data('digit_data\\test')
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train = x_train / 255.0
x_test = x_test / 255.0
x_train = x_train.reshape(x_train.shape[0], 28, 28, 1)
y_train = keras.utils.to_categorical(y_train, 10)
x_test = x_test.reshape(x_test.shape[0], 28, 28, 1)
y_test = keras.utils.to_categorical(y_test, 10)
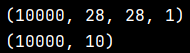
print (x_train.shape)
print (y_train.shape)
2.设置模型,训练模型
CNN框架图如下:
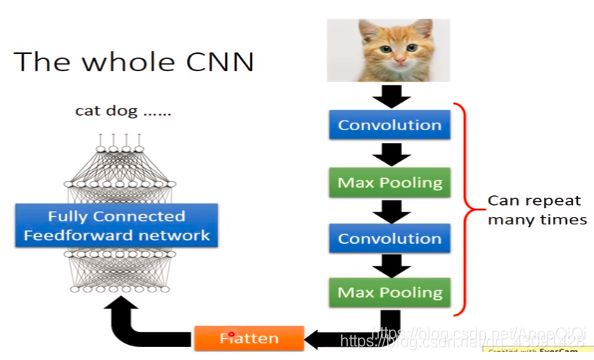
简单来说,卷积层用来提取特征,而池化层可以减少参数数量。
pooling池化的作用则体现在降采样:保留显著特征、降低特征维度,增大kernel的感受野。另外一点值得注意:pooling也可以提供一些旋转不变性。
实验中我们使用两对卷积、池化层。
我们设置卷积核为大小为5*5,第一层卷积层使用32个卷积核,第二层卷积层使用64个卷积核。
Padding选择补0使得卷积后的激活映射尺寸不变。
激活函数我们使用‘relu’。
池化层我们使用最大池化(Max Pooling),取一个区域内所有神经元的最大值。
最后添加两个全连接层。设置损失函数,评估标准后,模型设置完毕。
使用 ‘model.fit’进行模型训练。
#build the model
model = Sequential()
model.add(Conv2D(32,(5,5),activation = 'relu',input_shape = (28,28,1),padding='same'))
model.add(MaxPooling2D(pool_size = (2,2)))
model.add(Conv2D(64,(5,5),activation = 'relu',padding='same'))
model.add(MaxPooling2D(pool_size = (2,2)))
model.add(Flatten())
model.add(Dense(1024,activation = 'relu'))
model.add(Dense(10,activation = 'softmax'))
sgd = optimizers.SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True)
model.compile(loss=keras.losses.categorical_crossentropy,optimizer=sgd,metrics=['accuracy'])
model.fit(x_train, y_train, batch_size = 100, epochs = 14)
3.保存模型
使用 ‘model.save_weights’ 保存模型的权重;使用’model.load_weight’加载模型的权重。
训练模型时注释掉加载模型的代码;
加载模型时注释掉‘model.fit’训练模型和‘model.save’保存模型权重的代码。
# save architecture
model.save_weights('CNN_model')
#load
#model.load_weights('cnn_model')
4.测试模型
使用测试集进行模型的测试,输出测试结果。
score = model.evaluate(x_test, y_test)
print ("loss: "+str(score[0]))
print ("accuracy: "+str(score[1]))
五、代码总和
1.图片缩放
前面放过完整代码了,大家动动手去前面翻一下
2.使用 SVM 和 KNN 模型实现数字图像识别
from sklearn.svm import SVC
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
import os
import cv2
import numpy as np
winSize = (28, 28)
blockSize = (14, 14)
blockStride = (7, 7)
cellSize = (14, 14)
nbins = 9
derivAperture = 1
winSigma = -1
histogramNormType = 0
L2HysThreshold = 0.2
gammaCorrection = 1
nlevels = 64
signedGradients = True
hog = cv2.HOGDescriptor(winSize, blockSize, blockStride,
cellSize, nbins, derivAperture,
winSigma, histogramNormType, L2HysThreshold,
gammaCorrection, nlevels, signedGradients)
#偏斜校正
def deskew(img):
SZ = 28
ret, thresh = cv2.threshold(img, 127, 255, 0)
contours, hierarchy = cv2.findContours(thresh, 1, 2)
cnt = contours[0]
m = cv2.moments(cnt)
if abs(m['mu02']) < 1e-2:
# no deskewing needed.
return img.copy()
# Calculate skew based on central momemts.
skew = m['mu11']/m['mu02']
# Calculate affine transform to correct skewness.
M = np.float32([[1, skew, -0.5 * SZ * skew], [0, 1, 0]])
# Apply affine transform
img = cv2.warpAffine(img, M, (SZ, SZ), flags=cv2.WARP_INVERSE_MAP | cv2.INTER_LINEAR)
return img
def data(path):
images = []
lables = []
indexs = os.listdir(path)
for index in indexs:
names = os.listdir(path + '\\' + index)
for name in names:
image_path = path + '\\' + index + '\\' + name
img = cv2.imread(image_path, 0)#灰度化
img_deskew = deskew(img)#偏斜校正
img_hsv = hog.compute(img_deskew)
images.append(np.squeeze(img_hsv))
lables.append(int(index))
return np.array(images), np.array(lables)
train_data, train_lable = data('digit_data\\train')
print(train_data.shape)
images_test, lables_test = data('digit_data\\test')
print(images_test.shape)
clf = make_pipeline(StandardScaler(), SVC(gamma='auto'))
clf.fit(train_data, train_lable)
result = clf.predict(images_test)
correct = np.sum(result == lables_test)
print('SVM分类准确率: ', correct/len(images_test))
neigh = KNeighborsClassifier(n_neighbors=3)
neigh.fit(train_data, train_lable)
result = neigh.predict(images_test)
correct = np.sum(result == lables_test)
print('KNN分类准确率: ', correct/len(images_test))
3.使用 CNN 模型实现数字图像识别
from tensorflow import keras
from keras.models import Sequential
from keras.layers import Dense, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import optimizers
import os
import cv2
import numpy as np
def data(path):
images = []
lables = []
indexs = os.listdir(path)
for index in indexs:
names = os.listdir(path + '\\' + index)
for name in names:
image_path = path + '\\' + index + '\\' + name
img = cv2.imread(image_path, 0)
images.append(np.array(img))
lables.append(index)
return np.array(images), np.array(lables)
if __name__ == "__main__":
x_train, y_train = data('digit_data\\train')
x_test, y_test = data('digit_data\\test')
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train = x_train / 255.0
x_test = x_test / 255.0
x_train = x_train.reshape(x_train.shape[0], 28, 28, 1)
y_train = keras.utils.to_categorical(y_train, 10)
x_test = x_test.reshape(x_test.shape[0], 28, 28, 1)
y_test = keras.utils.to_categorical(y_test, 10)
print (x_train.shape)
print (y_train.shape)
#build the model
model = Sequential()
model.add(Conv2D(32,(5,5),activation = 'relu',input_shape = (28,28,1),padding='same'))
model.add(MaxPooling2D(pool_size = (2,2)))
model.add(Conv2D(64,(5,5),activation = 'relu',padding='same'))
model.add(MaxPooling2D(pool_size = (2,2)))
model.add(Flatten())
model.add(Dense(1024,activation = 'relu'))
model.add(Dense(10,activation = 'softmax'))
sgd = optimizers.SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True)
model.compile(loss=keras.losses.categorical_crossentropy,optimizer=sgd,metrics=['accuracy'])
model.fit(x_train, y_train, batch_size = 100, epochs = 14)
# save architecture
model.save_weights('CNN_model')
#load
#model.load_weights('cnn_model')
score = model.evaluate(x_test, y_test)
print ("loss: "+str(score[0]))
print ("accuracy: "+str(score[1]))