vector 二维数组_Leetcode刷题——数组与矩阵1
我的Leetcode刷题参考题目指北:
1. 牛客网:leetcode专题(为leetcode的前148道题)
2. leetcode的《初级算法》题集
3.leetcode的《高频面试题汇总》题集
4. github上目前见过最好的高频题整理:
https://github.com/CyC2018/CS-Notes/blob/master/notes/Leetcode%20%E9%A2%98%E8%A7%A3%20-%20%E7%9B%AE%E5%BD%95.md
计划是按照类型来刷,以刷简单题+中等题为主,hard目前不刷。
刷题流程:
至多5分钟思考思路 + 如果有思路尝试自己写代码;如果实在没思路直接看题解,看完之后自己敲代码写一遍;重点在于梳理和复习,我个人而言,手写是最有效的记忆方式。所以会在每次刷那么45678道题结束后,整理思路、重写代码。
数据结构相关
链表
树
栈和队列
哈希表
字符串
数组与矩阵
图
位运算
算法思想
双指针
排序
贪心思想
二分查找
分治
搜索
动态规划
数学
所以,从数组与矩阵开始。
今天的7道题选自牛客网,都是数组的简单题。
往下翻有全部的题目描述和对应代码,但实际上更重要的应该是手写的整理和记忆。
具体题目和对应代码:
LC138
给定n个非负整数a1,a2,…,an,其中每个数字表示坐标(i, ai)处的一个点。以(i,ai)和(i,0)(i=1,2,3...n)为端点画出n条直线。你可以从中选择两条线与x轴一起构成一个容器,最大的容器能装多少水?
注意:你不能倾斜容器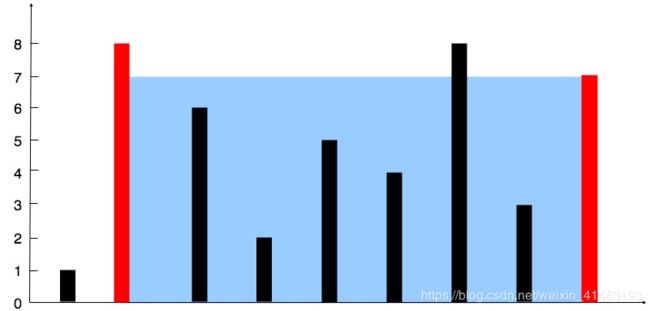
例如:
输入 [1,8,6,2,5,4,8,3,7]
输出: 49
class Solution {
public: /** * * @param height int整型vector * @return int整型 */ int maxArea(vector& height) {
// write code here int l=0; int r = height.size()-1; int Max = 0; while(l Max = max(Max, (r-l) * min(height[l], height[r])); height[l] } return Max; }}; LC123
给定一个数组和一个值,使用就地算法将数组中所有等于这个值的元素删除,并返回新数组的长度。
元素的顺序可以更改。你不用去关心大于当前数组长度的空间里面存储的值
class Solution {
public: int removeElement(int A[], int n, int elem) {
int j = 0; for (int i = 0; i < n; i++){
if (A[i] != elem){
A[j] = A[i]; j++; } } return j; }};LC102
给出一个用二维矩阵表示的图像
返回该图像顺时针旋转90度的结果
扩展:
你能使用原地算法解决这个问题么?
class Solution {
public: void rotate(vector > &matrix) {
//原地算法,所以不可以新建一个matrix int n = matrix.size(); //先以y=x为轴作对称 for (int i = 0; i < n; i ++){
for (int j = 0; j < matrix[i].size()-i; j++){
swap(matrix[i][j], matrix[n-1-j][n-1-i]); } } //然后以x轴作对称 for (int k = 0; k < n/2 ; k++){
for (int m = 0; m < matrix[k].size(); m++){
swap(matrix[k][m], matrix[n-1-k][m]); } } }}; LC91
给定一个整数n,将数字1到nn^22按螺旋的顺序填入n×n的矩阵
例如:
给出的n=3,
你应该返回如下矩阵:
[↵ [ 1, 2, 3 ],↵ [ 8, 9, 4 ],↵ [ 7, 6, 5 ]↵]class Solution {
public: /** * * @param n int整型 * @return int整型vector> */ vector > generateMatrix(int n) {
// write code here vector > matrix(n,vector(n)); int count = 1; while (count <= n*n){
for (int i = 0; i for (int j = i; j matrix[i][j] = count; count++; } for (int k = i+1; k matrix[k][n-1-i] = count; count++; } for (int m = n-2-i; m>=i; m--){
matrix[n-i-1][m] = count; count++; } for (int l = n-2-i; l>i; l--){
matrix[l][i] = count; count++; } } } return matrix; }}; LC74 荷兰国旗问题
现在有一个包含n个物体的数组,其中物体颜色为颜色为红色、白色或蓝色,请对这个数组进行排序,让相同颜色的物体相邻,颜色的顺序为红色,白色,蓝色。
我们用0,1,2分别代表颜色红,白,蓝
注意:
本题要求你不能使用排序库函数
扩展:
一个非常直接的解法是两步的计数排序的算法
首先:遍历一遍数组,记录0,1,2的数量,然后重写这个数组,先将0写入,再将1写入,再将2写入
你能给出一个只用一步,并且能在常数级空间复杂度解决这个问题的算法吗?
class Solution {
public: void sortColors(int A[], int n) {
int zero = 0; int two = n-1; for (int i = 0; i while (A[i]==2 && i < two) swap(A[i], A[two--]); while (A[i]==0 && i > zero) swap(A[i], A[zero++]); } }};LC30、29
假设你有一个数组,其中第i个元素是某只股票在第i天的价格。
如果你最多只能完成一笔交易(即买一股和卖一股股票),设计一个算法来求最大利润。
class Solution {
public: /** * * @param prices int整型vector * @return int整型 */ int maxProfit(vector& prices) {
// write code here int min = prices[0]; int profit = 0; for (int i = 0; i < prices.size(); i++){
if (prices[i] < min) min = prices[i]; profit = max(profit, prices[i]-min); } return profit; }}; 假设你有一个数组,其中第i个元素表示某只股票在第i天的价格。
设计一个算法来寻找最大的利润。你可以完成任意数量的交易(例如,多次购买和出售股票的一股)。但是,你不能同时进行多个交易(即,你必须在再次购买之前卖出之前买的股票)。
class Solution {
public: /** * * @param prices int整型vector * @return int整型 */ int maxProfit(vector& prices) {
// write code here //分析可知,要想利益最大化,就应该每次在波谷买进,波峰卖出,这样利益最大,操作次数最少 //应该是使用动态规划来做可能比较简洁。 int profit = 0; int n = prices.size(); int changes[n]; for (int i = 1; i < n; i++){
changes[i-1] = prices[i] - prices[i-1]; if (changes[i-1] > 0) profit += changes[i-1]; } return profit; }}; 





