写在前面:
对Metal技术感兴趣的同学,可以关注我的专题:Metal专辑
也可以关注我个人的账号:张芳涛
所有的代码存储的Github地址是:Metal
正文
让我们继续使用Metal着色语言(MSL)继续我们的着色世界之旅,在第11部分中选择我们离开的地方。使用我们上次工作的同一个Playground,接下来我们将尝试接近使用Metal着色语言 MSL数学函数,如sin,cos,pow,abs,fmod,clamp,mix,step和smoothstep。
首先,让我们看看上次的“日食”代码。 奇怪的是,我们从上面的函数列表的末尾开始,因为smoothstep是我们需要解决上次问题所需的函数而我们没有注意它 - 我们的输出图像有锯齿,你可以看到 如果我们放大到足以让它可见:
smoothstep函数取决于左边缘小于右边缘。 该函数将实数x作为输入,如果x小于或等于左边缘则输出0,如果x大于或等于右边缘则输出1,否则平滑插值在0和1之间。 step和smoothstep函数之间的区别在于step在边缘处突然从0跳到1。 smoothstep函数在执行钳位后实现三次Hermite插值。 名为smootherstep的改进版本在x = 0和x = 1时具有零一阶和二阶导数:
smoothstep(X) = 3X^2 - 2X^3
smootherstep(X) = 6X^5 - 15X^4 + 10X^3
让我们实现smootherstep()函数:
float smootherstep(float e1, float e2, float x)
{
x = clamp((x - e1) / (e2 - e1), 0.0, 1.0);
return x * x * x * (x * (x * 6 - 15) + 10);
}
给定最小值和最大值时,clamp()函数将点移动到最接近的可用值。 如果小于它,则输入采用min的值,如果大于它,则输入max的值,并且如果介于两者之间则保持其值。 我们的计算内核现在应该如下所示:
int width = output.get_width();
int height = output.get_height();
float2 uv = float2(gid) / float2(width, height);
uv = uv * 2.0 - 1.0;
float distance = distToCircle(uv, float2(0), 0.5);
float xMax = width/height;
float4 sun = float4(1, 0.7, 0, 1) * (1 - distance);
float4 planet = float4(0);
float radius = 0.5;
float m = smootherstep(radius - 0.005, radius + 0.005, length(uv - float2(xMax-1, 0)));
float4 pixel = mix(planet, sun, m);
output.write(pixel, gid);
我们在继续之前看到的最后一个功能是混合。 mix()函数使用它们之间的权重来执行x和y之间的线性插值。 返回值计算为x *(1-w)+ y * w。 在这种情况下,使用平滑步骤作为权重来插值行星颜色和太阳颜色。 如果您执行playground,输出图像现在具有抗锯齿功能,并且锯齿状全部消失:
我们看到的下一个功能是abs和fmod。 abs()函数只返回绝对值,或者数字的距离为0.换句话说,任何值都会丢失其符号并始终返回非负值。fmod()函数返回float的余数小数部分(相当于整数的模运算符%)。 让我们将这两个函数应用于某些值,看看我们能得到什么:
float3 color = float3(0.7);
if(fmod(uv.x, 0.1) < 0.005 || fmod(uv.y, 0.1) < 0.005) color = float3(0,0,1);
float2 uv_ext = uv * 2.0 - 1.0;
if(abs(uv_ext.x) < 0.02 || abs(uv_ext.y) < 0.02) color = float3(1, 0, 0);
if(abs(uv_ext.x - uv_ext.y) < 0.02 || abs(uv_ext.x + uv_ext.y) < 0.02) color = float3(0, 1, 0);
output.write(float4(color, 1), gid);
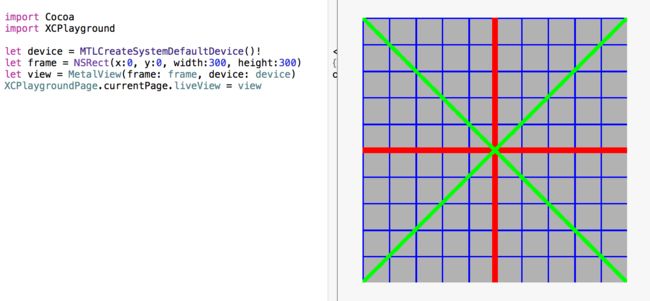
输出图像应如下所示:
首先,我们绘制了一条蓝色线条,它们之间的间距为0.1,宽度为0.005。 接下来,我们对屏幕坐标进行标准化,以便我们可以使用[-1,1]间隔,然后将X和Y轴绘制成红色,宽度为0.02。 最后,我们将两个对角线绘制成绿色,宽度相同,记住x - y给出了减小的斜率(对角线),而x + y给出了增加的斜率。
最后,让我们使用sin(),cos(),fract(),dot()和pow()以及我们已经讨论过的其他函数:
float2 cc = 1.1 * float2(0.5 * cos(0.1) - 0.25 * cos(0.2), 0.5 * sin(0.1) - 0.25 * sin(0.2) );
float4 dmin = float4(1000.0);
float2 z = (-1.0 + 2.0*uv) * float2(1.7, 1.0);
for(int i=0; i<64; i++) {
z = cc + float2(z.x * z.x - z.y * z.y, 2.0 * z.x * z.y);
dmin=min(dmin, float4(abs(0.0 + z.y + 0.5 * sin(z.x)), abs(1.0 + z.x + 0.5 * sin(z.y)), dot(z, z), length(fract(z) - 0.5)));
}
float3 color = float3(dmin.w);
color = mix(color, float3(1.00, 0.80, 0.60), min(1.0, pow(dmin.x * 0.25, 0.20)));
color = mix(color, float3(0.72, 0.70, 0.60), min(1.0, pow(dmin.y * 0.50, 0.50)));
color = mix(color, float3(1.00, 1.00, 1.00), 1.0 - min(1.0, pow(dmin.z * 1.00, 0.15)));
color = 1.25 * color * color;
color *= 0.5 + 0.5 * pow(16.0 * uv.x * (1.0 - uv.x) * uv.y * (1.0 - uv.y), 0.15);
output.write(float4(color, 1), gid);
sin()函数只是一个角度的正弦,cos()函数显然是一个角度的余弦,fract()函数返回一个值的小数部分,dot()函数返回两个标量乘积 向量,最后,pow()函数返回一个数字的值,增加到另一个数字的幂。 这段代码产生了一个美丽的分形,一个真正的艺术作品由Inigo Quilez提供。 输出图像应如下所示:
源代码在这里