堆排序与海量TopK问题
系列文章目录
文章目录
- 系列文章目录
- 前言
- 一、堆排序
-
-
- 1.什么是堆
-
- 二、堆排序原理
-
-
- 1.堆排序的实现
-
- 三、海量TopK问题
-
-
- 1.第一种解法
- 2.第二种解法
-
- 总结
前言
排序算法是个老生常谈的问题,笔试要考,面试也问,不过翻来覆去也就那几个花样吧。大概理解一下各个算法的原理,记下表格里的数据,然后再试试手撕代码,基本上就没问题了。
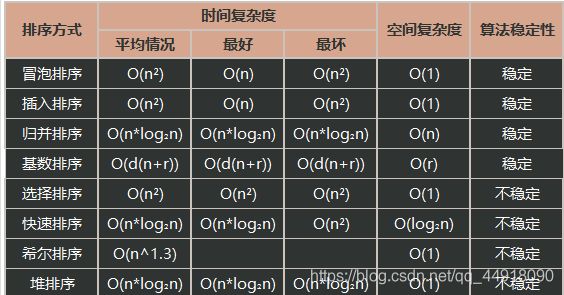
从表格里可以看出,堆排序是一个时间和空间复杂度都比较优秀的算法,至于它的原理,看懂是肯定能轻易看懂的,但是我总觉得如果你不自己亲手写一遍,就很容易忘记。并且,用递归的话,代码也是很简短的。
一、堆排序
1.什么是堆

堆(heap)是一种数据结构,也被称为优先队列(priority queue)。队列中允许的操作是先进先出(FIFO),在队尾插入元素,在队头取出元素。而堆也是一样,在堆底插入元素,在堆顶取出元素,但是堆中元素的排列不是按照到来的先后顺序,而是按照一定的优先顺序排列的。这个优先顺序可以是元素的大小或者其他规则。
而二叉堆是一种特殊的堆,它是完全二元树(二叉树)或者是近似完全二元树(二叉树)。二叉堆有两种:最大堆和最小堆。最大堆:父结点的键值总是大于或等于任何一个子节点的键值;最小堆:父结点的键值总是小于或等于任何一个子节点的键值。如下图。
二、堆排序原理
堆排序(HeapSort)是指利用堆这种数据结构所设计的一种排序算法。它的关键在于建堆和调整堆。步骤主要如下:
- 创建一个堆;
- 把堆首(最大值)和堆尾互换;
- 把堆的尺寸缩小1,并调整堆,把新的数组顶端数据调整到相应位置;
- 重复步骤 2,直到堆的尺寸为1,此时排序结束。
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。

当然,光看文字肯定不能很直观地理解,我们跟着图示来学习吧。现在,我们有一个待排序的数组 {2, 4, 3, 7, 5, 8},我们通过构建最大堆的方法来排序。
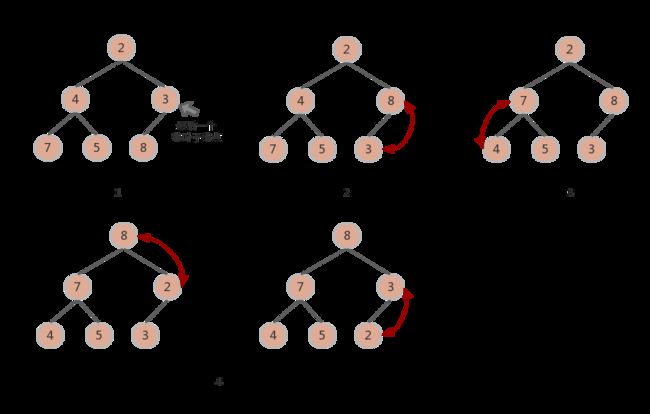
对于建堆时间复杂度是O(N):

1.堆排序的实现
代码如下:
void swap(int* left, int* right)
{
int tmp = 0;
tmp = *left;
*left = *right;
*right = tmp;
}
void AdjustDown(int* arr, int sz, int parent)
{
int child = 2 * parent + 1;
while (child < sz)
{
if (child + 1 < sz&&arr[child + 1] > arr[child])
{
child++;
}
if (arr[child]>arr[parent])
{
swap(&arr[child], &arr[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
//排升序,建大堆
void HeapSort(int *arr, int sz)
{
//建堆
int i = (sz - 1 - 1) / 2;
for (i = (sz - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, sz, i);
}
int end = sz - 1;
while (end > 0)
{
//选出次大的
swap(&arr[0], &arr[end]);
//最后一个不用交换,所以为n-1个数为end
AdjustDown(arr, end, 0);
end--;
}
}
三、海量TopK问题
最小的K个数
指Offer有这样一道题,求最小的K个数,题目描述:输入n个整数,找出其中最小的K个数。例如输入 4,5,1,6,2,7,3,8 这8个数字,则最小的4个数字是 1,2,3,4。
而在面试的时候,我们也可能遇到这样的问题:有一亿个浮点数,如何找出其中最大的10000个?
这类问题我们把称为TopK问题:指从大量数据(源数据)中获取最大(或最小)的K个数据。

1.第一种解法
建立一个大小为arrSize的堆,用进堆和出堆HeapPop和HeapTop两种方法,
代码如下:
void HeapInit(struct Heap* hp, HPDataType* a, int n) //初始化堆
{
assert(hp);
hp->a = (HPDataType*)malloc(sizeof(HPDataType)*n);
if (hp->a == NULL)
{
printf("malloc fail!\n");
exit(-1);
}
memcpy(hp->a, a, sizeof(HPDataType)*n);
hp->size = n;
hp->capacity = n;
int i = 0;
for (i = (hp->size - 2) / 2; i >= 0; i--)
{
AdjustDown(hp->a, hp->size, i);
}
}
void HeapPop(struct Heap* hp)
{
assert(hp);
assert(hp->size > 0);
Swap(&hp->a[0], &hp->a[hp->size - 1]);
hp->size--; //删除掉堆底数据
AdjustDown(hp->a, hp->size, 0);
}
HPDataType HeapTop(struct Heap* hp)
{
assert(hp);
assert(hp->size != 0);
return hp->a[0];
}
int* getLeastNumbers(int* arr, int arrSize, int k, int* returnSize)
{
struct Heap hp;
HeapInit(&hp, arr, arrSize);
int* ret = (int*)malloc(sizeof(int)*k);
for (int i = 0; i<k; i++)
{
ret[i] = HeapTop(&hp);
HeapPop(&hp);
}
*returnSize = k;
return ret;
}
2.第二种解法
我们可以先取下标 0~k-1 的局部数组,用它来维护一个大小为K的数组,然后遍历后续的数字,进行比较后决定是否替换。这时候堆排序就派上用场了。我们可以将前K个数字建立为一个最大堆,如果是要取最大的K个数,则在后续遍历中,将数字与最大堆的堆顶数字进行比较,若比它小,则进行替换,然后再重新调整为最大堆。整个过程直至所有数字遍历完为止。时间复杂度为O(n*log₂K),空间复杂度为K。
代码如下:
#define _CRT_SECURE_NO_WARNINGS 1
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
#include关键:
相似的TopK问题还有:
- 有10000000个记录,这些查询串的重复度比较高,如果除去重复后,不超过3000000个。一个查询串的重复度越高,说明查询它的用户越多,也就是越热门。请统计最热门的10个查询串,要求使用的内存不能超过1GB。
- 有10个文件,每个文件1GB,每个文件的每一行存放的都是用户的query,每个文件的query都可能重复。按照query的频度排序。
- 有一个1GB大小的文件,里面的每一行是一个词,词的大小不超过16个字节,内存限制大小是1MB。返回频数最高的100个词。
- 提取某日访问网站次数最多的那个IP。
- 10亿个整数找出重复次数最多的100个整数。
- 搜索的输入信息是一个字符串,统计300万条输入信息中最热门的前10条,每次输入的一个字符串为不超过255B,内存使用只有1GB。
- 有1000万个身份证号以及他们对应的数据,身份证号可能重复,找出出现次数最多的身份证号。
等等…
总结
以上就是今天要讲的内容,本文仅仅简单介绍了堆中堆排序和热门问题TopK的解法,而堆提供了大量能使我们快速便捷地处理数据的函数和方法,我们务必掌握。另外,如果有需要源码的私信我即可。还有,如果上述有任何问题,请懂哥指教,不过没关系,主要是自己能坚持,更希望有一起学习的同学可以帮我指正,但是如果可以请温柔一点跟我讲,爱与和平是永远的主题,爱各位了。

