Leetcode_入门_二分查找
Leetcode_入门_二分查找
- 1、求开方
-
- 1）题目要求
- 2）我的解法
- 3）其他解法
- 4）自己的优化代码
- 5）学到的东西
- 2、大于给定元素的最小元素（744、Easy）
-
- 1）题目要求
- 2）我的解法
- 3）其他解法
- 4）自己的优化代码
- 5）学到的东西
- 3、有序数组中的单一元素（540、Medium）
-
- 1）题目要求
- 2）我的解法
- 3）其他解法
- 4）自己的优化代码
- 5）学到的东西
- 4、第一个错误的版本（278、Easy）
-
- 1）题目要求
- 2）我的解法
- 3）其他解法
- 4）自己的优化代码
- 5）学到的东西
- 5、旋转数组的最小数字（153、Medium）
-
- 1）题目要求
- 2）我的解法
- 3）其他解法
- 4）自己的优化代码
- 5）学到的东西
- 6、查找区间（34、Medium）
-
- 1）题目要求
- 2）我的解法
- 3）其他解法
- 4）自己的优化代码
- 5）学到的东西
- 总结
1、求开方
1）题目要求
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根，其中 x 是非负整数。
由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。
示例 1:
输入: 4
输出: 2
示例 2:
输入: 8
输出: 2
说明: 8 的平方根是 2.82842…,
由于返回类型是整数，小数部分将被舍去。
2）我的解法
c++
class Solution {
public:
int mySqrt(int x) {
long l=0,r=x;
long m=0;
while(l<=r)
{
m=(l+r)/2;
if(m*m==x||(m*m<x&&(m+1)*(m+1)>x))return m;
else if(m*m<x)l=m+1;
else r=m-1;
}
return m;
}
};
3）其他解法
方法一：袖珍计算器算法
class Solution {
public:
int mySqrt(int x) {
if (x == 0) {
return 0;
}
int ans = exp(0.5 * log(x));
return ((long long)(ans + 1) * (ans + 1) <= x ? ans + 1 : ans);
}
};
方法二：二分查找
class Solution {
public:
int mySqrt(int x) {
int l = 0, r = x, ans = -1;
while (l <= r) {
int mid = l + (r - l) / 2;
if ((long long)mid * mid <= x) {
ans = mid;
l = mid + 1;
}
else {
r = mid - 1;
}
}
return ans;
}
};
作者：LeetCode-Solution
链接：link
来源：力扣（LeetCode）
方法三：牛顿迭代
class Solution {
public:
int mySqrt(int x) {
if (x == 0) {
return 0;
}
double C = x, x0 = x;
while (true) {
double xi = 0.5 * (x0 + C / x0);
if (fabs(x0 - xi) < 1e-7) {
break;
}
x0 = xi;
}
return int(x0);
}
};
作者：LeetCode-Solution
链接：link
来源：力扣（LeetCode）
4）自己的优化代码
c++
class Solution {
public:
int mySqrt(int x) {
long l=0,r=x;
long m=0;
while(l<=r)
{
m=(l+r)/2;
if(m*m==x||(m*m<x&&(m+1)*(m+1)>x))return m;
else if(m*m<x)l=m+1;
else r=m-1;
}
return m;
}
};
5）学到的东西
牛顿迭代法
二分查找法
C++:fabs()为求浮点数的绝对值
abs()为求整数的绝对值
2、大于给定元素的最小元素（744、Easy）
1）题目要求
给你一个排序后的字符列表 letters ，列表中只包含小写英文字母。另给出一个目标字母 target，请你寻找在这一有序列表里比目标字母大的最小字母。
在比较时，字母是依序循环出现的。举个例子：
如果目标字母 target = ‘z’ 并且字符列表为 letters = [‘a’, ‘b’]，则答案返回 ‘a’
示例：
输入:
letters = [“c”, “f”, “j”]
target = “a”
输出: “c”
输入:
letters = [“c”, “f”, “j”]
target = “c”
输出: “f”
输入:
letters = [“c”, “f”, “j”]
target = “d”
输出: “f”
输入:
letters = [“c”, “f”, “j”]
target = “g”
输出: “j”
输入:
letters = [“c”, “f”, “j”]
target = “j”
输出: “c”
输入:
letters = [“c”, “f”, “j”]
target = “k”
输出: “c”
提示：
letters长度范围在[2, 10000]区间内。
letters 仅由小写字母组成，最少包含两个不同的字母。
目标字母target 是一个小写字母。
2）我的解法
c++
class Solution {
public:
char nextGreatestLetter(vector<char>& letters, char target) {
int l=0,r=letters.size()-1,mid=-1;
char result=' ';
while(l<=r)
{
mid=(l+r)/2;
if(letters[mid]>target){
result=letters[mid];r=mid-1;}
else l=mid+1;
}
if(result==' ')return letters[0];
else return result;
}
};
3）其他解法
方法一：记录存在的字母
算法：
我们可以扫描 letters 记录字母是否存在。我们可以用大小为 26 的数组或者 Set 来实现。
然后，从下一个字母（从比目标大一个的字母开始）开始检查一下是否存在。如果有的话则是答案。
class Solution {
public char nextGreatestLetter(char[] letters, char target) {
boolean[] seen = new boolean[26];
for (char c: letters)
seen[c - 'a'] = true;
while (true) {
target++;
if (target > 'z') target = 'a';
if (seen[target - 'a']) return target;
}
}
}
方法二：线性扫描
算法：
由于 letters 已经有序，当我们从左往右扫描找到比目标字母大字母则该字母就是答案。否则(letters 不为空)答案将是 letters[0]。
class Solution {
public char nextGreatestLetter(char[] letters, char target) {
for (char c: letters)
if (c > target) return c;
return letters[0];
}
}
方法三：二分查找
算法：
如方法二一样，我们想要在有序数组中查找比目标字母大的最小字母，可以使用二分查找：让我们找到最右边的位置将 target 插入 letters 中，以便它保持排序。
二分查找分几轮进行，在每一轮中我们保持循环始终在区间 [lo，hi]。让 mi = (lo + hi) / 2。若 letters[mi] <= target，则我们修改查找区间为 [mi + 1, hi]，否则，我们修改为 [lo, mi]
最后，如果插入位置是最后一个位置 letters.length，则返回 letters[0]。这就是模运算的运用。
class Solution {
public char nextGreatestLetter(char[] letters, char target) {
int lo = 0, hi = letters.length;
while (lo < hi) {
int mi = lo + (hi - lo) / 2;
if (letters[mi] <= target) lo = mi + 1;
else hi = mi;
}
return letters[lo % letters.length];
}
}
作者：LeetCode
链接：link
来源：力扣（LeetCode）
4）自己的优化代码
c++
class Solution {
public:
char nextGreatestLetter(vector<char>& letters, char target) {
int l=0,r=letters.size()-1,mid=-1;
char result=' ';
while(l<=r)
{
mid=(l+r)/2;
if(letters[mid]>target){
result=letters[mid];r=mid-1;}
else l=mid+1;
}
if(result==' ')return letters[0];
else return result;
}
};
5）学到的东西
二分查找法
3、有序数组中的单一元素（540、Medium）
1）题目要求
给定一个只包含整数的有序数组，每个元素都会出现两次，唯有一个数只会出现一次，找出这个数。
示例 1:
输入: [1,1,2,3,3,4,4,8,8]
输出: 2
示例 2:
输入: [3,3,7,7,10,11,11]
输出: 10
注意: 您的方案应该在 O(log n)时间复杂度和 O(1)空间复杂度中运行
2）我的解法
c++
class Solution {
public:
bool isfront(int mid,vector<int>& nums)
{
if(mid%2==0)
{
if(nums[mid]==nums[mid-1])return true;
else return false;
}
else
{
if(nums[mid]==nums[mid-1])return false;
else return true;
}
}
int singleNonDuplicate(vector<int>& nums) {
int l=0,r=nums.size()-1,mid=-1;
if(nums.size()==1)return nums[0];
while(l<=r)
{
mid=(l+r)/2;
if(mid==0&&nums[mid]!=nums[mid+1])break;
else if(mid==nums.size()-1&&nums[mid]!=nums[mid-1])break;
else if(nums[mid]!=nums[mid-1]&&nums[mid]!=nums[mid+1])break;
else if(isfront(mid,nums))r=mid-1;
else l=mid+1;
}
return nums[mid];
}
};
3）其他解法
（1）
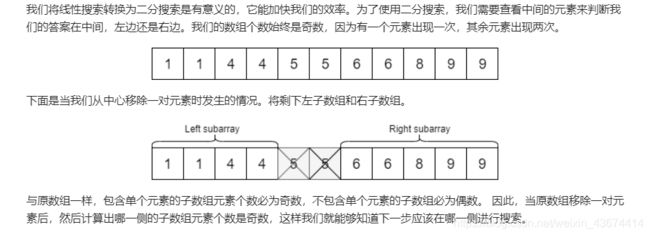我们首先将 lo 和 hi 指向数组首尾两个元素。然后进行二分搜索将数组搜索空间减半，直到找到单一元素或者仅剩一个元素为止。当搜索空间只剩一个元素，则该元素就是单个元素。
在每个循环迭代中，我们确定 mid，变量 halvesAreEven = (hi - mid) % 2 == 0。 通过查看中间元素同一元素为哪一个（左侧子数组中的最后一个元素或右侧子数组中的第一个元素），我们可以通过变量 halvesAreEven 确定现在哪一侧元素个数为奇数，并更新 lo 和 hi。
最难的部分是根据 mid 和 halvesAreEven 的值正确更新 lo 和 hi。我们通过下图来帮助我们理解
class Solution {
public:
int singleNonDuplicate(vector<int>& nums) {
int lo = 0;
int hi = nums.size() - 1;
while (lo < hi) {
int mid = lo + (hi - lo) / 2;
bool halvesAreEven = (hi - mid) % 2 == 0;
if (nums[mid + 1] == nums[mid]) {
if (halvesAreEven) {
lo = mid + 2;
} else {
hi = mid - 1;
}
} else if (nums[mid - 1] == nums[mid]) {
if (halvesAreEven) {
hi = mid - 2;
} else {
lo = mid + 1;
}
} else {
return nums[mid];
}
}
return nums[lo];
}
};
（2）仅对偶数索引进行二分搜索
事实证明我们只需要对偶数索引进行二分搜索。这种方法与方法二都是不错的方法，但是该方法比方法二更加优雅。
在该算法中，我们对所有偶数索引进行搜索，直到遇到第一个其后元素不相同的索引。
我们可以使用二分搜索替代线性搜索。
在单个元素的后面，则成对的元素变为奇数索引后跟他们的同一元素。说明我们在检索单个元素后面的偶数索引时，其后都没有它的同一元素。因此，我们可以通过偶数索引确定单个元素在左侧还是右侧。
算法：
奇数长度的数组首尾元素索引都为偶数，因此我们可以将 lo 和 hi 设置为数组首尾。
我们需要确保 mid 是偶数，如果为奇数，则将其减 1。
然后，我们检查 mid 的元素是否与其后面的索引相同。
如果相同，则我们知道 mid 不是单个元素。且单个元素在 mid 之后。则我们将 lo 设置为 mid + 2。
如果不是，则我们知道单个元素位于 mid，或者在 mid 之前。我们将 hi 设置为 mid。
一旦 lo == hi，则当前搜索空间为 1 个元素，那么该元素为单个元素，我们将返回它。
class Solution {
public:
int singleNonDuplicate(vector<int>& nums) {
int lo = 0;
int hi = nums.size() - 1;
while (lo < hi) {
int mid = lo + (hi - lo) / 2;
if (mid % 2 == 1) mid--;
if (nums[mid] == nums[mid + 1]) {
lo = mid + 2;
} else {
hi = mid;
}
}
return nums[lo];
}
};
作者：LeetCode
链接：link
来源：力扣（LeetCode）
4）自己的优化代码
c++
class Solution {
public:
bool isfront(int mid,vector<int>& nums)
{
if(mid%2==0)
{
if(nums[mid]==nums[mid-1])return true;
else return false;
}
else
{
if(nums[mid]==nums[mid-1])return false;
else return true;
}
}
int singleNonDuplicate(vector<int>& nums) {
int l=0,r=nums.size()-1,mid=-1;
if(nums.size()==1)return nums[0];
while(l<=r)
{
mid=(l+r)/2;
if(mid==0&&nums[mid]!=nums[mid+1])break;
else if(mid==nums.size()-1&&nums[mid]!=nums[mid-1])break;
else if(nums[mid]!=nums[mid-1]&&nums[mid]!=nums[mid+1])break;
else if(isfront(mid,nums))r=mid-1;
else l=mid+1;
}
return nums[mid];
}
};
5）学到的东西
二分查找法
仅对偶数进行二分搜索
判断两侧数字的个数为基数还是偶数
4、第一个错误的版本（278、Easy）
1）题目要求
你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, …, n]，你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
示例:
给定 n = 5，并且 version = 4 是第一个错误的版本。
调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true
所以，4 是第一个错误的版本。
2）我的解法
c++
双百
class Solution {
public:
int firstBadVersion(int n) {
int l=1,r=n,mid=-1;
while(l<=r)
{
mid=l+(r-l)/2;
if(isBadVersion(mid))
{
if(!isBadVersion(mid-1))break;
else r=mid-1;
}
else l=mid+1;
}
return mid;
}
};
3）其他解法
// The API isBadVersion is defined for you.
// bool isBadVersion(int version);
class Solution {
public:
int firstBadVersion(int n) {
int left = 1;
int right = n;
while (left < right) //相等时 即为第一个错误版本
{
int mid = left + (right - left) / 2;
if (!isBadVersion(mid)) //正确版本
{
left = mid + 1;
}
else //错误版本
{
right = mid;
}
}
return left;
}
};
作者：eric-345
链接：link
来源：力扣（LeetCode）
4）自己的优化代码
c++
class Solution {
public:
int firstBadVersion(int n) {
int l=1,r=n,mid=-1;
while(l<=r)
{
mid=l+(r-l)/2;
if(isBadVersion(mid))
{
if(!isBadVersion(mid-1))break;
else r=mid-1;
}
else l=mid+1;
}
return mid;
}
};
5）学到的东西
二分查找
5、旋转数组的最小数字（153、Medium）
1）题目要求
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
请找出其中最小的元素。
你可以假设数组中不存在重复元素。
示例 1:
输入: [3,4,5,1,2]
输出: 1
示例 2:
输入: [4,5,6,7,0,1,2]
输出: 0
2）我的解法
c++
class Solution {
public:
int findMin(vector<int>& nums) {
int l=0,r=nums.size()-1,mid=-1;
int result=nums[0];
while(l<=r)
{
mid=l+(r-l)/2;
if(nums[mid]<result)result=nums[mid];
else if(nums[mid]>=nums[0])l=mid+1;
else r=mid-1;
}
return result;
}
};
3）其他解法
class Solution {
public:
int findMin(vector<int>& nums) {
int left = 0;
int right = nums.size() - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] > nums[right]) {
left = mid + 1;
} else {
right = mid;
}
}
return nums[left];
}
};
题解较长，点进链接仔细看
作者：armeria-program
链接：link
来源：力扣（LeetCode）
4）自己的优化代码
c++
class Solution {
public:
int findMin(vector<int>& nums) {
int l=0,r=nums.size()-1,mid=-1;
while(l<r)
{
mid=l+(r-l)/2;
if(nums[mid]<nums[r])r=mid;
else l=mid+1;
}
return nums[l];
}
};
5）学到的东西
可以让mid和left,right进行比较
列举可能性找规律
6、查找区间（34、Medium）
1）题目要求
给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
你的算法时间复杂度必须是 O(log n) 级别。
如果数组中不存在目标值，返回 [-1, -1]。
示例 1:
输入: nums = [5,7,7,8,8,10], target = 8
输出: [3,4]
示例 2:
输入: nums = [5,7,7,8,8,10], target = 6
输出: [-1,-1]
2）我的解法
c++
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
vector<int> result(2,-1);
int l=0,r=nums.size()-1,mid=-1;
while(l<=r)
{
mid=l+(r-l)/2;
if(nums[mid]<target)l=mid+1;
else if(nums[mid]>target)r=mid-1;
else
{
l=mid;r=mid;
while(l!=0&&nums[l-1]==target)
{
l--;
}
result[0]=l;
while(r!=nums.size()-1&&nums[r+1]==target)
{
r++;
}
result[1]=r;
break;
}
}
return result;
}
};
3）其他解法
利用二分思想先找其左边界，再找其右边界即可，注意找左边界的时候，由右侧逼近；找右边界的时候，由左侧逼近，即可。
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
vector<int> res(2,-1);
if(nums.empty()) return res;
int n=nums.size(),l=0,r=n-1;
while(l<r){
int m=l+(r-l)/2;
if(nums[m]>=target) r=m;
else l=m+1;
}
if(nums[l]!=target) return res;
res[0]=l;
r=n;
while(l<r){
int m=l+(r-l)/2;
if(nums[m]<=target) l=m+1;
else r=m;
}
res[1]=l-1;
return res;
}
};
作者：唐炜依
来源：力扣（LeetCode）评论区第一条
4）自己的优化代码
c++
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
vector<int> result(2,-1);
int l=0,r=nums.size()-1,mid=-1;
if(nums.size()==0)return result;//特殊情况
while(l<r)
{
mid=l+(r-l)/2;
if(nums[mid]<target)l=mid+1;
else r=mid;
}
if(nums[l]!=target)return result;//特殊情况
result[0]=l;
r=nums.size();//记得重新初始化,不-1相当于在数组后面加了一个元素，方便处理
while(l<r)
{
mid=l+(r-l)/2;
if(nums[mid]>target)r=mid;
else l=mid+1;
}
result[1]=r-1;//记得-1
return result;
}
};
5）学到的东西
分别找左右边界，
学会二分查找的变种实现
public int binarySearch(int[] nums, int key) {
int l = 0, h = nums.length - 1;
while (l < h) {
int m = l + (h - l) / 2;
if (nums[m] >= key) {
h = m;
} else {
l = m + 1;
}
}
return l;
}
总结
正常实现
Input : [1,2,3,4,5]
key : 3
return the index : 2
public int binarySearch(int[] nums, int key) {
int l = 0, h = nums.length - 1;
while (l <= h) {
int m = l + (h - l) / 2;
if (nums[m] == key) {
return m;
} else if (nums[m] > key) {
h = m - 1;
} else {
l = m + 1;
}
}
return -1;
}
时间复杂度
二分查找也称为折半查找，每次都能将查找区间减半，这种折半特性的算法时间复杂度为 O(logN)。
m 计算
有两种计算中值 m 的方式：
m = (l + h) / 2
m = l + (h - l) / 2
l + h 可能出现加法溢出，也就是说加法的结果大于整型能够表示的范围。但是 l 和 h 都为正数，因此 h - l 不会出现加法溢出问题。所以，最好使用第二种计算法方法。
未成功查找的返回值
循环退出时如果仍然没有查找到 key，那么表示查找失败。可以有两种返回值：
-1：以一个错误码表示没有查找到 key
l：将 key 插入到 nums 中的正确位置
变种
二分查找可以有很多变种，实现变种要注意边界值的判断。例如在一个有重复元素的数组中查找 key 的最左位置的实现如下：
public int binarySearch(int[] nums, int key) {
int l = 0, h = nums.length - 1;
while (l < h) {
int m = l + (h - l) / 2;
if (nums[m] >= key) {
h = m;
} else {
l = m + 1;
}
}
return l;
}
该实现和正常实现有以下不同：
h 的赋值表达式为 h = m
循环条件为 l < h
最后返回 l 而不是 -1
在 nums[m] >= key 的情况下，可以推导出最左 key 位于 [l, m] 区间中，这是一个闭区间。h 的赋值表达式为 h = m，因为 m 位置也可能是解。