python - 作业6：函数拟合（附代码）

github指路 冲冲冲冲冲

----------------------------------原文–如下--------------------------------

首先夸一下自己上课没有睡着并且精神面貌极佳，美中不足的是我以为8.55上课所以迟到惹……

从后面开始讲，看到这个作业我都惊呆了，无法理解他的意思= =

截图为证，什么噪声啊拟合啊我感觉和老师上课讲的内容关联不是很大，或者说只有我听不懂系列，

先讲上课内容吧，这节课主要讲了三个库（算了还是等我先写完作业吧，头好大）
第一个库 叫

IPython

IPython是一个增强的python shell

这部分我迟到了 ，看了下同桌的笔记 ，提到了它可以让许多python对象的显示形式更友好；有更详细的异常显示；可以增强额外的命令；还有交互式的数据处理

然后对ipython进行了相应的功能介绍，包括：

Tab自动完成 + 内省 + 中断正在执行的代码 + 保留命令历史 + 找回忘记保存的变量 + 超级特殊的魔术命令

一个个来

Tab自动完成

Tab自动完成就是利用Tab键可以得到变量名和函数名或者说是显示模块调用或者你可能用到的常量等等等

内省

内省就是类似于对原始python help的改进，功能差别不大，增加和保留了一点点信息，删掉了类型的一些介绍

中断正在执行的代码

中断正在执行的代码，因为ipython是一个增强的shell ，但他还是一个shell，然后呢，是shell就得进行交互式数据处理，ok这里就会出现一种很想让人避免却很难避免的情况——命令行输错了，运行时间有点长，敲了回车之后不想运行代码了，怎么做呢，在ipython可以按下ctrl+c强制退出上一个命令，造福人类

保留命令历史

保留命令历史，和windows的cmd一样，按上箭头可以得到上一次操作，个人觉得也很实用

第五个

找回忘记的保存的变量

找回忘记的保存的变量。这个是默认的，不管你知道不知道ipython都会帮你做了（上面那个保留命令历史也是）老师给的说明是把最近的两个输出结果保存在名称为‘_’ 和 ‘__’的变量里。但是我有点不懂输出结果的话……计算结果保存与否系列，其实不是很懂，据说在运算时间较长的时候比较适用

魔术命令

高级兮兮的魔术命令，就是以%开头的指令，具体的话

上课讲到了一个计算代码运行时间的指令叫%timeit（代码块的话就%%timeit）

运行程序文件 %run（为了写的方便 一点 顺便讲了路径管理功能 也就是%bookmark 还有个改变路径的和cmd很像 %cd）

然后还讲了在交互模式下执行一段代码的命令 %cpaste（这里我没听太全面太明白太理解）……但是呢，老师在课上试了一下 ipython 可以之间复制一段代码在交互模式讲执行= =显然对应的python自带的dell不可以
还有%debug 是用来调试和定位异常的= =

ipython库到此结束

------------------------10/22更新------------------------

numpy库

numpy库通常用来进行高性能计算。前面不知道有没有讲到，python只考虑方便没考虑高效，换言之，两者也很难兼得- -，反正呢python的运行速度较于其他语言就像是在爬（比赛时间其他语言 1000ms，python 2000ms）

高效

提问：为什么numpy库比较高效呢

回答：他是建立在C/C++语言的基础上的，所以快呀!

也就是说访问这个库就相当于访问已经编译好的C/C++的库

调用

提问：要怎么调用呢

回答：import numpy (as np) (当然这是要在install这个库之后进行的操作)

?然后是numpy里面常见一个数据结构 ： 多维数组 array……

每个array都有两个属性，一个是shape（各维度大小）另一个是dtype（数据类型）

创建array

提问：怎么创建array呢

回答：np.array([list]) 这是最基础的方法，当然可以创建一些特殊的矩阵，比如eye方法，可以创建对角线型矩阵，arange方法可以创建一定范围内的一阶矩阵等等等

指定数据类型

提问：如何指定数据类型呢

回答：arr1=np.array([1,2,3],dtype=np.float64)

对数据进行索引和切片操作

提问：怎么对数据进行索引和切片操作呢

回答：索引和切片操作和原python序列是一样的（2维数组可索引两次），要注意的是索引和切片都部复制内容，需要使用.copy（）方法复制

不复制内容

提问：为什么不复制内容呢

回答：前面讲到numpy库是用来进行高性能运算的，所以说尽可能做到能不复制就复制。数据量巨大，会造成复制时间长、占用内存大的不便，也就是说这样不太好

np数组的元素运算

np数组的元素运算 ，就是一元运算 比如abs（）求绝对值，sqrt（）开根号这种类似的方法，

数组间运算

数组间运算，就是双目运算 比如 maxinum（）这种求两个数组里的最大数的方法（好像描述的不是很清楚……改天打个例子试试，理解中的话应该是[1,2,5],[2,3,4] 得到应该是[2,3,5]这个样子？？），

数组内容审核

数组内容审核，就是说对某些数组可能会有元素值缺失这种情况……[1,2,3]比如这样，如果不对其进行判断和处理的话，在程序运行时候就可能会产生一些难以找到的bug，所以就有了这个isnan（）的方法，方法返回一个bool 的数组，找出原数组种那些是NAN的位置.

数组重塑

数组重塑的方法 功能命名 reshape（），拿例子讲话，比如

a1=np.array([1.2.3.4.5.6])
a2=a1.reshape(2,3)
print(a2)

得到a2=[[1,2,3],[4,5,6]]

对数组增加内容

对数组增加内容: np.insert(arr1,p,arr2,axis=0)其中一个参数arr1是指带加入数据的数组，p指得是加入数据的起始位置，arr2是需要加入的数组，axis是指增加的维度值，二维的就是指行和列

矩阵运算

矩阵运算，比如arr.T()就是矩阵转置运算 np.dot(arr1,arr2)就是点乘运算

基本的一些功能

接下来就是基本的一些功能，比如max()找最大值 ，argmax()找最大值的位置

random模块

numpy库里的random模块 ， 比较特殊的是它可以生成符合某种分布的采样，比如说 normal正态分布/ binomial二项分布的采样等等

matrix

接下来！讲了numpy库里的另一个数据结构，也是存储多维数组的，就是matrix嗯。

matrix和array的三个主要区别

①matrix索引返回的是同阶矩阵，array返回的降阶的矩阵
举个栗子：
对于数据都是[[1,2,3],[4,5,6],[7,8,9]]的
a[0][0]返回的是1
m[0][0]返回的是[[1]]

②在matrix中，* 运算指的是矩阵乘法

③matrix有个属性I表示它的逆矩阵

然后np.asarray()可以讲matrix转换成array

建议

老师给的一个建议就是能使用numpy库里的操作就不要用python内置的循环和判断语句（原因无他，python在爬）

SciPy

第三个库就是SciPy，据说是用于数学、科学、工程领域的库，可以有效计算Numpy矩阵（这里老师没有过多介绍，可能希望我们能够自学成才吧，老师强调了很多遍学习的技巧，两遍叭？大概？？）

贴张图 表明心意 我希望我能行

---

10/23更新 拟合效果

然后就是作业了 那个拟合函数 其实我还是不太理解的样子
等我搞明白了就 ……

上课写的代码是利用 scipy库里的optimize模块里的 curve_fit子模块写的一个二次函数，xy的点都是随机的所以效果不是很好，
！！！！然后！！！！

我去截图的时候！！！看起来很不错呀！！！！

这个图，这是我看到的效果（目前为止）最好的一个

这是代码↓

import numpy as np
from scipy.optimize import leastsq
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
import random
xx = []
yy = []

def A(params, x):
    a, b, c = params
    return a * x ** 2 + b * x + c

def nosie():
    for i in range(0,10):
        x = random.uniform(1,10)
        y = random.uniform(2,30)
        xx.append(x)
        yy.append(y)

# ……

def error(params, x, y):
    return A(params, x) - y

def slovePara():
    p0 = [10, 10, 10]
    Para = leastsq(error, p0, args=(X, Y))
    return Para

Para = slovePara()
a, b, c = Para[0]

plt.figure(figsize=(8, 6))
plt.scatter(X, Y, color="green", label="sample data", linewidth=2)
x = np.linspace(0, 12, 100)y = a * x * x + b * x + c 
plt.plot(x, y, color="red", label="solution line", linewidth=2)
plt.legend()
plt.show()

然后，呢，我就想做一个效果好一点的拟合曲线

于是在w同学的帮助下

我得到了这样的效果图，用指数函数来拟合= =，利用 scipy库里的optimize模块里的 curve_fit子模块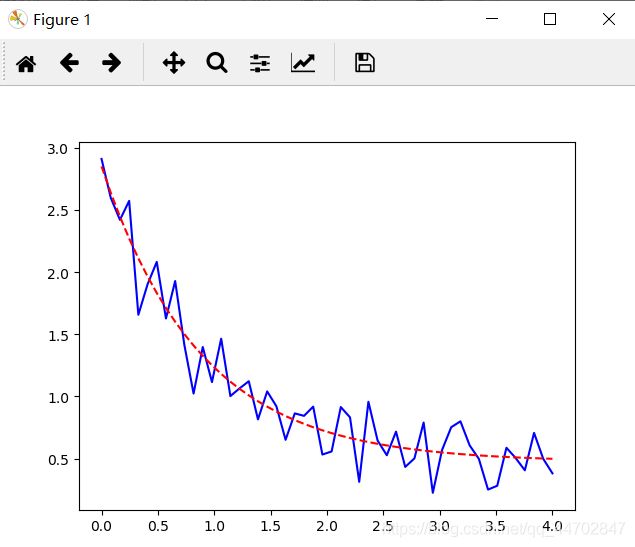

10月24日 完结更新

我对其进行了改进所以现在的代码大概长成这个样子：

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2019/10/22 10:37
# @Author : Chen Shan

import numpy as np
from scipy.optimize import leastsq
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
import random

# 1 ----------二次函数拟合，point （x，y）随机生成
xx = []
yy = []
def A(params, x):
    a, b, c = params
    return a * x ** 2 + b * x + c

def nosie():
    for i in range(0,10):
        x = random.uniform(1,10)
        y = random.uniform(2,30)
        xx.append(x)
        yy.append(y)

# ……
def error(params, x, y):
    return A(params, x) - y

def slovePara():
    p0 = [10, 10, 10]
    Para = leastsq(error, p0, args=(X, Y))
    return Para

Para = slovePara()
a, b, c = Para[0]
# print("a = "+ str(a) + ", b = "+ str(b) + ", c = "+ str(c))
# print("cost:" + str(Para[1]))
print("y = " + str(round(a, 2)) + "x*x+" + str(round(b, 2)) + "x+" + str(c))

plt.figure(figsize=(8, 6))
plt.scatter(X, Y, color="green", label="sample data", linewidth=2)

x = np.linspace(0, 12, 100)
y = a * x * x + b * x + c
plt.plot(x, y, color="red", label="solution line", linewidth=2)
plt.legend()
plt.show()

# # 2----------指数函数拟合，point x 随机生成
# def A2(x, a, b, c):
#     return a * np.exp(-b * x) + c
# # nosie
# xdata = np.linspace(0, 4, 50)
# y = A2(xdata, 2.5, 1.3, 0.5)
# ydata = y + 0.11 * np.random.normal(size=len(xdata))
#
# plt.plot(xdata, ydata, 'b-')
#
# popt, pcov = curve_fit(A2, xdata, ydata)
#
# y2 = [A2(i, popt[0], popt[1], popt[2]) for i in xdata]
# plt.plot(xdata, y2, 'r--')
#
# print("y = "+str(popt[0])+" * np.exp(-"+str(popt[1])+" * x) + "+str(popt[2]))
#
# plt.show()

2020/02/04更新code

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2019/10/22 10:37
# @Author : Chen Shan
# Function : Randomly generate 50 points, fit binary function and present

import numpy as np
from scipy.optimize import leastsq
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
import random

# 1 ----------二次函数拟合，point （x，y）随机生成
xx = []
yy = []
def A(params, x):
    a, b, c = params
    return a * x ** 2 + b * x + c

def nosie():
    for i in range(0,10):
        x = random.uniform(1,10)
        y = random.uniform(2,30)
        xx.append(x)
        yy.append(y)

nosie()
X = np.array(xx)
Y = np.array(yy)

# 误差函数，即拟合曲线所求的值与实际值的差
def error(params, x, y):
    return A(params, x) - y

# 对参数求解
def slovePara():
    p0 = [10, 10, 10]
    Para = leastsq(error, p0, args=(X, Y))
    return Para

Para = slovePara()
a, b, c = Para[0]
# print("a = "+ str(a) + ", b = "+ str(b) + ", c = "+ str(c))
# print("cost:" + str(Para[1]))
print("y = " + str(round(a, 2)) + "x*x+" + str(round(b, 2)) + "x+" + str(c))

plt.figure(figsize=(8, 6))
plt.scatter(X, Y, color="green", label="sample data", linewidth=2)

x = np.linspace(0, 12, 100)
y = a * x * x + b * x + c
plt.plot(x, y, color="red", label="solution line", linewidth=2)
plt.legend()
plt.show()

# # 2----------指数函数拟合，point x 随机生成
# def A2(x, a, b, c):
#     return a * np.exp(-b * x) + c
# # nosie
# xdata = np.linspace(0, 4, 50)
# y = A2(xdata, 2.5, 1.3, 0.5)
# ydata = y + 0.11 * np.random.normal(size=len(xdata))
#
# plt.plot(xdata, ydata, 'b-')
#
# popt, pcov = curve_fit(A2, xdata, ydata)
# # popt数组中，三个值分别是待求参数a,b,c
# y2 = [A2(i, popt[0], popt[1], popt[2]) for i in xdata]
# plt.plot(xdata, y2, 'r--')
#
# print("y = "+str(popt[0])+" * np.exp(-"+str(popt[1])+" * x) + "+str(popt[2]))
#
# plt.show()