POJ-1251 Jungle Roads

Jungle Roads

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 15610		Accepted: 6988

Description

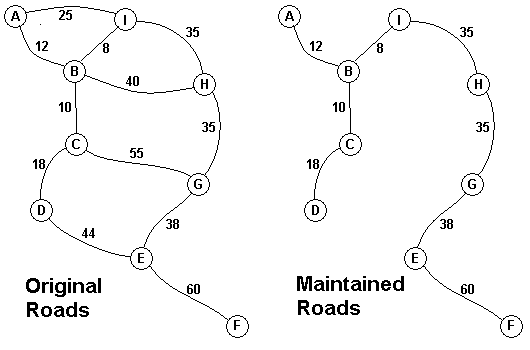
The Head Elder of the tropical island of Lagrishan has a problem. A burst of foreign aid money was spent on extra roads between villages some years ago. But the jungle overtakes roads relentlessly, so the large road network is too expensive to maintain. The Council of Elders must choose to stop maintaining some roads. The map above on the left shows all the roads in use now and the cost in aacms per month to maintain them. Of course there needs to be some way to get between all the villages on maintained roads, even if the route is not as short as before. The Chief Elder would like to tell the Council of Elders what would be the smallest amount they could spend in aacms per month to maintain roads that would connect all the villages. The villages are labeled A through I in the maps above. The map on the right shows the roads that could be maintained most cheaply, for 216 aacms per month. Your task is to write a program that will solve such problems.

Input

The input consists of one to 100 data sets, followed by a final line containing only 0. Each data set starts with a line containing only a number n, which is the number of villages, 1 < n < 27, and the villages are labeled with the first n letters of the alphabet, capitalized. Each data set is completed with n-1 lines that start with village labels in alphabetical order. There is no line for the last village. Each line for a village starts with the village label followed by a number, k, of roads from this village to villages with labels later in the alphabet. If k is greater than 0, the line continues with data for each of the k roads. The data for each road is the village label for the other end of the road followed by the monthly maintenance cost in aacms for the road. Maintenance costs will be positive integers less than 100. All data fields in the row are separated by single blanks. The road network will always allow travel between all the villages. The network will never have more than 75 roads. No village will have more than 15 roads going to other villages (before or after in the alphabet). In the sample input below, the first data set goes with the map above.

Output

The output is one integer per line for each data set: the minimum cost in aacms per month to maintain a road system that connect all the villages. Caution: A brute force solution that examines every possible set of roads will not finish within the one minute time limit.

Sample Input

9

A 2 B 12 I 25

B 3 C 10 H 40 I 8

C 2 D 18 G 55

D 1 E 44

E 2 F 60 G 38

F 0

G 1 H 35

H 1 I 35

3

A 2 B 10 C 40

B 1 C 20

0

Sample Output

216

30

  1 //代码一：普里母

  2 #include<stdio.h>

  3 #include<string.h>

  4 #define inf 0x3fffffff

  5 

  6 int map[30][30];

  7 

  8 int prim(int n)

  9 {

 10     int visit[30]={0};

 11     int dis[30];

 12     int sum,i,j,k,min;

 13     sum=0;

 14     for(i=0;i<n;++i)

 15         dis[i]=map[0][i];

 16     visit[0]=1;

 17     for(i=1;i<n;++i)

 18     {

 19         min=inf;

 20         k=0;

 21         for(j=0;j<n;++j)

 22         {

 23             if(!visit[j]&&min>dis[j])

 24             {

 25                 min=dis[j];

 26                 k=j;

 27             }

 28         }

 29         visit[k]=1;

 30         if(min!=inf)

 31             sum+=min;

 32         for(j=0;j<n;++j)

 33         {

 34             if(!visit[j]&&dis[j]>map[k][j])

 35                 dis[j]=map[k][j];

 36         }

 37     }

 38     return sum;

 39 }

 40 

 41 int main()

 42 {

 43     int n,len,k,i,j;

 44     char st[5],end[5];

 45     while(scanf("%d",&n),n)

 46     {

 47         for(i=0;i<n;++i)

 48             for(j=0;j<i;++j)

 49                 map[i][j]=map[j][i]=inf;

 50         for(i=1;i<n;++i)

 51         {

 52             scanf("%s%d",st,&k);

 53             while(k--)

 54             {

 55                 scanf("%s%d",end,&len);

 56                 if(len<map[st[0]-'A'][end[0]-'A'])

 57                 {

 58                     map[st[0]-'A'][end[0]-'A']=map[end[0]-'A'][st[0]-'A']=len;

 59                 }

 60             }

 61         }

 62         printf("%d\n",prim(n));

 63     }

 64     return 0;

 65 }

 66 

 67 //代码二：--克鲁斯卡尔

 68 

 69 /*

 70  Kruskal算法的基本思想

 71  假设WN=(V,{E})是一个含有n个顶点的连通网，则按照克鲁斯卡尔算法构造最小生成树的过程为：

 72  先构造一个只含n个顶点，而边集为空的子图，

 73  若将该子图中各个顶点看成是各棵树上的根结点，则它是一个含有n棵树的一个森林。

 74  之后，从网的边集E中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，

 75  也就是说，将这两个顶点分别所在的两棵树合成一棵树；

 76  反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。

 77  依次类推，直至森林中只有一棵树，也即子图中含有n-1条边为止。

 78  */

 79  #include<iostream>

 80  #include<cstdlib>

 81  #include<cstdio>

 82  #include<cstring>

 83  #include<algorithm>

 84  #include<cmath>

 85  using namespace std;

 86  const int inf = ( 1 << 20 ) ;

 87  int p[27];        //    并查集，用于判断两点是否直接或间接连通

 88  struct prog {

 89      int u;

 90      int v;

 91      int w;

 92  }map[80];//存储边的信息，包括起点/终点/权值

 93  bool cmp ( prog a , prog b)

 94  {//排序函数，将边根据权值从小到大排

 95      return a.w<b.w;

 96  }

 97  int find(int x)

 98  {//并查集的find，不解释

 99      return x==p[x]?x:p[x]=find(p[x]);

100  }

101  int main()

102  {

103      int n;

104      while ( cin >> n , n ) 

105      {

106          int i , j ;

107          for  ( i = 0 ; i < 27  ; i ++ )

108              p[i] = i ;//并查集初始化

109          int k = 0 ;

110          for ( i = 0 ; i < n - 1 ; i ++ )

111          {//构造边的信息

112              char str[3];

113              int m;

114              cin >> str >> m ;

115              for ( j = 0 ; j < m ; j ++ ,k ++ )

116              {

117                  char str2[3];

118                  int t;

119                  cin >> str2 >> t ;

120                  map[k].u=(str[0]-'A');

121                  map[k].v=(str2[0]-'A');

122                  map[k].w=t;

123              }

124          }

125  

126          sort ( map , map + k , cmp );//将边从小到大排序

127          int ans=0;        //所要求的答案

128          for ( i = 0 ; i < k ; i ++ )

129          {

130              int x = find(map[i].u);

131              int y = find(map[i].v);

132              if( x!=y)

133              {//如果两点不在同一连通分量里，则将两点连接，并存储该边

134                  ans+=map[i].w;

135                  p[x]=y;

136              }

137          }

138          cout<<ans<<endl;

139      }

140      return 0;

141  }