【C语言基础学习笔记】五、操作符详解（1）（详细讲解+代码举例+练习巩固）

有些人是因为看见而相信，有些人则是因为相信而看见。相信自己，成为自己生命的那道光，才能照亮前方黑暗的道路，看见希望的曙光。

---

---

一、算术操作符

+ - * / %

1.除了 % 操作符之外，其他的几个操作符可以作用于整数和浮点数
2.对于 / 操作符如果两个操作数都为整数，执行整数除法（求商舍余）。而只要有浮点数，执行的就是浮点数除法。
3. % 操作符的两个操作数必须为整数，若其中一个不为整数则报错，返回的是整除之后的余数。

#include
int main()
{
     
	int a = 5;
	int b = 2;
	int c = 0;
	printf("a+b = %d\n", a + b);//相加
	printf("a-b = %d\n", a - b);//相减
	printf("a*b = %d\n", a * b);//相乘
	printf("a/b = %d\n", a / b);//求商
	printf("a%%b = %d\n", a % b);//取模
	return 0;
}

#include
int main()
{
     
	/*double a = 5.0 / 2;*/
	double a = 5 % 2.0;//报错
	printf("a = %lf", a);
	return 0;
}

---

二、移位操作符

<< >>

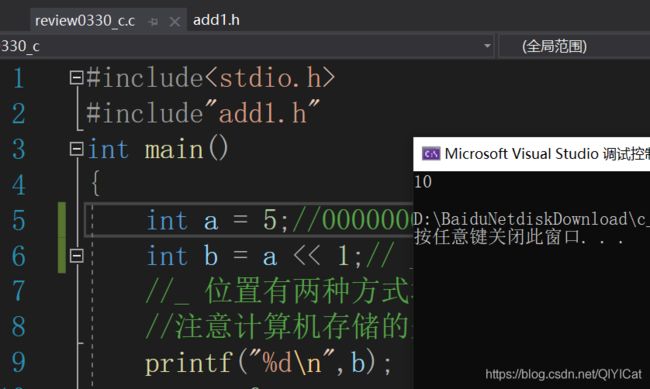
左移操作符 << 操作二进制补码
移位规则：左边抛弃、右边补0

总结：左移移动一位正数相当于直接乘以2，负数也一样，移动n位，乘以2 ^ n。

右移操作符 << 操作的是二进制补码

计算机中的数字都是以补码的形式存储的，其中正数原码、反码、补码相同，负数的反码由原码按位取反（符号位不变）求得，补码 = 反码 + 1。
十进制：1 二进制原码 / 反码 / 补码:00000000 00000000 00000000 00000001
十进制： - 1
二进制原码：10000000 00000000 00000000 00000001
二进制反码：11111111 11111111 11111111 11111110
二进制补码：11111111 11111111 11111111 11111111

-1 >> 1（右移一位） 二进制补码：_1111111 11111111 11111111 11111111
首先右移运算分两种 :
1.算术移位左边用原该值的符号位填充，右边丢弃
2.逻辑移位左边用0填充，右边丢弃

按照算术移位 那么_该填充 1 二进制补码：11111111 11111111 11111111 11111111 -> - 1(转原码）
按照逻辑移位 那么_该填充 0 二进制补码：01111111 11111111 11111111 11111111 -> 1(转原码）

应用实际的代码进行验证：

#include
			int main()
{
     
	int a = -1;//00000000 00000000 00000000 00010000
	int b = a >> 1;// _0000000 00000000 00000000 00001000
	//_ 位置有两种方式填充 1.算术右移：补充符号位 2.逻辑右移：直接补0
	//注意计算机存储的是二进制补码 正数三码合一  负数的补码=反码+1 
	printf("%d\n", b);
	return 0;
}

说明这里是按照 算术移位 的方式来进行右移的

---

再举个例子 ：- 16
我们先按照算术移位的方式去推导最终结果，然后再修改变量大小成 - 16进行验证。


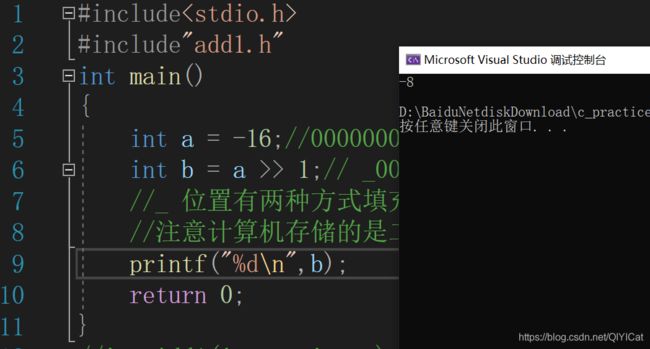
结果完全一样！ 经过推导这一步操作，我们能更加理解算术移位的方法，以及右操作符按照算术移位移动的方式。

正整数 16 >> 1 = 8 16 >> 2 = 4 可以发现右移移动一位相当于除以2 ，移动n位相当于除以2 ^ n。

警告：对于移位运算符，不要移动负数位，这个是标准未定义的。
eg： int num = 10；
num >> -1;//error

注意：移位操作符只能作用于整数，不能用于浮点数，因为浮点数的存储方式跟整数完全不同

---

三、位操作符

& （按位与） 二进制补码 两真才真（1） 一假则假（0）
| （按位或） 二进制补码 一真则真（1） 两假才假（0）
^ （按位异或） 二进制补码 相异为真（1） 相同为假（0）

#include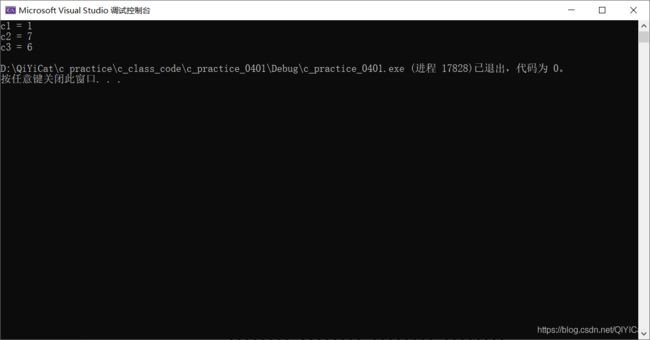
int main()
{
     
	int a = 3;        //00000000 00000000 00000000 00000011
	int b = 5;        //00000000 00000000 00000000 00000101
	int c1 = a & b;   //00000000 00000000 00000000 00000001  =1
	int c2 = a | b;   //00000000 00000000 00000000 00000111  =7
	int c3 = a ^ b;   //00000000 00000000 00000000 00000110  =6
	printf("c1 = %d\n", c1);
	printf("c2 = %d\n", c2);
	printf("c3 = %d\n", c3);
	return 0;
}

在求得 - 1的补码为 11111111 11111111 11111111 11111111 我们可以发现
-1 & i = i(i可为任何数）
-1 | i = -1(i可为任何数）

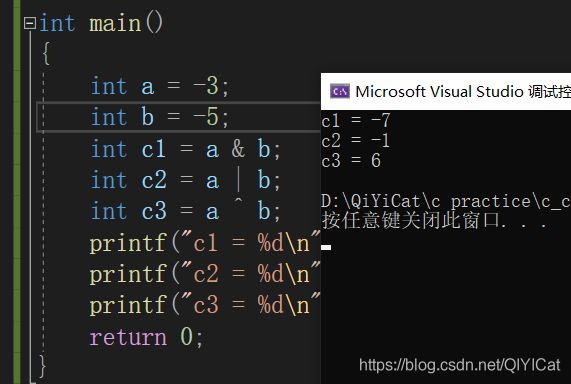
注意： ^ 操作符用来进行两个数的交换，不用创建第三个变量

---

练习举例1

XX公司面试真题：不能创建临时变量（第三个变量），实现两个数的交换。

假设我们给定两个数，a = 3, b = 5;

要实现两个数的交换，我们会想到醋和酱油交换的生活案例，我们会先找一个空瓶子，先将醋或者酱油倒到空瓶子中，（假设将醋先倒入空瓶子中）然后我们会将酱油倒入原醋瓶中，将原空瓶中的醋倒入酱油瓶中。
方法①根据这种方式，我们会先创建一个临时变量来用于两者的数值交换。

#include
int main()
{
     
	int a = 3;
	int b = 5;
	int temp = 0;
	printf("before:a = %d,b = %d\n", a, b);
	temp = a;
	a = b;
	b = temp;
	printf("after:a = %d,b = %d", a, b);
	return 0;
}

但是我们题目中明确要求不能创建变量，所以这种方式明显不合适。

这时候我们考虑另外一种方式，②从数学的角度出发：如果我先将 a与b之和放到a到当中 然后再用两者之和减去b不就得到a了吗，并把这个值赋给b，实现了a的值转移给b 。同理，用两者之和减去刚刚赋予a值到b中的b，就能得到原b的值（听起来有点绕是不，简单来说：就是 值：a + b - a = b = > 变量a

#include
//不创建临时变量实现两个数的交换
int main()
{
     
	//方法一：加减法
	int a = 3;
	int b = 5;
	printf("before:a = %d,b = %d\n", a, b);
	a = a + b;
	b = a - b;//将a的值给b
	a = a - b;//将b的值给a
	printf("after:a = %d,b = %d", a, b);
	return 0;
}

虽然上面说的这种方式实现了不用创建临时变量就交换两个数值，但是仍然存在一定的缺陷，比如我们的变量a, b并不等于3和5，而是一个很大或者离int边界阈值很接近的值，如果我们用两者相加的方法，a + b很有可能就超出int类型的边界阈值，得到一个并非我们想要的结果，再拿着这个结果去减去a或者b中一个数，并不能得到原本的另一个数的正确值。也就是存在“可能溢出”的缺陷。

③既然这种加减法因为阈值的问题存在缺陷，我们就要去考虑一种既能够成功交换两个数的值，还不会存在阈值的缺陷，更深层次的思考，数值的存储方式-- - 二进制，二进制能实现两者交换……a thousand years later—>异或操作符 ^ 这种位操作符不会产生进位的情况，所以不存在溢出的可能。

#include
//不创建临时变量实现两个数的交换
int main()
{
     
	int a = 3;
	int b = 5;
	printf("before:a = %d,b = %d\n", a, b);
	a = a ^ b;
	b = a ^ b;
	a = a ^ b;
	printf("after:a = %d,b = %d", a, b);
	return 0;
}

这里的 a^ b 可以看作一个密码 用这个密码去翻译（异或）b 可以得到a，用这个密码去翻译a，可以得到b
也就是 a^ b^ b = a a ^ b ^ a = b

总结：虽然方法3成功解决了不创建变量，实现两个数交换的问题，但是在实际使用中还是不建议使用方法3，这种方法一方面执行的效率低于方法1，另外一个方面也不便于阅读和理解。综合考虑，实际编写代码的时候，方法1最好。

---

练习举例2

编写代码实现：求一个整数存储在内存中的二进制中1的个数

①看到这个问题，我们可以想到利用整数求其二进制原码，只要在求的过程中判断余数是否为1，是就计数 + 1，根据这种想法，编写我的代码可以得到：

#include
int main()
{
     
	int a = 0;
	int count = 0;
	scanf("%d", &a);
	while (a)
	{
     
		if ((a % 2) == 1)
			count++;
		a = a / 2;
	}
	printf("count = %d\n", count);
	return 0;
}

这种方式看似正确，但是当我们输入负数的时候，比如 - 1， - 1补码为11111111 11111111 11111111 11111111 正确答案应该为：32 ，而我们程序运行却得到0。
（实际上这种方式还有补救方法，只要将 负数看作无符号位的整型，将a定义从 int a = 0; 成更改成unsigned int a - 1就会被当作一个超级大的数字11111111 11111111 11111111 11111111 来处理）

②既然这种方法不可行，我们就应该换一种思路，寻找新的方法，比如我能否得到输入数字存储的二进制补码，然后统计该补码中1的个数？答案是：可以，我们应该要想到任何一个数如果和 1进行按位与操作，若其最后一位数为1，则结果为1，若为0，结果为0。再借助移位操作符右移便可以统计1的个数（int类型的大小 为32位bit），因此可以编写代码为：

#include
int main()
{
     
	int a = 0;
	int count = 0;
	int i = 0;
	scanf("%d", &a);
	for (i = 0; i < 32; i++)
	{
     
		if (1 == ((a >> i) & 1))
		{
     
			count++;
		}
	}
	printf("count = %d\n", count);
	return 0;
}

这里我们的判断条件是：
if(1 == ((a >> i) & 1))
也可以更改为：
if((1 << i) == (a & (1 << i)))
或者 if (0！ = (a & (1 << i)))
或 if ((num & (1 << i)) != 0)
也就是将上面的1进行左移操作，然后将两者进行按位与操作，再比较1左移操作的结果 与按位与之后的结果是否相等，若相等，代表该二进制位置 为 1
但是这种写法比较复杂，可读性也比较差，建议仍然用if(1 == ((a >> i) & 1))这种方式。
这种方式虽然能够实现求二进制中1的个数，但是每次都需要循环32次，效率不太高。

③通过对输入数字的二进制操作，从最后一位1开始，每一步减少一个1

#include
int main()
{
     
	int a = 0;
	int count = 0;
	int i = 0;
	scanf("%d", &a);
	while (a)
	{
     
		count++;
		a &= a - 1;
		//a = a & (a - 1);
	}
	printf("count = %d\n", count);
	return 0;
}

a - 1能够让a的最后一位变成0 这种奇妙的感觉就像是三体小说中描写的“高维世界像低维世界塌陷”
有这样的一个公式 n & (n - 1)
假设n = 13 其后四位二进制补码为 1101

1101 ---- n
1100 ---- n - 1
1100 ---- n = n & (n - 1)
1011 ---- n - 1
1000 ---- n = n & (n - 1)
0111 ---- n - 1
0000 ---- n = n & (n - 1)

我们可以观察n的变化，发现每一次进行n = n & (n - 1)后，其最后一位的1（最右边的1）都会变成0（每执行一次，最右边的1都会消失，直到变成0，停止执行），那么在n变成0之前，n = n & (n - 1)能执行多少次，就代表最初的n中二进制补码就有多少个1。
这种算法的执行次数不用每次都执行32次，有多少个1，就执行多少次，所以效率很高！

注意：位操作符在进行运算的时候，不需要考虑符号位的影响，所有位都当做需要参与运算的二进制位，
比如 - 1 ^ -1 = 0, 即符号位也正常参与位操作符运算。

---

四、赋值操作符

①简单赋值操作符：
= 赋值操作符（注意：一个等号 = 表示赋值，两个等号 == 表示条件判断）
通过赋值操作符，我们可以给初始变量赋值，变更调整变量的值（也就是重新给变量赋值）
例如：

int weight = 80;//单位kg 
weight = 60;//对80不满意，重新赋值成60
double salary = 10000.0;
salary = 30000.0;//对salary只有10000.0不满意，变成30000.0
//赋值操作符也可以连续使用，比如
int a = 10;
int x = 0;
int y = 20;
a = x = y + 1; //连续赋值  //赋值操作符是从右往左计算的
//等同于：
x = y + 1;
a = x;

一般我们都是用分开的形式，不用连续赋值的形式，因为分开表示的方法更加容易阅读和理解，且易于调试。

②复杂赋值操作符
+= 、-= 、 *= 、 /=、 %= 、 >>=、 <<=、 &=、 |=、 ^=
举例：
int x = 10;
x = x + 10;
等同于：x += 10;

#include
int main()
{
     
	int a = 1;
	printf("%d\n", a += 1);
	printf("%d\n", a -= 1);
	printf("%d\n", a *= 2);
	printf("%d\n", a /= 2);
	printf("%d\n", a %= 2);
	printf("%d\n", a <<= 1);
	printf("%d\n", a >>= 1);
	printf("%d\n", a &= -1);
	printf("%d\n", a |= 1);
	printf("%d\n", a ^= 1);
	return 0;
}