机器学习实战二:波士顿房价预测 Boston Housing
波士顿房价预测 Boston housing
这是一个波士顿房价预测的一个实战,上一次的Titantic是生存预测,其实本质上是一个分类问题,就是根据数据分为1或为0,这次的波士顿房价预测更像是预测一个连续值,当然这也是一个非常经典的机器学习案例Boston housing
如果想了解更多的知识,可以去我的机器学习之路 The Road To Machine Learning通道
目录
- 活动背景
- 数据介绍
- 详细代码解释
-
- 导入Python Packages
- 读入数据 Read-In Data
- 从Package读取Boston数据
- 相关性检验
- 多变量研究
- 划分训练集和测试集
- 建立线性回归模型
-
- 评价模型
- 进一步探索和模型改进
-
- 特征选择重建模型
- 数据标准化
- 模型优化和改进
-
- GradientBoosting(梯度提升)
- Lasso 回归 (Least Absolute Shrinkage and Selection Operator)
- ElasticNet 回归
- Support Vector Regression (SVR)
-
- linear 线性核函数
- poly 多项式核
- rbf(Radial Basis Function) 径向基函数
- SVM(支持向量机)回归-- 线性核
- SVM(支持向量机)回归-- 多项式核
- 决策树回归
- 总结
活动背景
波士顿房地产市场竞争激烈,而你想成为该地区最好的房地产经纪人。为了更好地与同行竞争,你决定运用机器学习的一些基本概念,帮助客户为自己的房产定下最佳售价。幸运的是,你找到了波士顿房价的数据集,里面聚合了波士顿郊区包含多个特征维度的房价数据。你的任务是用可用的工具进行统计分析,并基于分析建立优化模型。这个模型将用来为你的客户评估房产的最佳售价。
数据介绍
详细代码解释
导入Python Packages
首先导入需要的python包
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
plt.style.use('ggplot')
%load_ext klab-autotime
读入数据 Read-In Data
将housing,csv读入
data = pd.read_csv('../data_files/2.Boston_housing/housing.csv')
data.info()
# No 属性 数据类型 字段描述x
# 1 CRIM Float 城镇人均犯罪率
# 2 ZN Float 占地面积超过2.5万平方英尺的住宅用地比例
# 3 INDUS Float 城镇非零售业务地区的比例
# 4 CHAS Integer 查尔斯河虚拟变量 (= 1 如果土地在河边;否则是0)
# 5 NOX Float 一氧化氮浓度(每1000万份)
# 6 RM Float 平均每居民房数
# 7 AGE Float 在1940年之前建成的所有者占用单位的比例
# 8 DIS Float 与五个波士顿就业中心的加权距离
# 9 RAD Integer 辐射状公路的可达性指数
# 10 TAX Float 每10,000美元的全额物业税率
# 11 PTRATIO Float 城镇师生比例
# 12 B Float 1000(Bk - 0.63)^ 2其中Bk是城镇黑人的比例
# 13 LSTAT Float 人口中地位较低人群的百分数
# 14 MEDV Float (目标变量/类别属性)以1000美元计算的自有住房的中位数


从这里可以看出来,数据一共有14个特征,并且没有缺失值,所以我们可以不用缺失值处理,真不错
从Package读取Boston数据
其实在我们的sklearn库中,就有波士顿房屋数据集,我们可以直接读取数据集
from sklearn.datasets import load_boston
dir(load_boston())
print(load_boston().DESCR)

这里也有对数据集详细的介绍,除此之外,我们还需要将数据集转化了类型,变为我们熟悉的pandas.core.frame.DataFrame,之后后面的操作就是一模一样的了
X = load_boston().data
y = load_boston().target
df = pd.DataFrame(X, columns=load_boston().feature_names)
df.head()
相关性检验
看看各个特征中是否有相关性,判断一下用哪种模型比较合适
plt.figure(figsize=(12,8))
sns.heatmap(data.corr(), annot=True, fmt='.2f', cmap='PuBu')
数据不存在相关性较小的属性,也不用担心共线性,所以我们可以用线性回归模型去预测
data.corr()['MEDV'].sort_values()
多变量研究
尝试了解因变量和自变量、自变量和自变量之间的关系
sns.pairplot(data[["LSTAT","RM","PIRATIO","MEDV"]])
划分训练集和测试集
由于数据没有null值,并且,都是连续型数据,所以暂时不用对数据进行过多的处理,不够既然要建立模型,首先就要进行对housing分为训练集和测试集,取出了大概百分之20的数据作为测试集,剩下的百分之70为训练集
X ,y = data[data.columns.delete(-1)], data['MEDV']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=888)
建立线性回归模型
首先,我利用线性回归模型对数据进行训练,并预测测试集数据,对于具体的线性回归的介绍,可以参考Linear Regression Machine Learning

linear_model = LinearRegression()
linear_model.fit(X_train, y_train)
coef = linear_model.coef_#回归系数
line_pre = linear_model.predict(X_test)
print('SCORE:{:.4f}'.format(linear_model.score(X_test, y_test)))
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y_test, line_pre))))
coef
根据结果来看,预测的score为76%左右,然后均方误差RMSE大约是4.5,为了更好的看出预测数据的问题,我想试着可视化一下

df_coef = pd.DataFrame()
df_coef['Title'] = data.columns.delete(-1)
df_coef['Coef'] = coef
df_coef
这是线性回归的相关系数
hos_pre = pd.DataFrame()
hos_pre['Predict'] = line_pre
hos_pre['Truth'] = y_test
hos_pre.plot(figsize=(18,8))
- 得出score为76%,从上图得知预测的房价整体偏小,在10-35这个区间预测结果较为准确,超过这个区间预测价格偏小,可进一步对原始数据离群值做处理。
- 数据比较干净,练习起来缺少特征工程部分的工作,而且是预测性模型,相比分类问题少了模型选择上的空间。
评价模型
在整个数据集上评价模型
plt.scatter(y_test, line_pre,label='y')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=4,label='predicted')
line_pre_all = linear_model.predict(X) #预测值
print('SCORE:{:.4f}'.format(linear_model.score(X,y)))
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y, line_pre_all))))
hos_pre_all = pd.DataFrame()
hos_pre_all['Predict'] = line_pre_all
hos_pre_all['Truth'] = y
hos_pre_all.plot(figsize=(18,8))
plt.scatter(y, line_pre_all,label='y')
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=4,label='predicted')
进一步探索和模型改进
- 尝试使用相关性最高的3个特征量重建模型,并与原模型进行比较
- 尝试使用其它多种算法分别建立模型,并比较模型
特征选择重建模型
首先我尝试相关性最高的三个特征重建模型,去与原模型比较一下
data.corr()['MEDV'].abs().sort_values(ascending=False).head(4)
由此我们得出了三个相关性最高的特征,我们将其作为自变量去建立模型

X2 = np.array(data[['LSTAT','RM','PIRATIO']])
X2_train, X2_test, y_train, y_test = train_test_split(X2, y, random_state=1,test_size=0.2)
linear_model2 = LinearRegression()
linear_model2.fit(X2_train,y_train)
print(linear_model2.intercept_)
print(linear_model2.coef_)
line2_pre = linear_model2.predict(X2_test) #预测值
print('SCORE:{:.4f}'.format(linear_model2.score(X2_test, y_test)))#模型评分
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y_test, line2_pre))))#RMSE(标准误差)
我们可以得到,对于预测测试集的数据的得分score明显是没有开始的线性回归模型1高的,然后我们再看看,在整个数据集中它的表现

line2_pre_all = linear_model2.predict(X2) #预测值
print('SCORE:{:.4f}'.format(linear_model2.score(X2, y)))#模型评分
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y, line2_pre_all))))#RMSE(标准误差)

这样比较下来,第一个模型达到的分数,即使在整个数据集中73%,但是这个模型的得分大约是67.6%,由此可以得出,第一个模型还是比这个模型优的,接下来就需要尝试更多的模型了
数据标准化
数据集的 标准化 对scikit-learn中实现的大多数机器学习算法来说是 常见的要求 。如果个别特征或多或少看起来不是很像标准正态分布(具有零均值和单位方差),那么它们的表现力可能会较差。
所以我这里首先对数据进行了一个标准化处理
from sklearn.preprocessing import StandardScaler
ss_x = StandardScaler()
X_train = ss_x.fit_transform(X_train)
X_test = ss_x.transform(X_test)
ss_y = StandardScaler()
y_train = ss_y.fit_transform(y_train.values.reshape(-1, 1))
y_test = ss_y.transform(y_test.values.reshape(-1, 1))
模型优化和改进
接下来我就开始尝试多种模型,希望尝试的模型有对我的算法有帮助
X ,y = data[data.columns.delete(-1)], data['MEDV']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=9)
GradientBoosting(梯度提升)
from sklearn import ensemble
#params = {'n_estimators': 500, 'max_depth': 4, 'min_samples_split': 1,'learning_rate': 0.01, 'loss': 'ls'}
#clf = ensemble.GradientBoostingRegressor(**params)
clf = ensemble.GradientBoostingRegressor()
clf.fit(X_train, y_train)
clf_pre=clf.predict(X_test) #预测值
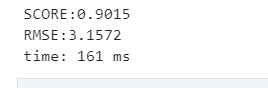
print('SCORE:{:.4f}'.format(clf.score(X_test, y_test)))#模型评分
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y_test, clf_pre))))#RMSE(标准误差)
Lasso 回归 (Least Absolute Shrinkage and Selection Operator)
Lasso也是惩罚其回归系数的绝对值。
与岭回归不同的是,Lasso回归在惩罚方程中用的是绝对值,而不是平方。这就使得惩罚后的值可能会变成0
from sklearn.linear_model import Lasso
lasso = Lasso()
lasso.fit(X_train,y_train)
y_predict_lasso = lasso.predict(X_test)
r2_score_lasso = r2(y_test,y_predict_lasso)
print('SCORE:{:.4f}'.format( lasso.score(X_test, y_test)))#模型评分
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y_test,y_predict_lasso))))#RMSE(标准误差)
print('Lasso模型的R-squared值为:',r2_score_lasso)
ElasticNet 回归
ElasticNet回归是Lasso回归和岭回归的组合
enet = ElasticNet()
enet.fit(X_train,y_train)
y_predict_enet = enet.predict(X_test)
r2_score_enet = r2(y_test,y_predict_enet)
print('SCORE:{:.4f}'.format( enet.score(X_test, y_test)))#模型评分
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y_test,y_predict_enet))))#RMSE(标准误差)
print("ElasticNet模型的R-squared值为:",r2_score_enet)
Support Vector Regression (SVR)
from sklearn.linear_model import ElasticNet
from sklearn.svm import SVR
from sklearn.metrics import confusion_matrix, classification_report
from sklearn.metrics import r2_score as r2, mean_squared_error as mse, mean_absolute_error as mae
def svr_model(kernel):
svr = SVR(kernel=kernel)
svr.fit(X_train, y_train)
y_predict = svr.predict(X_test)
# score(): Returns the coefficient of determination R^2 of the prediction.
print(kernel,' SVR的默认衡量评估值值为:', svr.score(X_test,y_test))
print(kernel,' SVR的R-squared值为:', r2(y_test, y_predict))
print(kernel,' SVR的均方误差(mean squared error)为:',mse(y_test, y_predict))
print(kernel,' SVR的平均绝对误差(mean absolute error)为:',mae(y_test,y_predict))
# print(kernel,' SVR的均方误差(mean squared error)为:',mse(scalery.inverse_transform(y_test), scalery.inverse_transform(y_predict)))
# print(kernel,' SVR的平均绝对误差(mean absolute error)为:',mae(scalery.inverse_transform(y_test),scalery.inverse_transform(y_predict)))
return svr
linear 线性核函数
linear_svr = svr_model(kernel='linear')
poly 多项式核
poly_svr = svr_model(kernel='poly')
rbf(Radial Basis Function) 径向基函数
rbf_svr = svr_model(kernel='rbf')
SVM(支持向量机)回归-- 线性核
from sklearn.svm import SVR
linear_svr = SVR(kernel="linear")
linear_svr.fit(X_train, y_train)
linear_svr_pre = linear_svr.predict(X_test)#预测值
print('SCORE:{:.4f}'.format(linear_svr.score(X_test, y_test)))#模型评分
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y_test, linear_svr_pre))))#RMSE(标准误差)
SVM(支持向量机)回归-- 多项式核
在使用SVM回归-- 多项式核的时候,首先要对数据进行一个标准化处理
from sklearn.preprocessing import StandardScaler
ss_x = StandardScaler()
X_train = ss_x.fit_transform(X_train)
X_test = ss_x.transform(X_test)
ss_y = StandardScaler()
y_train = ss_y.fit_transform(y_train.values.reshape(-1, 1))
y_test = ss_y.transform(y_test.values.reshape(-1, 1))
再进行建立模型来预测
poly_svr = SVR(kernel="poly")
poly_svr.fit(X_train, y_train)
poly_svr_pre = poly_svr.predict(X_test)#预测值
print('SCORE:{:.4f}'.format(poly_svr.score(X_test, y_test)))#模型评分
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y_test, poly_svr_pre))))#RMSE(标准误差)
决策树回归
from sklearn.tree import DecisionTreeRegressor
tree_reg=DecisionTreeRegressor(max_depth=2)
tree_reg.fit(X_train, y_train)
tree_reg_pre = tree_reg.predict(X_test)#预测值
print('SCORE:{:.4f}'.format( tree_reg.score(X_test, y_test)))#模型评分
print('RMSE:{:.4f}'.format(np.sqrt(mean_squared_error(y_test,tree_reg_pre))))#RMSE(标准误差)
最后我们会发现,利用GBDT的得分居然高达90,这是我们得到最优的一个模型了,其次就是SVR回归的多项式核,也大概达到了85,其他的并没有线性回归那么优,所以对于波士顿房价预测来说,利用GBDT是最好的,这是迄今为止我遇到最好的模型
总结
- 可以发现,如果要用Gradient Boosting 算法的话,在sklearn包里调用是非常方便的,几行代码即可完成,大部分的工作是在数据特征提取
- 数据分析过程中,特征设计是最重要的,现在kaggle竞赛很流行使用GBDT(梯度提升决策树Gradient Boosted Decision Tree) 算法,数据分析结果的优劣其实主要在特征上,行业中做项目也是如此
- 不断的在研究数据中培养对数据的敏感度十分重要
每日一句
Never had to laugh at other people.(没经历过才笑别人的疤)
如果需要数据和代码,可以自提
- 路径1:我的gitee
- 路径2:百度网盘
链接:https://pan.baidu.com/s/1uA5YU06FEW7pW8g9KaHaaw
提取码:5605