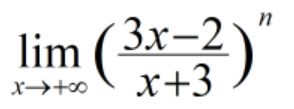高等数学基于Python的实现

一元函数微分的Python实现

变量与函数

1、Python标识符和关键字

Python标识符就是程序员定义的变量名和函数名

Phon标识符的命名规则

1. 必须是不含空格的单个词;
2. 区分大小写;
3. 必须以字母或下划线开头,之后可以是任意字母、数字或下划线,变量名
   中不允许使用标点符号

Python关键字

Python关键字就是在 Python内部已经使用的标识符，具有特殊的功能和含义，Python不允许定义和关键字有相同名字的标识符。Python常见关键字表如下：

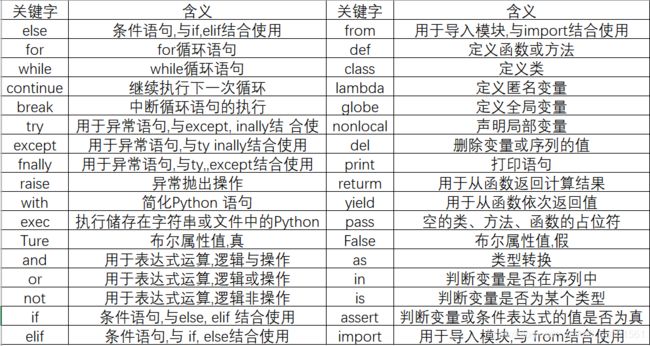
2、变量赋值

Python语句由表达式和变量组成,变量赋值通常有以下几种形式
(1)单个变量赋值:变量=表达式
其中，“=”为赋值符号，将右边表达式的值赋给左边变量
(2)同步赋值：变量1,变量2,…,变量n=表达式1，表达式2，…，表达式n。
**例如：**将1314赋值给变量X，将hello赋值给变量Y。
解：在IDLE中按如下操作

>>>x,y=1314,"hello"  #将1314赋值给变量X，将hello赋值给变量Y
>>>x,y               #按enter键，该指令被执行

命令窗口显示所得结果

（1314，“hello")

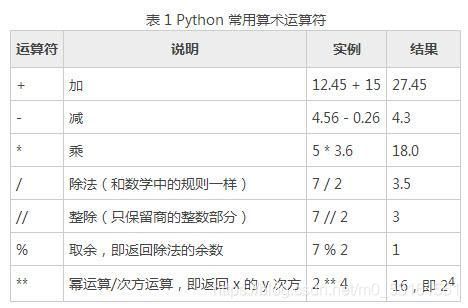
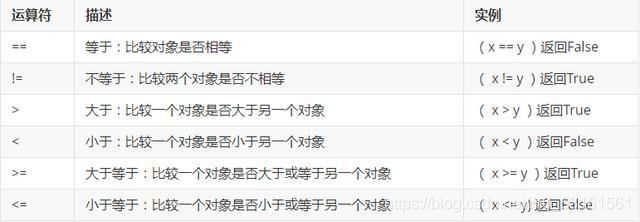
3、Python基本运算符

算术运算符

比较运算符

Python函数

math标准库中常用数学函数

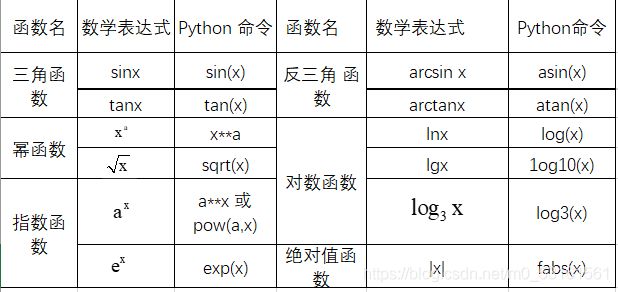
例如：调用math标准库，计算sin90
解：在IDLE中按如下操作

>>>import math       #导入math标准库
>>>math.sin(math.pi/2)   #调用math标准库中的sin()函数和pi值

命令窗口显示所得结果

1.0

4、利用Python绘制平面曲线

Python第三方库Matplotlib的命令——plot()绘图函数
plot(x,y):若x和y为长度相等的数组，则绘制以x和y分别为横、纵坐标的二维曲线。
plot()是绘制二维曲线的函数，但在使用此函数之前，需先定义曲线上每一点的x及y的坐标。
ps：利用Python绘制平面曲线，首先需安装第三方库Matplotlib，否则无法实现图像。

例题与演示

例1：
解：在pycharm中新建文件，内容如下：

import matplotlib.pyplot as plt
from numpy import *
x = arange(0,2*pi,0.01)  #利用numpy库中的arange（）函数定义区间之间公差为0.01的数组
y = sin(x)
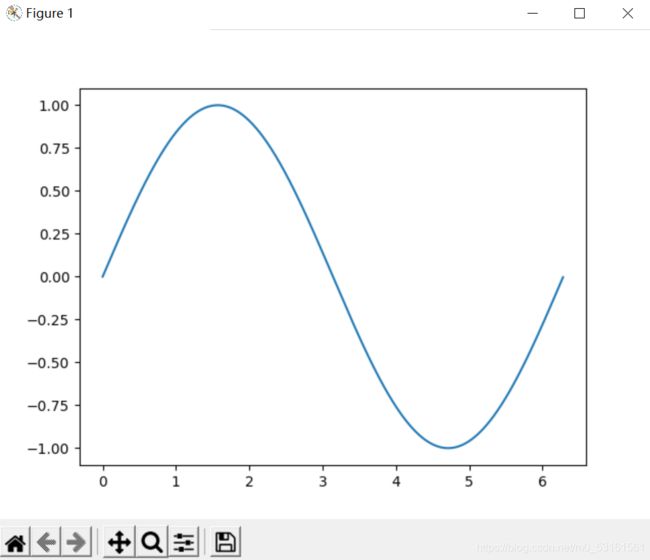
plt.figure()            #在绘制窗口开始绘图
plt.plot(x,y)
plt.show()

运行程序如下：

例2：绘制y=sinx+cosx+1的图像，判断其奇偶性，并观察在x=0处的连续性。

解：在pycharm中新建文件，内容如下：

import matplotlib.pyplot as plt
from numpy import *
x = arange(-5,5,0.01)  #利用numpy库中的arange（）函数定义区间之间公差为0.01的数组
y = sin(x)+cos(x)+1
plt.figure()            #在绘制窗口开始绘图
plt.plot(x,y)
plt.axis([-6,6,-3,3])      #设置坐标范围
plt.grid(True)          #制定网格线
plt.show()

运行程序如下：

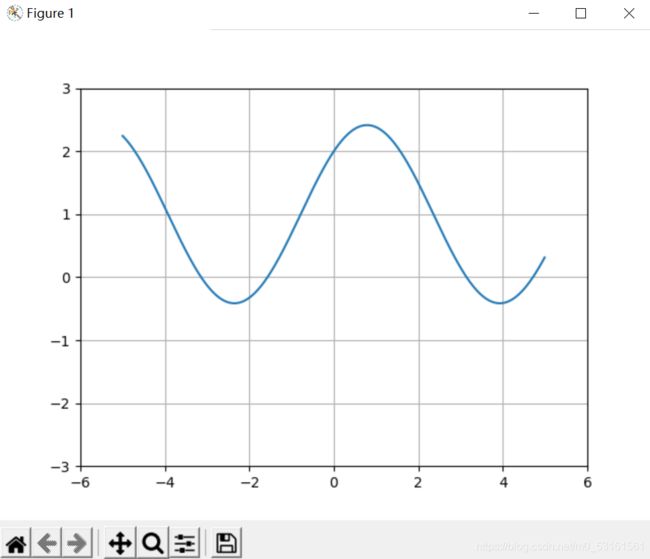
由图可知，y=sinx+cosx+1是非奇非偶函数，在x=0处连续。

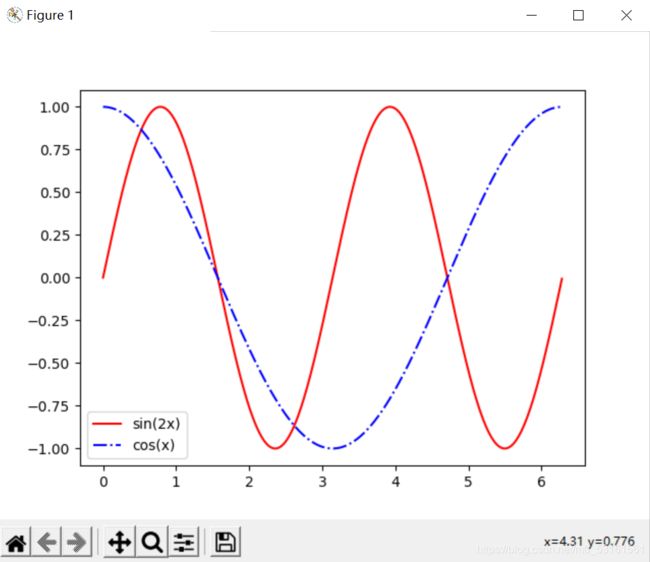
例3：在同一坐标上绘制函数y=cosx和y=sinx的图像
解：在pycharm中新建文件，内容如下：

import matplotlib.pyplot as plt
from numpy import *
x = arange(0,2*pi,0.01)  #利用numpy库中的arange（）函数定义区间之间公差为0.01的数组
y1 = sin(2*x)
y2 = cos(x)
plt.figure()            #在绘制窗口开始绘图
plt.plot(x,y1,color="r",linestyle="-",label="sin(2x)")  #可以控制颜色和线型
plt.plot(x,y2,color="b",linestyle="-.",label="cos(x)")  #plt.plot(x,y1,x,y2)可以输出两条曲线
plt.legend()   #显示图像
plt.show()

运行程序如下：

5、求解函数极限

sympy标准库中求极限的常用函数

例题与演示

例4：求下列极限

解：在pycharm中新建文件，内容如下：

from sympy import *
x,n=symbols('x n')#symbols()函数用于初始化多个变量
print(limit(((3*x-2)/(x+3))**3,x,oo))

运行程序，命令窗口显示所得结果：

3**n

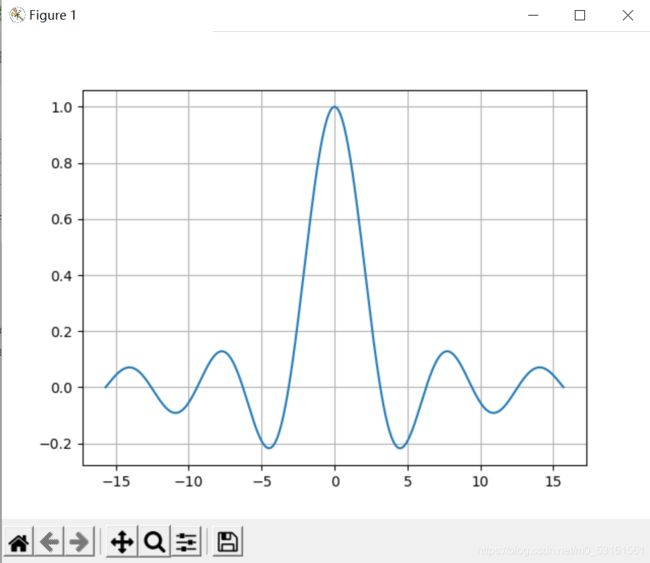
例5：考察f(x)=sinx/x在x-0时的变化趋势，并求极限
解：在pycharm中新建文件，内容如下：

import matplotlib.pyplot as  plt
from numpy import *
x=arange(-5*pi,5*pi,0.01)
y=sin(x)/x
plt.figure()
plt.plot(x,y)
plt.grid(True)
plt.show()

运行程序，命令窗口显示所得结果：

由图可知，f(x）在x=0附近连续变化，其值与1无限靠近，可见该极限为1.