拉普拉斯变换
阅读本文之前,建议先阅读我的另一篇文章《傅里叶级数与傅里叶变换公式推导》,这是本文的基础。
另外可参考视频【中文翻译配音】3D动画详细解释傅里叶与拉普拉斯变换! 以及 珂学原理」No. 26「拉普拉斯变换了什么 以及 傅里叶变换的直观解释
拉普拉斯变换和傅里叶变换的联系
首先,列出傅里叶变换的公式:
F ( ω ) = ∫ − ∞ ∞ f ( t ) e − i ω t d t F(ω) = \int_{-\infty}^{\infty} f(t) e^{-i\omega t}dt F(ω)=∫−∞∞f(t)e−iωtdt
变换条件:狄利克雷条件,通俗来说,没办法表示一些持续递增的函数,因此会导致 ∫ − ∞ ∞ f ( t ) e − i ω t d t \int_{-\infty}^{\infty} f(t) e^{-i\omega t}dt ∫−∞∞f(t)e−iωtdt的结果趋于无穷。
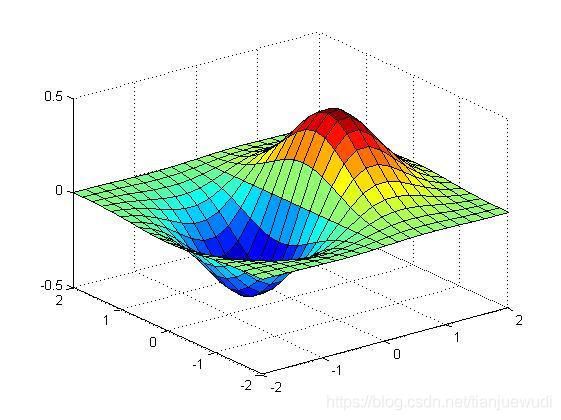
这时,我们对 f ( t ) f(t) f(t)先进行处理,乘上一个衰减因子 e − σ t ( σ > 0 ) e^{-\sigma t}(\sigma>0) e−σt(σ>0),使其在无穷远处衰减为0。式子变为:
F ( ω ) = ∫ − ∞ ∞ f ( t ) e − ( i ω + σ ) t d t F(ω) = \int_{-\infty}^{\infty} f(t) e^{-(i\omega+\sigma) t}dt F(ω)=∫−∞∞f(t)e−(iω+σ)tdt
L ( s ) = ∫ 0 ∞ f ( t ) e − s t d t L(s) = \int_{0}^{\infty} f(t) e^{-st}dt L(s)=∫0∞f(t)e−stdt
这里我们在工程上只考虑t=0之后的信号变换,因此积分下限为0。并且可以理解为把原函数分解为了 e σ t sin ω x e^{\sigma t}\sin\omega x eσtsinωx和 e σ t sin ω x e^{\sigma t}\sin\omega x eσtsinωx的形式,这样就能解决函数无穷远处无穷大的问题。即傅里叶变换是一个正弦扫描器,而拉普拉斯变换是一个正弦和指数扫描器。
其中截取其中的 σ = 0 \sigma = 0 σ=0的平面就是傅里叶变换的函数。
拉普拉斯变换的收敛域
收敛域的定义:在收敛域中,存在 σ \sigma σ,使得 f ( t ) e − σ t f(t)e^{-\sigma t} f(t)e−σt为收敛函数,从使得 ∫ − ∞ ∞ f ( t ) e − ( i ω + σ ) t \int_{-\infty}^{\infty} f(t) e^{-(i\omega+\sigma) t} ∫−∞∞f(t)e−(iω+σ)t收敛。
也就是说,当 σ \sigma σ足够大使得 f ( t ) e − σ t f(t)e^{-\sigma t} f(t)e−σt在无穷远处收敛为0时,此处为收敛域,当 σ \sigma σ小于某一个阈值时为发散域。
通常我们非常关注拉普拉斯变换的极点,这时拉普拉斯变换的作用就体现出来了。很多系统,例如RLC电路,弹簧上的质量,以及普遍的控制系统会产生正弦和指数输出,因此需要比傅里叶变换更强大的工具去分析它们。极点的实部就代表了函数包含的指数项,虚部代表函数包含的三角函数项的频率。在自动控制系统中,出现了虚轴往右的极点,即代表有不衰减甚至增大的信号,系统不稳定。
拉普拉斯变换的应用
常用拉普拉斯变换公式
L ( e − a t ) = ∫ 0 ∞ e − a t e − s t d t = − 1 a + s e − ( a + s ) t ∣ 0 ∞ = 1 a + s \mathscr{L}(e^{-at}) = \int_{0}^{\infty} e^{-at} e^{-st}dt = -\frac 1 {a+s}e^{-(a+s)t}|_0^{\infty} = \frac 1 {a+s} L(e−at)=∫0∞e−ate−stdt=−a+s1e−(a+s)t∣0∞=a+s1
L ( u ( t ) ) = 1 s \mathscr{L}(u(t)) = \frac 1 s L(u(t))=s1
L ( δ ( t ) ) = ∫ 0 + ∞ δ ( t ) e − s t d t = 1 \mathscr{L}(\delta(t)) = \int_0^{+\infty} \delta(t)e^{-st}dt = 1 L(δ(t))=∫0+∞δ(t)e−stdt=1
L ( t ) = 1 s 2 \mathscr{L}(t) = \frac 1 {s^2} L(t)=s21
L ( t 2 2 ) = 1 s 2 \mathscr{L}(\frac {t^2} 2) = \frac 1 {s^2} L(2t2)=s21
L ( t n n ! ) = 1 s n + 1 \mathscr{L}(\frac {t^n} {n!}) = \frac 1 {s^{n+1}} L(n!tn)=sn+11
L ( t e − a t ) = 1 ( s + a ) 2 \mathscr{L}(te^{-at}) = \frac 1 {(s+a)^2} L(te−at)=(s+a)21
L ( s i n ω t ) = ω s 2 + ω 2 \mathscr{L}(sinωt) = \frac ω {s^2+ω^2} L(sinωt)=s2+ω2ω
L ( c o s ω t ) = s s 2 + ω 2 \mathscr{L}(cosωt) = \frac s {s^2+ω^2} L(cosωt)=s2+ω2s
L ( e − a t s i n ω t ) = ω ( s + a ) 2 + ω 2 \mathscr{L}(e^{-at}sinωt) = \frac ω {(s+a)^2+ω^2} L(e−atsinωt)=(s+a)2+ω2ω
L ( e − a t c o s ω t ) = s + a ( s + a ) 2 + ω 2 \mathscr{L}(e^{-at}cosωt) = \frac {s+a} {(s+a)^2+ω^2} L(e−atcosωt)=(s+a)2+ω2s+a
性质
拉普拉斯变换是线性变换,也就是说符合叠加原理:
L ( a f ( t ) + b g ( t ) ) = a F ( s ) + b G ( s ) \mathscr{L}(af(t) + bg(t)) = aF(s)+bG(s) L(af(t)+bg(t))=aF(s)+bG(s)
求导:
L ( f ′ ( t ) ) = ∫ 0 + ∞ f ′ ( t ) e − s t d t = f ( t ) e − s t ∣ 0 + ∞ − ∫ 0 + ∞ f ( t ) ( − s e − s t ) d t = s F ( s ) − f ( 0 ) = s F ( s ) \mathscr{L}(f'(t))= \int_0^{+\infty}f'(t)e^{-st}dt = f(t)e^{-st}|_0^{+\infty} -\int_0^{+\infty}f(t)(-se^{-st})dt = sF(s)-f(0)=sF(s) L(f′(t))=∫0+∞f′(t)e−stdt=f(t)e−st∣0+∞−∫0+∞f(t)(−se−st)dt=sF(s)−f(0)=sF(s)
同理,积分:
L ( ∫ 0 t f ( t ) d t ) = F ( s ) s \mathscr{L}(\int_0^t f(t)dt) = \frac {F(s)} s L(∫0tf(t)dt)=sF(s)
卷积:
L ( f ( t ) ⊗ g ( t ) ) = F ( s ) G ( s ) \mathscr{L}(f(t)\otimes g(t)) = F(s)G(s) L(f(t)⊗g(t))=F(s)G(s)
这些在解微分方程(描述动态世界的数学手段)等方面大大简化了运算,因此拉普拉斯变换是方便快捷的分析工具。
拉普拉斯逆变换
公式:
L − 1 ( F ( s ) ) = 1 2 π i ∫ c − j ∞ c + j ∞ F ( s ) e s t d s L^{-1}(F(s)) = \frac 1 {2\pi i}\int_{c-j\infty}^{c+j\infty}F(s)e^{st}ds L−1(F(s))=2πi1∫c−j∞c+j∞F(s)estds
但这个公式在我们的学习过程中并不常用,通常可以用我们上面的常用拉普拉斯变换公式来推导出逆变换结果。