如何简单形象又有趣地讲解神经网络是什么?
神经网络的出现可追溯到20世纪40年代,因此,其有相当长的发展历史。本书将介绍神经网络的发展历史,因为你需要了解一些术语。激活函数是其中一个很好的例子,它可以缩放神经网络中神经元的值。阈值激活函数是研究人员引入了神经网络时的早期选择,而后S型激活函数、双曲正切激活函数、修正线性单元(Rectified Linear Unit,ReLU)激活函数等相继被提出。虽然目前大多数文献都建议仅使用ReLU激活函数,但你需要了解S型激活函数和双曲正切激活函数,才能理解ReLU激活函数的优势。
只要有可能,我们就会指出要使用神经网络的哪个架构组件。我们总是会将现在大家接受的架构组件指定为推荐选择,而不是较早的经典组件。我们将许多这些架构组件放在一起,并在第14章“构建神经网络”中为你提供一些有关构建神经网络的具体建议。
在神经网络的发展历程中,神经网络曾几次从灰烬中重生。McCulloch W.和Pitts W.(1943)首先提出了神经网络的概念。但是,他们没有方法来训练这些神经网络。程序员必须手工制作这些早期神经网络的权重矩阵。由于这个过程很烦琐,因此神经网络首次被弃用了。
Rosenblatt F.(1958)提出了一种训练算法,即反向传播算法,该算法可自动创建神经网络的权重矩阵。实际上,反向传播算法有许多神经元层,可模拟动物大脑的结构,但是,反向传播算法的速度很慢,并且会随着层数的增加变得更慢。从20世纪80年代到20世纪90年代初期计算能力的增加似乎有助于神经网络执行任务,但这个时代的硬件和训练算法无法有效地训练多层神经网络,神经网络又一次被弃用了。
神经网络的再次兴起,是因为Hinton G.(2006)提出了一种全新的深度神经网络训练算法。高速图形处理单元(Graphics Processing Unit,GPU)的最新进展,使程序员可以训练具有三层或更多层的神经网络。程序员逐步意识到深层神经网络的好处,从而促使该技术重新流行。
神经网络逻辑
作为计算机程序员,你可能熟悉逻辑编程。你可以使用编程运算符AND、OR和NOT来控制程序的决策方式。这些逻辑运算符通常定义了神经网络中权重和偏置的实际含义。考虑以下真值表:
0 AND 0 = 0
1 AND 0 = 0
0 AND 1 = 0
1 AND 1 = 1
0 OR 0 = 0
1 OR 0 = 1
0 OR 1 = 1
1 OR 1 = 1
NOT 0 = 1
NOT 1 = 0真值表指定如果AND运算符的两边均为真,则最终输出也为真。在所有其他情况下,AND的结果均为假。这个定义非常适合英文单词“and”。如果你想要一栋风景宜人“且”有大后院的房子,那么这个房子必须同时满足这两个条件才能选择。如果你想要一间视野开阔“或”后院很大的房子,那么这个房子只需要满足一个条件就可以了。
这些逻辑语句可能变得更加复杂。请考虑如果你想要一间视野开阔且后院很大的房子,但是,你对后院较小但在公园附近的房子也会感到满意。你可以通过以下方式表示这一想法:
([nice view] AND [large yard]) OR ((NOT [large yard]) and [park])你可以使用以下逻辑运算符来表示前面的语句:
![]()
(1-9)
在上面的语句中,OR(
![]()
看起来像字母“v”,AND(
![]()
)看起来像颠倒的“v”,而NOT(
![]()
)看起来像半个方框。
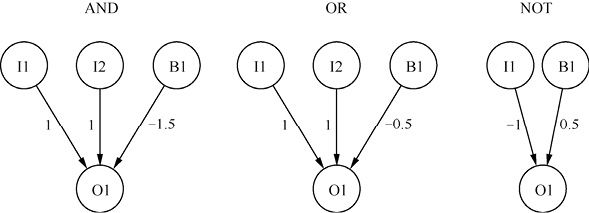
我们可以使用神经网络来表示AND、OR和NOT的基本逻辑运算符,如图1-14所示。
图1-14展示了3个基本逻辑运算符的权重和偏置权重。你可以用公式1-1轻松计算所有这些运算符的输出。请考虑具有两个“真”(1)输入的AND运算符:
(1 * 1) + (1 * 1) + (−1.5) = 0.5
图1-14 基本逻辑运算符
这里我们用的是阶跃激活函数。因为0.5大于或等于0.5,所以输出为1,即真。我们可以计算一个输入为假的表达式:
(1 * 1) + (0 * 1) + (−1.5) = −0.5由于我们采用阶跃激活函数,因此这个输出为0,即假。
我们可以利用这些神经元构建更复杂的逻辑结构。考虑具有以下真值表的异或运算符:
0 XOR 0 = 0
1 XOR 0 = 1
0 XOR 1 = 1
1 XOR 1 = 0XOR运算符规定,它的一个输入(但不是两个输入)为真时,结果为真。如两辆车中的一辆将赢得比赛,但并非两辆都获胜。可以使用基本的AND、OR和NOT运算符编写XOR运算符,如下所示:
![]()
(1-10)
带圆圈的加号是XOR运算符的符号,
![]()
和
![]()
是要评估的两个输入。如果你明白XOR运算符的含义是
![]()
或
![]()
,但不是同时
![]()
和
![]()
,那么上述表达式的意义就清楚了。图1-15展示了可以表示XOR运算符的神经网络。
图1-15 XOR神经网络
计算上述神经网络需要几个步骤。首先,必须为每个直接连接到输入的节点计算值。上述神经网络有两个节点。我们将展示用输入[0,1]来计算XOR的例子。我们首先计算两个最上面的未标记(隐藏)节点:
(0 * 1) + (1 * 1) − 0.5 = 0.5 = True
(0 * 1) + (1 * 1) − 1.5 = −0.5 = False接下来,我们计算未标记(隐藏)的下部节点:
(0 * −1) + 0.5 = 0.5 = True最后,我们计算O1:
(1 * 1) + (1 * 1) −1.5 = 0.5 = True如你所见,你可以手动连接神经网络中的连线以产生所需的输出,但是,手动创建神经网络非常烦琐。
如果要从头开始学习神经网络,那么可以看一看《人工智能算法(卷3):深度学习和神经网络》(Artificial Intelligence for Humans, Volume 3: Deep Learning and Neural Networks)
从书中你可以学到这些知识
- 神经网络基础
- 自组织映射
自从Pitts(1943)引入神经网络以来,人们已经发明了许多不同的神经网络类型。我们主要集中在仍有相关性的经典神经网络上,这些神经网络为我们在本书后续内容中介绍的其他架构奠定了基础。
本章重点介绍了SOM,它是可以对数据进行聚类的无监督神经网络。SOM的输入神经元个数等于要进行聚类的数据的属性数。输出神经元个数等于应将数据聚类到的组数。SOM以无监督的方式进行训练。换言之,其只有数据点被提供给神经网络,没有提供预期的输出。SOM学习对数据点进行聚类,尤其是与训练过的数据点相似的数据点。
- 霍普菲尔德神经网络和玻尔兹曼机
我们将研究另外两种经典的神经网络:霍普菲尔德神经网络和玻尔兹曼机。这两种神经网络有些相似,因为它们在训练过程中都使用能量函数。能量函数测量神经网络中的能量。随着训练的进行,能量将随着神经网络的学习而减少。
- 前馈神经网络
“前馈”一词描述了该神经网络如何处理和记忆模式。在前馈神经网络中,神经网络的每一层都包含到下一层的连接。如这些连接从输入向前延伸到隐藏层,但是没有向后的连接。这种安排不同于第3章中介绍的霍普菲尔德神经网络。霍普菲尔德神经网络是完全连接的,它的连接既向前又向后。在后文,我们将分析前馈神经网络的结构及其记忆模式的方式。
我们可以使用多种反向传播算法中的各种技术来训练前馈神经网络,这是一种有监督的训练形式,我们将在第5章中进行详细讨论。本章重点介绍应用优化算法来训练神经网络的权重。如果你需要有关优化算法的更多信息,本系列图书的卷1和卷2包含相关内容。尽管可以用几种优化算法来训练权重,但我们主要将注意力集中在模拟退火上。
优化算法会调整一个数字向量,旨在根据一个目标函数获得良好的得分。目标函数基于该神经网络的输出与预期输出的匹配程度,为神经网络提供得分。该得分允许用任何优化算法来训练神经网络。
前馈神经网络类似于我们已经探讨过的神经网络。其从一个输入层开始,可能连接到隐藏层或输出层。如果连接到隐藏层,则该隐藏层可以随后连接到另一个隐藏层或输出层。隐藏层可以有任意多层。
- 训练与评估
由于神经网络可以通过许多不同的方式进行训练与评估,因此我们需要一种一致的方法来对它们进行判断。目标函数评估神经网络并返回得分,训练会根据得分调整神经网络,以便取得更好的结果。通常,目标函数希望得分较低,其试图获得较低得分的过程称为最小化。你可能会设定最大化的问题,此时目标函数需要较高的得分。因此,你可以将大多数训练算法用于最小化或最大化问题。
你可以使用任何连续的优化算法来优化神经网络的权重,如模拟退火、粒子群优化(Particle Swarm Optimization,PSO)、遗传算法、爬山、Nelder-Mead或随机行走等。本章将介绍模拟退火,它是一种简单的训练算法。但是,除了优化算法外,你还可以利用反向传播算法训练神经网络。在第6章“反向传播训练”和第7章“其他传播训练”中将介绍几种算法,它们都基于第6章介绍的反向传播训练算法。
- 反向传播训练
反向传播是训练神经网络的最常用方法之一。Rumelhart、Hinton和Williams(1986)引入了反向传播,该方法到今天仍然很流行。程序员经常使用反向传播训练深层神经网络,因为在图形处理单元上运行时,它的伸缩性很好。要了解这种用于神经网络的算法,我们必须探讨如何训练它,以及它如何处理模式。
经典的反向传播已得到扩展和修改,产生了许多不同的训练算法。本章中将讨论神经网络最常用的训练算法。
- 其他传播训练
反向传播算法影响了许多训练算法,如第6章介绍的SGD。对于大多数训练,SGD算法和Nesterov动量是训练算法的不错选择。但是,还有其他选择。在本章中,我们研究两种受反向传播思想启发的流行算法。
要使用这两种算法,你无须了解它们实现的每个细节。本质上,这两种算法都可以实现与反向传播相同的目标。因此,你可以在大多数神经网络框架中用它们代替反向传播或SGD。如果发现SGD不收敛,就可以转向弹性传播(Resilient backPROPagation,RPROP)或莱文伯格-马夸特算法(Levenberg-Marquardt Algorithm;LM算法,LMA)以进行实验。
- NEAT、CPPN和HyperNEAT
NEAT是一种通过遗传算法进化神经网络结构的算法。CPPN是一种进化的神经网络,可以创建其他结构,如图像或其他神经网络。Hypercube-based NEAT或HyperNEAT(一种CPPN)也进化出其他神经网络。HyperNEAT训练了这些神经网络后,就可以在它们的尺寸上轻松处理更高的分辨率。
许多不同的框架都支持NEAT和HyperNEAT。对于Java和C#,我们建议使用自己的Encog实现。你可以在Kenneth Stanley的网站上找到NEAT实现的完整列表和HyperNEAT实现的完整列表。
- 深度学习
深度学习是神经网络编程中相对较新的进展,它代表了一种训练深度神经网络的方法。本质上,任何具有两层以上的神经网络都是深度神经网络。自从Pitts(1943)引入多层感知机(multilayer perceptron)以来,我们就已经具备创建深度神经网络的能力。但是,直到Hinton(1984)成为第一个成功训练这些复杂神经网络的研究者之后,我们才能够有效地训练神经网络。
- 卷积神经网络
CNN是一种神经网络技术,它已深刻地影响了计算机视觉领域。Fukushima(1980)引入了卷积神经网络的原始概念,LeCun、Bottou、Bengio和Haffner(1998)大大改进了这个概念。通过这项研究,Yann LeCun引入了著名的LeNet-5神经网络架构。本章介绍具有LeNet-5风格的卷积神经网络。
尽管主要是在计算机视觉领域使用CNN,但该技术在这个领域之外也有一些应用。你需要认识到,如果要在非可视数据上使用CNN,则必须找到一种对数据进行编码的方法,让它可以模拟可视数据的属性。
CNN有点类似于我们在第2章“自组织映射”中讨论的SOM。向量元素的顺序对训练至关重要。相比之下,大多数不是CNN或SOM的神经网络都将其输入数据看成值的长向量,在这个向量中传入特征的排列顺序是无关紧要的。对于这些类型的神经网络,训练神经网络后就无法更改传入特征的排列顺序。换言之,CNN和SOM不遵循输入向量的标准处理。
SOM将输入排列成网格。这种安排对图像效果很好,因为互相邻近的像素对彼此很重要。显然,图像中像素的顺序很重要。人体就是这类顺序的一个相关例子——对于脸部的设计,我们习惯于眼睛彼此靠近。同样地,类似SOM的神经网络坚持这样的像素顺序。因此,它们在计算机视觉领域中有许多应用。
尽管SOM和CNN相似,都采用了将输入映射到2D网格,甚至更高维度的对象(如3D盒子)的方式,但CNN将图像识别提升到了更高的水平。CNN的这一进步缘于对生物眼睛的多年研究。换言之,CNN利用重叠的输入视野(field)来模拟生物眼睛的特征。在这项突破之前,人工智能一直无法复制生物视觉的功能。
过去,缩放、旋转和噪声为AI计算机视觉研究带来了挑战。在下面的例子中,你可以看到生物眼睛的复杂性。一个朋友举起一张纸,上面写着一个很大的数字。当你的朋友离你越来越近时,这个数字仍然可以被识别。当你的朋友旋转纸张时,你仍然可以识别该数字。最后,你的朋友通过在纸上画上线条,产生噪声,你仍然可以识别该数字。如你所见,这些例子演示了生物眼睛的高级功能,让你可以更好地了解CNN的研究突破。也就是说,在计算机视觉领域,该神经网络能处理缩放、旋转和噪声。
- 剪枝和模型选择
剪枝通过分析每个神经元对神经网络输出的贡献来进行。如果特定神经元与另一神经元的连接不会显著影响神经网络的输出,则删除该连接。通过这个过程,对输出仅产生少量影响的连接和神经元将被删除。
本章介绍的另一种算法是模型选择。剪枝从已经训练好的神经网络开始,而模型选择会创建并训练许多具有不同超参数的神经网络。然后,程序选择产生神经网络的超参数,以达到最佳验证得分。
- Dropout和正则化
程序员经常参加认证考试,以证明他们在给定编程语言上的能力。为了帮助程序员准备这些考试,测试者通常会提供模拟考试。考虑一个程序员,他开始不停地参加模拟考试:学习更多内容,然后参加认证考试。在某个时候,程序员已经记住了很多模拟考试题,而不是学习解决单个问题所必需的技术。现在程序员已经对模拟考试产生了过拟合。当该程序员参加实际考试时,他的实际分数可能会比他在模拟考试中获得的分数低。
一台计算机也可能过拟合。尽管神经网络在其训练数据上得分很高,但是这个结果并不意味着同一神经网络在训练集以外的数据上得分很高。正则化是可以减少过拟合的技术之一。存在许多不同的正则化技术,它们大多数的工作方式是分析,并可能修改神经网络在训练时的权重。
- 时间序列和循环神经网络
一周中温度的变化是时间序列数据的一个例子。如果我们知道今天的温度是25摄氏度,明天的温度是27摄氏度,那么循环神经网络和时间序列编码提供了另一种选择来预测一周中的正确温度。相反,对于给定的输入,传统的前馈神经网络将始终以相同的输出进行响应。如果前馈神经网络经过训练可以预测明天的温度,那么它对25的响应应该为27。即当给出25时,它会始终输出27,这一事实可能会妨碍它进行预测。当然,27摄氏度的温度不会总是跟随着25摄氏度。神经网络最好考虑到要预测的这一天的前几天的温度,也许上周的气温能帮助我们更准确地预测明天的温度。因此,循环神经网络和时间序列编码代表两种不同的方法,来解决随时间推移表示神经网络数据的问题。
到目前为止,我们研究过的神经网络始终具有前向连接。输入层始终连接到第一个隐藏层,每个隐藏层始终连接到下一个隐藏层,最终的隐藏层始终连接到输出层。这种连接层的方式是将这些神经网络称为“前馈”的原因。循环神经网络没有那么严格,因为其允许反向连接。循环连接将一层中的神经元连接到上一层或神经元本身。大多数循环神经网络架构都在循环连接中保持状态。前馈神经网络不保持任何状态。循环神经网络的状态充当了神经网络的一种短期记忆,因此,循环神经网络对于给定的输入将不会总是产生相同的输出。
- 构建神经网络
我们将通过两种方式提出架构建议。第一种方式,我们会报告AI领域的科学文献的建议。这些建议包括引文,以便你查看原始论文。但是,我们会努力以一种通俗易懂的方式介绍论文的关键概念。第二种方式,我们将通过实验,运行几种竞争的架构,并报告结果。
要记住,一些明确而固定的规则,并不能决定每个项目的最佳架构。每个数据集都是不同的,每个数据集的最佳神经网络也是不同的。
- 可视化
常常有人问我们以下有关神经网络的问题:“我已经构建了一个神经网络,但是当我训练它时,错误率永远达不到可接受的水平。我该怎么办?”调查的第一步是确定是否发生以下常见错误:
- 正确的输入和输出神经元数量;
- 数据集正确归一化;
- 神经网络的一些致命设计决策。
显然,你必须具有正确数量的输入神经元,以匹配数据的标准化方式。同样,对于回归问题,你应该有单个输出神经元;对于分类问题,通常应该对每个类别都有一个输出神经元。你应该规范化输入数据,以使其适合你使用的激活函数。类似的致命错误,如没有隐藏层,或学习率为0,可能会造成糟糕的情况。
在排除了所有这些错误后,就必须查看数据。对于分类问题,你的神经网络可能难以区分某些分类。为帮助你解决这个问题,有一些可视化算法,可让你查看神经网络可能遇到的问题。本章中介绍的两种可视化技术将揭示以下数据问题:
- 容易与其他分类混淆的分类;
- 带噪声的数据;
- 分类之间的差异。
我们将在后续内容中描述每个问题,并提供一些可能的解决方案。通过两种复杂性递增的算法,我们将介绍这些潜在的解决方案。可视化主题不仅对数据分析很重要,也是本书的读者选择的主题,本书通过Kickstarter活动获得了最初的资助。本项目最初的653个支持者从多个有竞争力的项目主题中选择了可视化。因此,我们将展示两种可视化。这两个示例都将使用本书前面几章研究过的MNIST手写数字数据集。
- 用神经网络建模
黑客技能本质上是计算机编程的子集。尽管数据科学家不一定需要IT专业人员的基础结构知识,但是这些技术、技能让他们能够创建简短、有效的程序来处理数据。在数据科学领域,信息处理称为数据整理。
数学和统计知识涵盖统计、概率和其他推理方法。实质性知识描述了业务知识,以及对实际数据的理解。如果仅将这些主题中的两个结合在一起,你就不会拥有数据科学的所有组件,如图16-1所示。换言之,数学和统计知识实质性专业知识的结合只是传统研究。仅有这两项技能并不足以完全包含数据科学所需的能力(即机器学习)。
也可以选择这本
Python神经网络编程
如果你可以进行加、减、乘、除运算,那么你就可以制作自己的神经网络。我们使用的最困难运算是梯度演算(gradient calculus),但是,我们会对这一概念加以说明,使尽可能多的读者能够理解这个概念。
有兴趣的读者,不妨以本书为起点,进一步探索激动人心的人工智能。一旦你掌握了神经网络的基本知识,你就可以将神经网络的核心思想运用到许多不同的问题中。
在这本书中,我们将扬帆起航,制作神经网络,识别手写数字。
我们将从非常简单的预测神经元开始,然后逐步改进它们,直到达到它们的极限。顺着这条路,我们将做一些短暂的停留,学习一些数学概念。我们需要这些数学概念来理解神经网络如何学习和预测问题的解。
我们将浏览一些数学思想,如函数、简单的线性分类器、迭代细化、矩阵乘法、梯度演算、通过梯度下降进行优化,甚至是几何旋转。但是,所有这些数学概念将会以一种非常优雅清晰的方式进行解释,并且除了简单的中学数学知识以外,读者完全不需要任何前提知识或专业技术。
一旦我们成功制作了第一个神经网络,我们将带着这种思想,在各个方面使用这种思想。例如,我们无需诉诸额外的训练数据,就可以使用图像处理来改善机器学习。我们将一窥神经网络的思想,看看它是否揭示了任何深刻的见解——很多书籍并没有向你展示神经网络的工作机制。
当我们循序渐进制作神经网络时,我们还将学习一种非常简单、有用和流行的编程语言Python。同样,你不需要有任何先前的编程经验。