DES加密算法原理及代码实现
目录
一、简要描述
二、名词解释
数据填充
分组加密
算法特点
置换
三、加密运算
1、加密运算流程图
2、初始置换
3、生成子秘钥
PC-1置换
PC-2置换
4、迭代的过程(f函数)
f函数
E-盒扩展
S-盒替代
P-盒置换
左右交换
5、逆置换
四、解密流程
五、代码实现
六、数据填充
七、总结
一、简要描述
DES 算法是一种常见的分组加密算法,由IBM公司在1971年提出。DES 算法是分组加密算法的典型代表。其加密运算、解密运算使用相同的秘钥。
DES 算法利用56+8奇偶校验位(第8,16,24,32,40,48,56,64)=64位的密钥对以64位为单位的块数据进行加解密。
二、名词解释
数据填充
DES算法是以64位为一组分组加密的,所以当输入的明文长度,不满足64的整数倍时,需要涉及到数据的填充
分组加密
DES算法将输入明文分为N个64位大小的分组,然后依次根据加密运算,生成N组加密后的密文 ,将生成的N组密文,就是我们要最终的成果——DES密文输出
算法特点
使用56位的密钥(一般密钥说是64位,实际上有效位只有56位,其余8位是校验位)
以64位位单位,对数据分组进行加密和解密(密文与明文长度相同,均为64位)。
DES加密与解密使用同一密钥(属于对称加密)
DES的保密性依赖于密钥。(DES的加密算法是公开的,密钥是保密的)
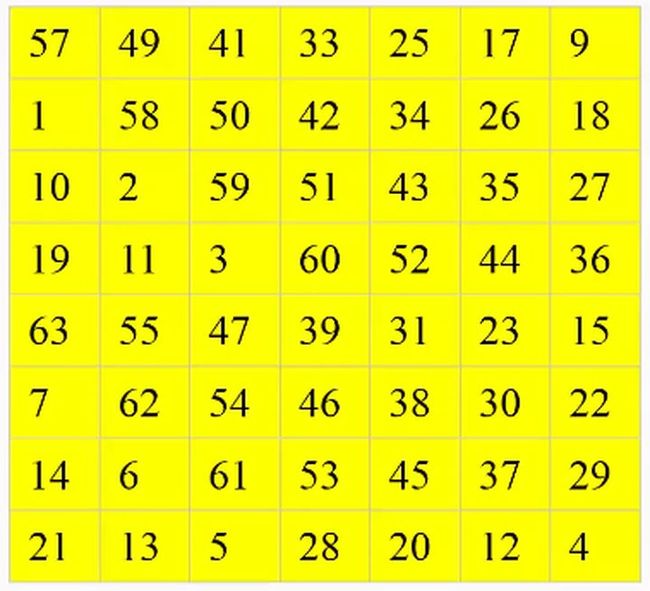
置换
可以简单的理解为将 【将明文打乱】 ——将分组后的64位二进制明文重新排序。这个重排序的过程就是移位,不同的置换中,有不同的移位规则。具体的规则我们可以参照置换表。置换表如下图:
解释一下,置换表的读取顺序是从上到下,由左至右。
第一位 58 , 意思是 将原明文的第58位移动至第一位
第二位 50 , 意思是将原明文的第50位之冬至第二位
依次类推
三、加密运算
1、加密运算流程图
以下加密流程,明文M是指的输入明文中的一个分组。
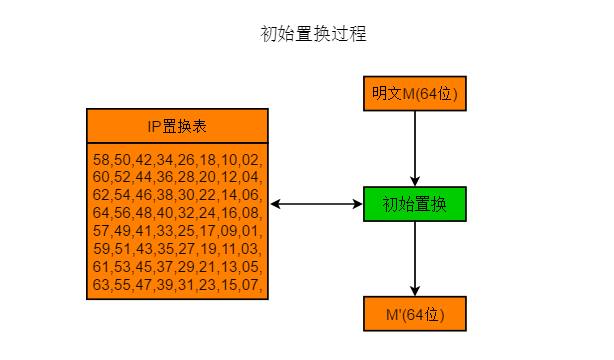
2、初始置换
初始置换就是将明文M打乱重排序。并生成L0 , R0。
输入64位明文数据M(64位):
明文M(64位)=
0110001101101111011011010111000001110101011101000110010101110010
M经过IP置换后为M'
M'(64位)=
1111111110111000011101100101011100000000111111110000011010000011
取M'的前32位作为L0,则有
L0(32位)= 11111111101110000111011001010111
取M'的后32位作为R0,则有
R0(32位)= 00000000111111110000011010000011
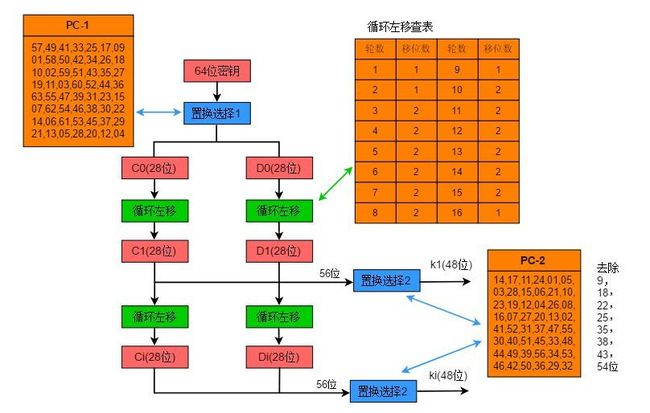
3、生成子秘钥
DES加密的过程,明文M共经历了16次运算迭代,每次迭代的数据长度是48 ,因此我们需要16组48位的加密秘钥来进行加密。
PC-1置换
我们知道秘钥的长度是64 (58位真实秘钥 + 8位奇偶校验位) , PC-1置换就是剔除掉奇偶校验位,并打乱用户秘钥的的过程。
PC-1表为8行7列的表,密钥K经PC-1后变为56位数据K'。
K'(56位)= 11110000110011001010101011110101010101100110011110001111
取K'的前28位作为C0,则有
C0(28位)= 1111000011001100101010101111
取K'的后28位作为D0,则有
D0(28位)= 0101010101100110011110001111
下来依次是C1,D1为C0,D0左移一位,C2,D2为C1,D1左移一位,C3,D3为C2,D2左移两位.......
所以,可以得到C1D1----C16D16的结果为:
C1 = 1110000 1100110 01010101011111
D1 = 1010101011001100111100011110
C2 = 1100001100110010101010111111
D2 = 0101010110011001111000111101
C3 = 0000110011001010101011111111
D3 = 0101011001100111100011110101
................
.................
C15 = 1111100001100110010101010111
D15 = 1010101010110011001111000111
C16 = 1111000011001100101010101111
D16 = 0101010101100101101110001111
PC-2置换
PC-1置换后生成了(CnDn)共16组56位的二进制字符,PC-2置换就是根据公式Kn(48位) = PC-2(CnDn(56位))再次进行置换,生成16组子秘钥
C1(28位)= 1110000 1100110 0101010 1011111
D1(28位)= 1010101 0110011 0011110 0011110
C1和D1合并后为56位,经过PC-2表置换得到密钥K1(48位)
K1(48位)= 000110110000001011101111111111000111000001110010
并依次获取K2,K3,K4,K5,K6,K7,K8,K9,K10,K11,K12,K13,K14,K15,K16
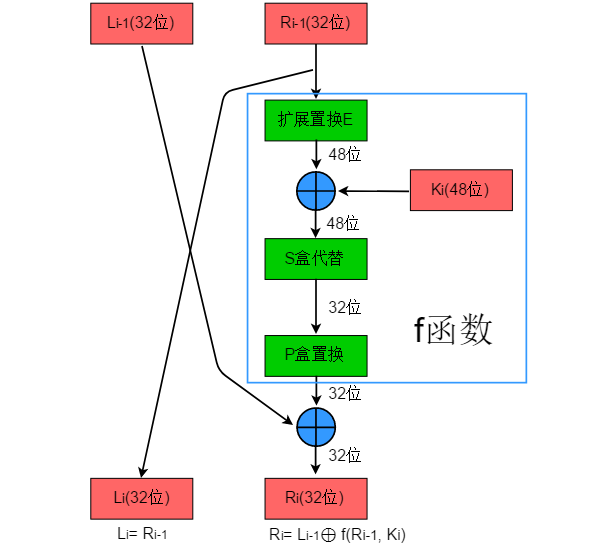
4、迭代的过程(f函数)
f函数
f函数就是不断计算Li,Ri的过程,此过程包括四个部分:E盒置换、S盒置换、P盒置换、左右校验,我们简要的总结如下:
E-盒扩展
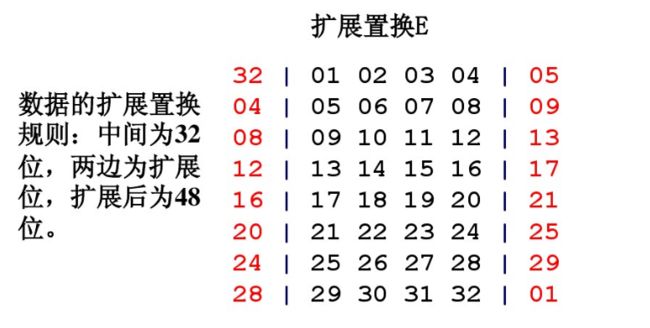
通过扩展置换E,数据的右半部分Rn从32位扩展到48位。扩展置换改变了位的次序,重复了某些位。
扩展置换的目的:
a、产生与秘钥相同长度的数据以进行异或运算,R0是32位,子秘钥是48位,所以R0要先进行扩展置换之后与子秘钥进行异或运算;
b、提供更长的结果,使得在替代运算时能够进行压缩。
扩展置换E规则如下:
例子:
L0(32位)= 11111111101110000111011001010111
R0(32位)= 00000000111111110000011010000011
R0(32位)经过扩展置换后变为48位数据:
E(R0)(48位)= 100000000001011111111110100000001101010000000110
将E(R0)(48位)与K1(48位)作异或运算
100000000001011111111110100000001101010000000110
XOR
000110110000001011101111111111000111000001110010
= 100110110001010100010001011111001010010001110100
得到:
E(R0)^K1(48位)= 100110110001010100010001011111001010010001110100
S-盒替代
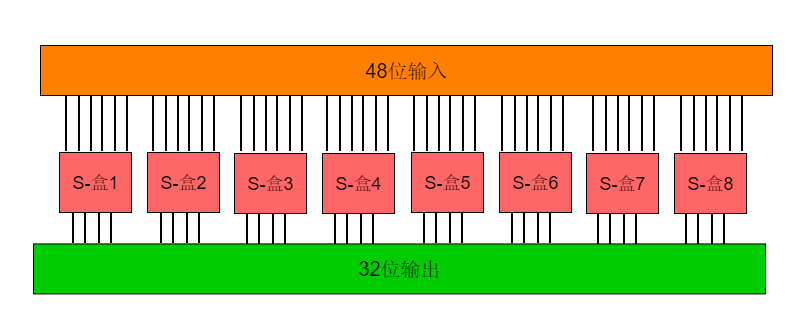
S盒替代简而言之就是“6进4出”的。(传入S盒的是6位数据,从S盒输出的是4位数据),将E盒输出的48位替换压缩为32位。
Rn扩展置换之后与子秘钥Kn异或以后的结果En作为输入块进行S盒代替运算功能是把48位数据变为32位数据。代替运算由8个不同的代替盒(S盒)完成。每个S-盒有6位输入,4位输出。所以48位的输入块被分成8个6位的分组,每一个分组对应一个S-盒代替操作。经过S-盒代替,形成8个4位分组结果。
注意:每一个S-盒的输入数据是6位,输出数据是4位,但是每个S-盒自身是64位!!每个S-和是4行16列的格式,因为二进制4位是0~15。
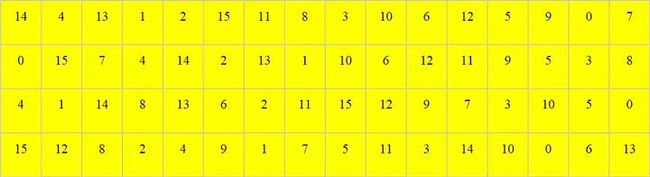
S盒的计算规则:
例如:若S-盒1的输入为110111,第一位与最后一位构成11,十进制值为3,则对应第3行,中间4位为1011对应的十进制值为11,则对应第11列。查找S-盒1表的值为14,则S-盒1的输出为1110。8个S盒将输入的48位数据输出为32位数据。
S-盒1 至 S-盒8不再一一列举
例子:
按照S-盒的计算过程,将
E(R0)^K1(48位)= 100110110001010100010001011111001010010001110100,通过 S- 盒替换得到的S盒输出为10001011110001000110001011101010(32位)。
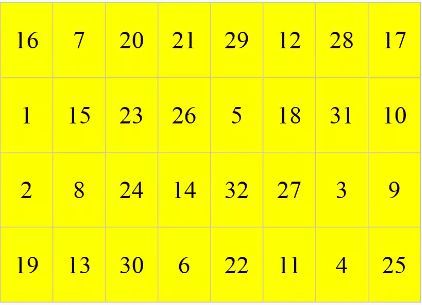
P-盒置换
P盒置换是32位的输入移位转换成32位的输出。其具体过程同IP置换,不再赘述。
例子:
将S盒输出10001011110001000110001011101010(32位)
经过P盒置换,P-盒置换输出 0100 1000 1011 1111 0101 0101 1000 0001
将此结果与 L0(32位) = 1111 1111 1011 1000 0111 0110 0101 0111
进行异或运算得到结果为: 1011 0111 0000 0111 0010 0011 1101 0110
左右交换
将上述结果赋值给R1
将R0原封不动的赋值给L1
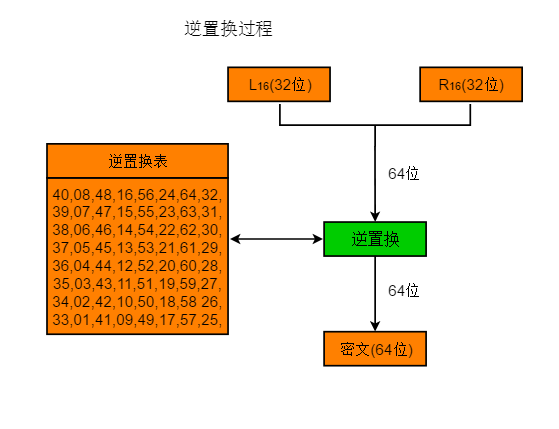
5、逆置换
将f函数的过程使用k1-k16,迭代16次,即经过16次的交换替代,得到L16 、R16,并将此作为输入进行逆置换得到最后的密文,逆置换的过程同初始置换,不再赘述。
例子:
将L16与R16构成64位数据,经过逆置换表输出密文为:
密文:0101100000001000001100000000101111001101110101100001100001101000
四、解密流程
解密过程同加密过程,只不过是按照反向的次序即可。
五、代码实现
package com.general.encryanddecode;
import org.omg.PortableInterceptor.SYSTEM_EXCEPTION;
import java.util.Arrays;
/**
* @author hee-wong
*
* 根据DES算法原理实现DES加密算法,主要是为了更加深入地理解DES算法
* **/
public class CustomDES {
//初始置换
private int[] IP={58,50,42,34,26,18,10,2,
60,52,44,36,28,20,12,4,
62,54,46,38,30,22,14,6,
64,56,48,40,32,24,16,8,
57,49,41,33,25,17,9,1,
59,51,43,35,27,19,11,3,
61,53,45,37,29,21,13,5,
63,55,47,39,31,23,15,7};
//逆初始置换
private int[] IP_1={40,8,48,16,56,24,64,32,
39,7,47,15,55,23,63,31,
38,6,46,14,54,22,62,30,
37,5,45,13,53,21,61,29,
36,4,44,12,52,20,60,28,
35,3,43,11,51,19,59,27,
34,2,42,10,50,18,58,26,
33,1,41,9,49,17,57,25};//手残,数组数据没写全
//E扩展
private int[] E={32,1,2,3,4,5,
4,5,6,7,8,9,
8,9,10,11,12,13,
12,13,14,15,16,17,
16,17,18,19,20,21,
20,21,22,23,24,25,
24,25,26,27,28,29,
28,29,30,31,32,1};
//P置换
private int[] P={16,7,20,21,29,12,28,17,
1,15,23,26,5,18,31,10,
2,8,24,14,32,27,3,9,
19,13,30,6,22,11,4,25};
private static final int[][][] S_Box = {
{
{ 14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7 },
{ 0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8 },
{ 4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0 },
{ 15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13 } },
{
{ 15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10 },
{ 3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5 },
{ 0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15 },
{ 13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9 } },
{
{ 10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8 },
{ 13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1 },
{ 13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7 },
{ 1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12 } },
{
{ 7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15 },
{ 13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9 },
{ 10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4 },
{ 3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14 } },
{
{ 2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9 },
{ 14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6 },
{ 4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14 },
{ 11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3 } },
{
{ 12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11 },
{ 10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8 },
{ 9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6 },
{ 4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13 } },
{
{ 4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1 },
{ 13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6 },
{ 1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2 },
{ 6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12 } },
{
{ 13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7 },
{ 1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2 },
{ 7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8 },
{ 2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11 } }
};
//PC-1
private int[] PC1={57,49,41,33,25,17,9,
1,58,50,42,34,26,18,
10,2,59,51,43,35,27,
19,11,3,60,52,44,36,
63,55,47,39,31,23,15,
7,62,54,46,38,30,22,
14,6,61,53,45,37,29,
21,13,5,28,20,12,4};
//PC-2
private int[] PC2={14,17,11,24,1,5,3,28,
15,6,21,10,23,19,12,4,
26,8,16,7,27,20,13,2,
41,52,31,37,47,55,30,40,
51,45,33,48,44,49,39,56,
34,53,46,42,50,36,29,32};
//Schedule of Left Shifts
private int[] LFT={1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1};
/**加密轮数**/
private static final int LOOP_NUM=16;
private String [] keys=new String[LOOP_NUM];
private String [] pContent;
private String [] cContent;
private int origin_length;
/**16个子密钥**/
private int[][] sub_key=new int[16][48];
private String content;
private int p_origin_length;
public CustomDES(String key,String content){
this.content=content;
p_origin_length=content.getBytes().length;
generateKeys(key);
}
public static void main(String[] args){
String origin="试试能跑通吗";
System.out.println("原文:\n"+origin);
CustomDES customDES=new CustomDES("密码学专栏",origin);
byte[] c=customDES.deal(origin.getBytes(),1);
System.out.println("密文:\n"+new String(c));
byte[]p=customDES.deal(c,0);
byte[] p_d=new byte[origin.getBytes().length];
System.arraycopy(p,0,p_d,0,origin.getBytes().length);
System.out.println("明文:\n"+new String(p));
}
/****拆分分组****/
public byte[] deal(byte[] p ,int flag){
origin_length=p.length;
int g_num;
int r_num;
g_num=origin_length/8;
r_num=8-(origin_length-g_num*8);//8不填充
byte[] p_padding;
/****填充********/
if (r_num<8){
p_padding=new byte[origin_length+r_num];
System.arraycopy(p,0,p_padding,0,origin_length);
for(int i=0;i -1; i--) {
L(p_IP, i, flag, k[i]);
}
}
int[] c=new int[64];
for(int i=0;i 六、数据填充
当明文长度不为分组长度的整数倍时,需要在最后一个分组中填充一些数据使其凑满一个分组长度。
NoPadding
API或算法本身不对数据进行处理,加密数据由加密双方约定填补算法。例如若对字符串数据进行加解密,可以补充\0或者空格,然后trim
PKCS5Padding
加密前:数据字节长度对8取余,余数为m,若m>0,则补足8-m个字节,字节数值为8-m,即差几个字节就补几个字节,字节数值即为补充的字节数,若为0则补充8个字节的8
解密后:取最后一个字节,值为m,则从数据尾部删除m个字节,剩余数据即为加密前的原文。
加密字符串为为AAA,则补位为AAA55555;加密字符串为BBBBBB,则补位为BBBBBB22;加密字符串为CCCCCCCC,则补位为CCCCCCCC88888888。
PKCS7Padding
PKCS7Padding 的填充方式和PKCS5Padding 填充方式一样。只是加密块的字节数不同。PKCS5Padding明确定义了加密块是8字节,PKCS7Padding加密快可以是1-255之间。
七、总结
DES 加密算法为最为常见的分组加密算法。其主要思想在于数据位的置换与移位过程,通过16次的迭代加密与最终的逆置换得出最终的密文。DES 的解密方式只需按照加密的逆过程求解即可。由于DES 加密过程的算法是公开的,所以密钥K的保密就显得尤为重要,只有发送方与接收方采用相同的密钥进行加密解密才能获取明文数据。