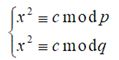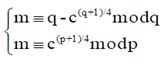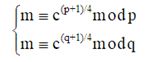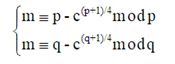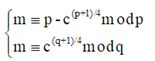Abstract:文中对于公钥密码体制的研究与发展进行了介绍,其中着重介绍了几个比较常用的公钥密码体制RSA,EIGamal
Keywords: 公钥密码体制,RSA,离散对数问题
1. 引言
公钥密码体制又称公开密钥密码体系,公钥密码体制是现代密码学的最重要的发明和进展,在1976年,Whitfield Diffie和Martin Hellman发表了“New directions in cryptography”这篇划时代的文章奠定了公钥密码系统的基础。在公钥密码体制之中,加密密匙和解密密匙是不一样的,无法通过加密密匙的反推得到解密密匙,所以加密密匙是可以公开的,并且不会危及密码体制的安全性。因为对称密钥密码体制有一个缺点是必须要在Alice和Bob之间首先在传输密文之前使用一个安全信道交换密钥。实际上,这是很难达到的,而公钥密码体制改善了这一点,Alice可以利用公钥加密规则发出一条加密的消息给Bob,Bob是唯一能够运用解密规则对其解密的人,例如保险箱的传递,只有接收的人知道密码并且能够打开。【1】要在自从公钥密码的概念被提出以来,相继提出了许多公钥密码方案,如RSA、ElGamal、基于离散对数问题的公钥密码体制等[2]。
2. 预备知识
公钥密码的理论基础,在公钥密码中,加密密钥和解密密钥是不一样的,加密密钥为公钥,解密密钥为私钥。一个问题是难解的,直观上讲,就是不存在一个计算该问题的有效算法,也可称之为按照目前的计算能力,无法在一个相对的短时间内完成,即解决这个问题所付出的成本远远超过了解决之后得到的结果,计算应一个难解的问题所需要的时间一般是以输入数据长度的指数函数形式递增,所以随着输入数据的增多,复杂度会急剧的增大,对于一个问题,如果存在一个求其解的有效算法,则称其为有效问题,否则为无效问题。在公钥密码机制之中,进行破译已经加密后的密码应该是一个难解问题。
公钥密码的理论基础是陷门单向函数:
定义2.1:设f是一个函数,如果对于任意给定的x,计算y=f(x)是容易的,但对于任意给定的y,计算f(x)=y是难解的,则称f是一个单向函数。
例子
定义2.2:设f是一个函数,t是与f有关的一个参数,对任意给定的x,计算y使得y=f(x)是容易的,如果当不知参数t时,计算f的逆函数是难解的,但当知道参数t时,计算f的逆函数是容易的,则称f是一个陷门单向函数(trapdoor one-way function),参数t称为陷门。
在公钥密匙中,加密变换是一个陷门单向函数,只带陷门的人可以容易的进行解密变换,而不知道陷门的人则无法有效的进行解密变换。
3. 公钥密码方案
3.1 RSA公钥密码
当前最著名、应用最广泛的公钥系统 RSA 是在 1978 年由美国麻省理工学院的 Rivest 、 Shamir 和 Adleman 提出的, 它是一个基于数论的非对称密码体制, 是一种分组密码体制。 RSA 算法是第一个既能用于数据加密也能用于数字签名的算法。公钥加密算法中使用最广的是RSA。
RSA使用一个公钥,一个私钥。公钥加密,私钥解密,密钥长度从40到2048bit可变,加密时也把明文分成块,块的大小可变,但不能超过密钥的长度,RSA算法把每一块明文转化为与密钥长度相同的密文块。密钥越长,加密效果越好,但加密解密的开销也大,所以要在安全与性能之间折衷考虑,一般64位是较合适的。RSA的一个比较知名的应用是SSL,在美国和加拿大SSL用128位RSA算法,由于出口限制,在其它地区(包括中国)通用的则是40位版本。
RSA的安全性基本大于大整数的因子分解,其基础是数论中的欧拉定理。因子分解可以破解RSA密码系统,但是目前尚无人证明RSA的解密一定需要分解因子。
RSA密钥生成过程:1)选取两个大素数p,q; 2)乘积 n = pq, Φ(n) = (p-1)(q-1),其中Φ(n)为n的欧拉函数;3)随机选取整数e(1
RSA加密过程:,明文先转换为比特串分组,使每个分组对应的十进制数小于n,即分组长度小于n,即分组长度小于,然后对每个明文分组mi作加密运算,具体过程:1)获取公钥(e,n);2)把消息M分组长度为L(L<)的消息分组M=m1m2……mn;3)使用加密算法,计算出密文c.
RSA解密过程:将密文c按长度L分组得c=c1c2……ct1)使用私钥d解密,计算出明文
RSA的理论基础:
欧几里得算法,中国剩余定理,Euler准则,Solovay-Strassen算法
RSA的安全性:1)共模攻击:两个用户的公钥中的模相同,虽然加密解密不同,但仍然是不安全的,可以通过扩展的欧几里得算法计算出来自重的明文,所以,公钥中每个实体的参数n不要相同。2)因子分解攻击:如果能够分解n得到p和q,Pollared p-1算法便可以得到Φ(n) = (p-1)(q-1)。
3.2 EIGamal公钥密码
ELGamal是一种较为常见的加密算法,基于1984年提出的公钥密码体制和椭圆曲线加密体系。ELGamal密码体制基于的困难问题是群中的离散对数问题。离散对数问题是在密码学中有着广泛应用的问题。ELGamal密码体制的构造方法可推广到一般的循环群中,如基于有限域和椭圆曲线的ELGamal面加密方案。ELGamal的特点是加密是概率的,即不同的明文加密后具有不同的密文。
ELGamal加密其实是利用DH密钥交换思想,产生随机密钥加密,然后传递生成随机密钥的“部件”,接收方利用该“部件”和自己的私钥生成随机密钥进行解密。ELGamal密码体制可以在任何离散对数问题难解的有限群中实现。
ElGamal公钥密码体制;设p是一个素数,使得(Z*p,*)上的离散对数问题是难处理的,令α∈Z*p是一个本原元,令p=Z*p,e=Z*p*Z*p,定义![]()
P,α,β是公钥,a是私钥。
对于K= (P,α,a,β),以及一个随机数K∈Zp-1,定义![]()
其中![]()
而![]()
对y1,y2∈Z*p,定义
![]()
ElGamal算法的理论基础:Shanks算法,Pollard p离散对数算法,Pohl,Hellman算法,z指数演算法,
ELGamal加密方案基于的安全问题 ELGamal加密方案的破解是指:给定(p,g,y=g4,c=m*yr),能够得出m。如果能破解,则可以c/m来得到yr,于是在给定gd, gr的情况下,得到了gdr,从而解决了DHP。另一方面,如果能够解决DHP,则可以在给定gd, gr的情况下,计算gdr,然后c/gdr来得到m,从而破解了DLP问题
基本的参数要求:前面提到加密不同消息必须使用不同的随机数r。假如同一个r加密两个消息m1,m2,结果为(c1,c3), (c2,c4)。由于c2/c4 = m1/m2。如果m1已知,则m2很容易计算出来。比特安全性,敌手能够观察到密文c = gr mod p和c3 = m*yr mod p。如果c是二次剩余。当且仅当r是偶数,因而敌手可以根据密文c来确定r的奇偶性。从公钥y = gd mod p是否是二次剩余,可以确定d的奇偶性。从而可以计算rd的奇偶性。于是可以确定y = gdrmod p是否是二次剩余。加上可以确定c3是否为二次剩余,于是从c3 = m*yr mod p可以确定m是否为二次剩余。因此,ELGamal加密泄露了m是否为二次剩余这一信息。因此不是语义安全的。即明文m是否为二次剩余这一比特信息不安全。 【2】
求解离散对数问题 与RSA问题中因子分解攻击方法类似,
ELGamal方案的破解的一个直接方法是求解离散对数问题。这是一种完全攻破,即给出公钥gd,可以求私钥d。
3.3 Rabin算法
大整数因子分解问题:给定一个正整数n,找到它的素因子分解,即将n写为,这里pi是不同的素数,且ei>1。
密钥的生成:机生成两个大的素数p和q,满足p=q=3mod4,计算n=p*q。n为公钥,q ,p,作为私钥。
加密算法:![]()
由于p=q=3mod4,可容易地算出c在模p下是2个方程根
![]()
和c在模q下的两个方程
![]()
两两组合联立,可以得到4个方程组:
求得4个m,其中必有一个m为明文。
Rabin密码体制的破解等价于大整数因子分解。由于大整数因子分解被公认是困难的,故Rabin密码体制不能破解。因此它是第一个可证明安全的个月密码体制。Rabin方案的可证明安全性:Rabin方案的攻破将会导致解决一个公认的困难问题。所谓“方案的攻破”,就是说给定Rabin方案密文,可得到明文。即拥有一个解密函数,给定y,返回y的4个平方根中的1个。
4. 总结
本文主要介绍了在信息安全发展过程之中的公钥密码体制的研究与发展,公钥加密现今已经被广泛的应用到如今的加密之中,并且较难破解,在金融与通信之中,较多的引用了ElGamal加密算法,公钥加密体制减少了对于密钥的传播的不安全性,使得加密变得简单,而只有拥有私钥的人才可以进行解密,使密码体制更加完善和简洁,公钥加密仍然在发展中,而且也有许多新的加密算法。
参考文献
[1] 密码学原理与实践(第三版)Douglas著
[2] 公钥密码体制研究与进展 陈晓峰
[3] 公钥加密体制的理论与实现论文