【学习图像处理】之实验二——灰度图像直方图规定化
灰度图像直方图规定化
-
- 图像增强
-
- 一、实验内容
- 二、灰度直方图
-
- 1、什么是灰度直方图?
- 2、直方图均衡化
- 3、直方图规定化
- 三、代码实现与分析
-
- 0、辅助功能实现
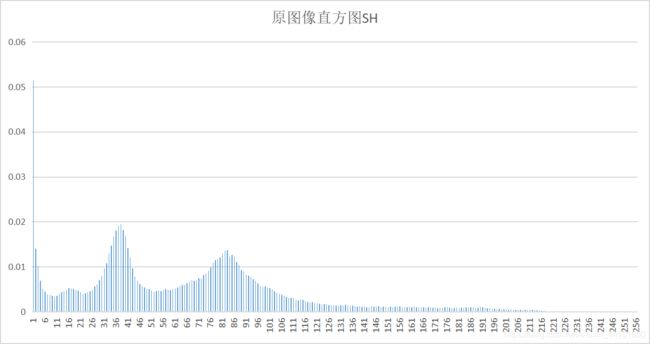
- 1、绘制原图像直方图SH
- 2、绘制均衡直方图SQH ,给出均衡图象QI
- 3、绘出目标均衡直方图EQH
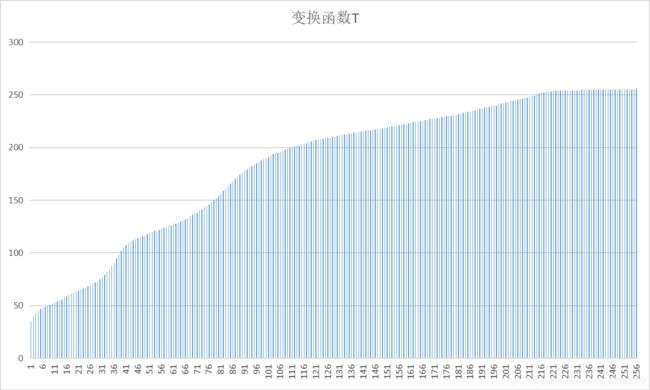
- 4、绘制规定化变换函数T,给出最终增强图象DI及其直方图DH
- 结语
图像增强
上一回我们通过进行图像反白、调整调色板取值和彩图变灰图的实验对bmp图像的数据格式有了比较熟练的了解。其实一张图片上往往只有很少一部分信息是我们真正需要的,而这些信息却埋没于茫茫的像素之中,利用起来很不方便,因此我们就需要对图像进行增强。
增强什么?当然是依据需求定向的加强指定内容。今天的主题就是对灰度图像进行直方图均衡化(Histogram Equalization)与直方图规定化(Histogram Specifications)处理。
一、实验内容
- 绘出原图象直方图SH
- 绘出直方图SH的均衡直方图SQH ,给出均衡图象QI
- 绘出目标直方图EH的均衡直方图EQH
- 绘出完成规定化任务的变换函数T,给出最终增强图象DI及其直方图DH
二、灰度直方图
1、什么是灰度直方图?
对于灰度图而言,画面是由很多个不同灰度值的像素组成的,图像中灰度的分布情况就成为了一个很重要的特征信息,因为它直接决定了整张图片什么信息最为突出,而另一些则不太明显。
灰度直方图,即是对图像中每个灰度级的像素数做了统计,绘制成的以灰度级为横坐标,像素个数(频率)为纵坐标的图像,它能够直观的体现灰度图像中某种灰度出现的概率,表达式为: P r ( r k ) = n k n Pr(rk)=\frac{nk}{n} Pr(rk)=nnk ,其中 r k rk rk为灰阶, n k nk nk表示灰度级为 r k rk rk的像元数目。
当然直方图也有一个很明显的缺点,就是它丢失了像素所在位置的信息。
2、直方图均衡化
一般一张自然的灰度图都会集中在相对较窄的一段灰阶内,这样就会导致细节丢失。如果我们通过某种手段,把灰度区间拉大或者让灰度尽可能均匀分布,这样做就可以增大图像对比度,从而把细节信息显示出来。
直方图均衡化就是一种达成上述目的的手段。均衡化处理后,灰度范围变大,对比度变大,清晰度变大,能够有效增强图像。其具体的推导过程涉及概率论中知识,感兴趣可以看这位作者撰写的直方图均衡化的数学原理,而它的作用解释可以见直方图均衡化作用。
对于我们写代码而言,只需要知道最终的变换公式即可:
y = f ( x ) = ( L − 1 ) ∑ 0 x i h ( x i ) w ∗ h y=f(x)=(L-1)\sum_{0}^{x_i} \frac{h(x_i)}{w*h} y=f(x)=(L−1)∑0xiw∗hh(xi)
3、直方图规定化
上面讲到了直方图均衡化,现在有一个问题:如果两张图片s和u,他们都可以均衡化到t,那是否意味着s可以通过某种方法转换成u呢?答案是肯定的,我们用几个公式来表示s、u、t间的关系:
t = T ( s k ) = ∑ i = 0 k p s ( s i ) t=T(s_k)=\sum_{i=0}^{k} p_s(s_i) t=T(sk)=∑i=0kps(si) (1) k = 0 , 1 , . . . , M − 1 k=0,1,...,M-1 k=0,1,...,M−1
t = T u ( u j ) = ∑ j = 0 l p u ( u j ) t=T_u(u_j)=\sum_{j=0}^{l} p_u(u_j) t=Tu(uj)=∑j=0lpu(uj) (2) l = 0 , 1 , . . . , N − 1 l=0,1,...,N-1 l=0,1,...,N−1
由此可见,我们想要通过均衡化的结果逆求出u是可行的。我们只需要找到s到u的映射关系T,而这个关系应该是:
∣ ∑ i = 0 k p s ( s i ) − ∑ i = 0 l p u ( u j ) ∣ |\sum_{i=0}^{k} p_s(s_i)-\sum_{i=0}^{l} p_u(u_j)| ∣∑i=0kps(si)−∑i=0lpu(uj)∣
三、代码实现与分析
这次实验中我们用下面这张图作为原图像:
0、辅助功能实现
如果你仔细分析一下实验的每一步,会发现我们需要多次的存储用以绘制直方图的数据,而且这个数据往往是保存在一个数组之中,因此我们可以专门写一个函数将数组保存到txt文件中去。
template<typename T>
bool array2txt(T &H,const char* cFilename) //将一个数组输出到以cFilename命名的txt文件中
{
ofstream outfile;
outfile.open(cFilename, ios::out);
if (!outfile.is_open())
{
cout << "Open file failure" << endl;
return false;
}
for (int i = 0; i < (sizeof(H)/sizeof(H[0])); i++) //遍历数组写入txt
{
outfile << H[i] << "\t" ;
}
return true;
}
可以看到,这里我为了能够反复利用使用了模版函数和c++中的文件流输出语句,以此来避免文件输出时该用%d还是%f的问题。不过实际上我们大部分数据都是float类型的数组,所以模版函数是可选的。
1、绘制原图像直方图SH
正式开始实验,在本次实验中的直方图我都以“灰阶-概率”的形式输出,如果你想输出“灰阶-频率”的直方图,那么不要除以总数即可。
float* outHistogramData(BMPFILE &src,const char*cFilename)//将绘制“灰阶-概率”直方图的数据保存到txt文件中
{
float H[256] = {
0 }; //8bit的灰度图,256灰阶
int i, j;
float *result = (float*)malloc(256 * sizeof(float));
int total = src.imageh * src.imagew;
for (i = 0; i < src.imageh; i++)
for (j = 0; j < src.imagew; j++)
{
H[src.pDataAt(i)[j]] += 1.0; //对每个灰阶进行计数
}
for (i = 0; i < 256; i++)
{
H[i] /= (float)total; //计算图像概率p(Sk)
result[i] = H[i];
}
if (!array2txt(H,cFilename))
{
printf("outHistogramData error!\n");
exit(0);
}
return result;
}
这里一定要注意,如果你想要返回函数中新建的一个数组,那么一定要用malloc对它进行内存分配,否则返回后的指针将是野指针。同时,由于我array2txt函数的定义问题,它不可以接受一个指针表示的数组,这个可以由你自行修改。我的解决办法是单独创建一个定长数组H[256],让它传入array2txt函数,另分配一个指针result返回结果。
我们得到的txt文本中数据大致长这个样子(后面的过程我就不贴数据的图了)

把这些数据导入到Excel表格中即可做出我们要的直方图SH:
2、绘制均衡直方图SQH ,给出均衡图象QI
根据我们之前的分析,均衡直方图的求解需要对“灰阶-概率”数据进行累加处理,然后再扩展到8bit对应的0-255范围上。这里“灰阶-概率”我们可以利用上一步中得到的数据(当然你也可以再算一遍,少传一个参数)
float* HistEqualize(BMPFILE &src,BMPFILE &des,float* hist_data, const char*cFilename) //已知灰阶-概率矩阵,做直方图均衡化
{
float count_origin[256] = {
0 }, T[256] = {
0 }, count_new[256] = {
0 };
//count_origin用来记录原图像各灰阶个数,count_new是均衡化之后的结果
float *result = (float*)malloc(256 * sizeof(float)); //返回均衡化后的灰阶-概率矩阵
int i, j;
int total = src.imageh * src.imagew;
for (i = 0; i < 256; i++)
{
count_origin[i] = hist_data[i] * total; //求原图中的灰阶计数
}
for (i = 0; i < 256; i++)
for (j = 0; j <= i; j++)
{
T[i] += hist_data[j]; //求得均衡化之后的tk
result[i] = T[i]; //如果需要作图的那么result=count_new,如果需要均衡化result=T
}
if(!array2txt(T, "tk_data.txt"))
{
printf("outHistogramData error!\n");
exit(0);
}
for (i = 0; i < 256; i++)
{
T[i] = int((256 - 1)*T[i] + 0.5); //用式tk=int((L-1)*tk+0.5)将tk扩展至[0,L-1]范围,得到灰度级
}
for (i = 0; i < src.imageh; i++)
for (j = 0; j < src.imagew; j++)
{
des.pDataAt(i)[j] = T[src.pDataAt(i)[j]]; //将新的值赋予给输出图像
}
for (i = 0; i < 256; i++)
{
count_new[int(T[i])] += count_origin[i]; //根据新的灰度级求新的计数
}
for (i = 0; i < 256; i++)
{
count_new[i] /= (float)total; //计算新图像概率p(tk)
//result[i] = count_new[i]; //如果需要作图的那么result=count_new,如果需要均衡化result=T
}
if(!array2txt(count_new, cFilename))
{
printf("outHistogramData error!\n");
exit(0);
}
des.SaveBMPFILE("QI.bmp");
return result;
}
对于最后输出图像的赋值以及灰阶的重新计数如果有不明白的,可以看看下面这张图:
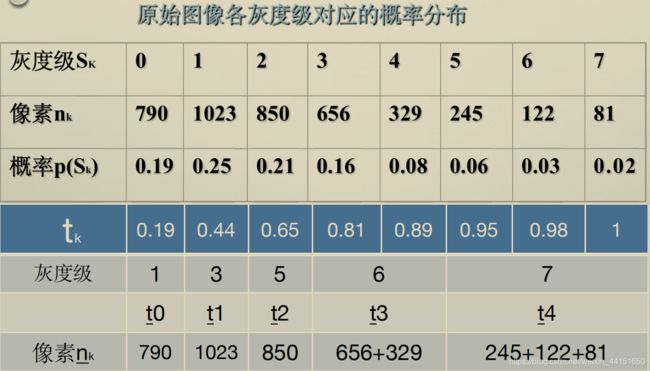
我举一个例子,如果原图中灰度级为3,那么它在输出图像中的灰度级就应该是T[3]=6。这就是为什么
des.pDataAt(i)[j] = T[src.pDataAt(i)[j]];
count_new[int(T[i])] += count_origin[i];
//count_new初值为0
3、绘出目标均衡直方图EQH
可能是直接给出直方图数据缺乏挑战性,老师给了我们一个函数,要求将函数转换为目标直方图。函数表达式为:
y = a ( 1 4 ( x − 1 2 ) 2 ) y=a(\frac{1}{4}(x-\frac{1}{2})^{2}) y=a(41(x−21)2), x ∈ [ 0 , 1 ] x\in[0,1] x∈[0,1]
注意到函数中含有未知量a,所以我们需要找到方程解出a的值。既然它代表直方图,那么它就应该符合直方图的性质——频率之和为1。有了这个入手点,我们就可以列方程了:
1 = ∫ 0 1 f ( x ) d x 1=\int_{0}^{1} f(x)dx 1=∫01f(x)dx
接下来通过微分的基本思想,求解未知数:
float calculateA() //计算 y=a(1/4-(x-1/2)^2)中的a
{
//一种比较直观且简单的算法是分割成多份然后求面积和,最后用1/sum即可求得a(因为概率和应为1)
int i;
float x[1000]; //定义域[0,1]分割成0.001为步长的1000份
float y[1000]; //值域
float sum = 0;
for (i = 0; i < 1000; i++) //由于c语言只能用整数下标,因此只能将x取值存为数组
{
x[i] = i * 0.001;
}
for (i = 0; i < 1000; i++) //计算x对应的y值
{
y[i] = (0.25 - pow((x[i] - 0.5), 2)); //y=(1/4-(x-1/2)^2)
}
for (int i = 0; i < 1000; i++) //计算面积和
{
sum += y[i] * 0.001;
}
return (1 / sum);
}
求得a的值无限逼近于6,因此函数即为 y = 6 ( 1 4 ( x − 1 2 ) 2 ) y=6(\frac{1}{4}(x-\frac{1}{2})^{2}) y=6(41(x−21)2)。接下来我们需要把图像放缩到0-255的区间上,可以仿照上面的微分思路,将0-1均分为256份,然后分别求概率值即可(注意结果也要相应放缩)。
这样我们就得到了目标直方图EH的“灰阶-概率”数据,将其传入2中函数(这里理论上是无法得出图像的,但是因为u也是s经过某种处理后得到的图像,因此我们可以将s作为原图传入函数中),即可求得EQH:
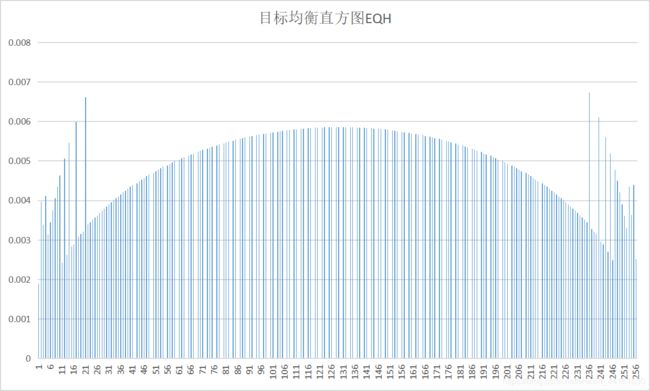
4、绘制规定化变换函数T,给出最终增强图象DI及其直方图DH
在完成步骤2、3的过程中我们已经求得了SQH_tk和EQH_tk两个数组,即直方图规定化所需要的所有数据已经齐了,接下来我们按照公式去求规定化需要的映射函数T。规定化的主要步骤就是把SQH_tk中的每一个灰度映射到一个EQH_tk中与之差值最小的灰度值上,由于tk是单调递增的,因此我们只需要判断到第一个大于SQH_tk[i]的值即可。得到映射函数T之后,我们将原图像中的像素按照映射关系重新赋值即可得到DI。代码如下:
int* HistSpecificate(HXLBMPFILE &src, HXLBMPFILE &des, float* hist_data, const char*cFilename) //直方图规定化
{
int i, j, index=0;
float *SQH_tk = HistEqualize(src, des, "SQH.txt"); //获取原图像的均衡化tk数组
float *EQH_tk = HistEqualize(src, des, hist_data,"EQH.txt"); //获取目标图像的均衡化tk数组
int T[256]; //灰阶对应关系矩阵
int *result = (int*)malloc(256 * sizeof(int));
float min, temp;
for (i = 0; i < 256; i++)
{
min = fabs(SQH_tk[i] - EQH_tk[0]); //假设最小值
for (j = index; j < 256; j++)
{
temp = fabs(SQH_tk[i] - EQH_tk[j]); //依次做差找到最小值
if (temp < min)
{
min = temp;
index=j;
}
if (SQH_tk[i] < EQH_tk[j])
break;
}
T[i] = index; //保存映射结果
result[i] = index;
}
if(!array2txt(T,"HistSpecificate.txt"))
{
printf("outHistogramData error!\n");
exit(0);
}
for (i = 0; i < src.imageh; i++)
for (j = 0; j < src.imagew; j++)
{
des.pDataAt(i)[j] = T[src.pDataAt(i)[j]]; //将新的值赋予给输出图像
}
des.SaveBMPFILE("DI.bmp");
outHistogramData(des, cFilename);
return result;
}
最终得到的变换函数T如图:
结语
第二次图像处理的实验,说实话直方图均衡化的代码写起来很简单,但是真正的重点在于如何理解直方图均衡化以及规定化的意义,因为实际应用中我们可以直接从opencv这样的库中调用函数。况且如果是为了写代码而写,那么完全可以去一些OJ网站刷题,因此对于算法的理解才是学习过程中应该注意的地方。
本次实验完整的项目文件与代码可见我的gitee。