时序分析 20 高斯混合模型 (上)
时序分析 20 高斯混合模型 (上)
前言
在时序分析中,我们经常需要对时序数据进行分段(Time Series Segmentaion),对于金融时序数据尤其如此。我们多次观察到某个时序数据在不同的时间阶段展现除了不同的统计特征和特性,也就是说该时序是不平稳的。通常在这种情况下,我们需要采用诸如GARCH,差分等技术对该时序数据进行建模,但是如果我们可以把整个时序分成几个阶段,而在一个阶段内其统计特性或者某些特征接近,从而对于各个阶段结合业务特征和属性分别建模,很可能可以得到更好的结果。
注: 前面讨论过的隐含马尔可夫模型(HMM)实际上就是可以达到这个目的的一种模型技术。
这次我们要讨论的是与HMM有异曲同工之妙的另外一种方法: 高斯混合模型 (Gaussian Mixed Model, GMM)。
如前面我们描述的那样,时序分段似乎可以理解为对时序数据进行聚类(Time Series Clustering)。基于这种直观理解,我们首先要讨论与高斯混合模型有非常密切关系的Kmean聚类算法,然后再详细分析高斯混合模型的特点和不同之处。
聚类算法回顾
首先,让我们简单回归一下Kmeans聚类算法。(关于Kmeans聚类算法的具体细节,请读者查阅相关文档或者是本人的机器学习讲义中关于Kmeans算法的描述)
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
# Generate some data
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4,
cluster_std=0.60, random_state=0)
X = X[:, ::-1] # flip axes for better plotting
# Plot the data with K Means Labels
from sklearn.cluster import KMeans
kmeans = KMeans(4, random_state=0)
labels = kmeans.fit(X).predict(X)
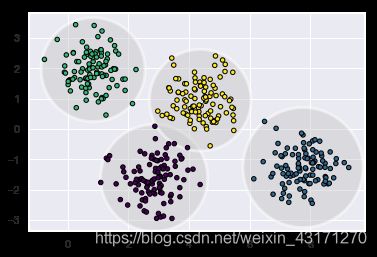
plt.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis',edgecolor='black');

直观上,聚类算法在把某个点分配到某个聚类上时,它应该能够给出这个分配的不确定性。因为有些点的分配可能很确定,而可能有些点的分配不是很确定。例如位于两个聚类的交界边缘的点到底应该分配到哪一个类就不是很确定,反之临近聚类中心的点就比较确定。但是Kmeans算法并没有给出这种不确定性的度量。
一种思考Kmeans模型的思路是以聚类中心点为圆心画一个圆,圆的半径指定了属于这个聚类的最远距离。让我们来看一下,
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
def plot_kmeans(kmeans, X, n_clusters=4, rseed=0, ax=None):
labels = kmeans.fit_predict(X)
# plot the input data
ax = ax or plt.gca()
ax.axis('equal')
ax.scatter(X[:, 0], X[:, 1], c=labels, s=20, cmap='viridis', zorder=2,edgecolor='black')
# plot the representation of the KMeans model
centers = kmeans.cluster_centers_
radii = [cdist(X[labels == i], [center]).max()
for i, center in enumerate(centers)]
for c, r in zip(centers, radii):
ax.add_patch(plt.Circle(c, r, fc='#CCCCCC', lw=3, alpha=0.5, zorder=1))
kmeans = KMeans(n_clusters=4, random_state=0)
plot_kmeans(kmeans, X)
所以,Kmeans算法假设同一聚类下的点是以圆形来分布在聚类中心的,如果是其他形状,Kmeans算法将不能很好的解决。我们可以通过转换数据的坐标来演示这一点。
rng = np.random.RandomState(13)
X_stretched = np.dot(X, rng.randn(2, 2))
kmeans = KMeans(n_clusters=4, random_state=0)
plot_kmeans(kmeans, X_stretched)

从上图可以观察到,由于数据不再是圆形分布聚类,Kmeans算法已经不能很好地拟合这一点。
有的时候,分析人员可以通过PCA来修正这一点,但PCA并不能保证适用于所有地情况。
到这里,我们得到了Kmeans算法的两个缺点:
- 不能给出分配到聚类的不确定性
- 对于非圆形分布的聚类不能很好的拟合
高斯混合模型
高斯混合模型尝试去找到多维混合高斯概率分布能够最好地拟合数据。它不仅可以适合于分类问题,也可以使用于回归问题。本系列文章前面所讨论的VAR(Vector AutoRegression)就可以被看成是高斯混合模型在回归问题上的一种特殊应用。
from sklearn import mixture
gmm = mixture.GaussianMixture(n_components=4,covariance_type='full').fit(X)
labels = gmm.predict(X)
plt.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis',edgecolor='black');

从上图我们可以看出,高斯混合模型可以非常容易地实现Kmeans算法的效果,实际上Kmeans算法也就是高斯混合模型的一个应用。
另外,GMM可以给出数据点分配给某个聚类的概率意义上的确定性。
probs = gmm.predict_proba(X)
print(probs[:5].round(3))
[[0. 0.531 0.469 0. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 1. 0. 0. ]
[0. 0. 0. 1. ]]
我们也可以可视化这一点
size = 50 * probs.max(1) ** 2 # square emphasizes differences
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=size,edgecolor='black');
GMM采用EM(Expectation Maximum)-期望最大化算法来求解,主要过程分为两步,
- 随机选择每个聚类的分布的位置和形状。
- 应用EM算法直到收敛
E-step: 对于每一个点,找到其分配到各个聚类的概率的期望值。
M-step: 对于每一个聚类,使用E-step的结果来更新其分布从而使期望值最大。
初始分布的选择对于GMM的结果有比较重要的影响,有的时候GMM收敛的结果并不是全局最优解,所以在实践中我们进场会多选几次初始分布然后比较结果从而得到最优解。
from matplotlib.patches import Ellipse
def draw_ellipse(position, covariance, ax=None, **kwargs):
"""Draw an ellipse with a given position and covariance"""
ax = ax or plt.gca()
# Convert covariance to principal axes
if covariance.shape == (2, 2):
U, s, Vt = np.linalg.svd(covariance)
angle = np.degrees(np.arctan2(U[1, 0], U[0, 0]))
width, height = 2 * np.sqrt(s)
else:
angle = 0
width, height = 2 * np.sqrt(covariance)
# Draw the Ellipse
for nsig in range(1, 4):
ax.add_patch(Ellipse(position, nsig * width, nsig * height,
angle, **kwargs))
def plot_gmm(gmm, X, label=True, ax=None):
ax = ax or plt.gca()
labels = gmm.fit(X).predict(X)
if label:
ax.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis', zorder=2,edgecolor='black')
else:
ax.scatter(X[:, 0], X[:, 1], s=40, zorder=2)
ax.axis('equal')
w_factor = 0.2 / gmm.weights_.max()
for pos, covar, w in zip(gmm.means_, gmm.covariances_, gmm.weights_):
draw_ellipse(pos, covar, alpha=w * w_factor)
gmm = mixture.GaussianMixture(n_components=4).fit(X)
plot_gmm(gmm, X)
gmm = mixture.GaussianMixture(n_components=4, covariance_type='full', random_state=42)
plot_gmm(gmm, X_stretched)

显而易见,用GMM来拟合非圆形分布聚类效果要优于Kmeans.
GMM不仅可以进行聚类,还可以用来做密度函数估计等多种用途。本文只是简要介绍GMM的基本作用和工作原理,详细信息请读者参阅相关文档或本人的其他系列文章(机器学习讲义).
关于聚类个数的选择,可以根据AIC/BIC准则结合业务特征属性来决定。
本文的下半部分将集中讨论GMM在时序分段(Time Series Segmentation)方面的应用。
未完,待续…

