深度学习 (十一)：实战KAGGLE房价预测数据 (附带数据集)

引入

  本文主要对KAGGLE房价预测数据进行预测，并提供模型的设计以及超参数的选择${}^{[1]}$。
  数据集介绍可参照：
  https://blog.csdn.net/weixin_44575152/article/details/110852303
  已处理数据可参照：
  https://gitee.com/inkiinki/data20201205/blob/master/Data20201205/kaggle_house_price.rar

1 库引入

import torch
import torch.nn as nn
import torch.utils.data as data
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
torch.set_default_tensor_type(torch.FloatTensor)

2 数据载入

def load_data(tr_path='../Data/house_price_train.csv', te_path='../Data/house_price_test.csv'):
    """
    Load data.
    """
    ret_tr_data = pd.read_csv(tr_path).values
    ret_te_data = pd.read_csv(te_path).values
    ret_tr_label = np.reshape(ret_tr_data[:, -1], (len(ret_tr_data), 1))

    return (torch.tensor(ret_tr_data[:, :-1], dtype=torch.float),
            torch.tensor(ret_tr_label, dtype=torch.float),
            torch.tensor(ret_te_data, dtype=torch.float))

3 获取网络

  本文使用基本的线性回归模型来训练模型：

def get_net(num_features):
    """
    Generate the net.
    """
    ret_net = nn.Linear(num_features, 1)
    for param in ret_net.parameters():
        nn.init.normal_(param, mean=0, std=0.01)
    return ret_net

4 评价函数

  使用对数均方根误差函数作为模型评价函数：
$$\sqrt{\frac{1}{n}\sum _{i=1}^n(\log (y_i)-\log (\widehat{y_i}){)}^2}\text{\hspace{1em}(1)}$$其中$\widehat{y_i}$是预测值，$y_i$是真是标签。
  实现如下：

def log_rmse(net, x, y, loss=nn.MSELoss()):
    """
    The log root-mean-square error
    """
    with torch.no_grad():
        # Set the value (< 1) to 1.
        # The result will be more stable.
        temp_predicted = torch.max(net(x), torch.tensor(1.0))
        ret_rmse = torch.sqrt(2 * loss(torch.log(temp_predicted), torch.log(y)).mean())
    return ret_rmse.item()

5 训练函数

  与丢弃法中使用SGD优化算法不同，这里使用Adam优化算法：相比SGD，它对学习率相对不敏感。

def train(net, tr_data, tr_label, te_data, te_label,
          num_epochs=100, lr=5, weight_decay=0, batch_size=64, loss=nn.MSELoss()):
    """
    The train function by using adam optimization algorithms, and its not sensitive to learning rate.
    """
    ret_tr_loss, ret_te_loss = [], []
    # Get the train iterator.
    temp_tr_data_iter = data.TensorDataset(tr_data, tr_label)
    temp_tr_data_iter = data.DataLoader(temp_tr_data_iter, batch_size, shuffle=True)
    temp_optimizer = torch.optim.Adam(params=net.parameters(), lr=lr, weight_decay=weight_decay)
    net = net.float()
    for idx_epoch in range(num_epochs):
        for x, y in temp_tr_data_iter:
            temp_loss = loss(net(x.float()), y.float())
            temp_optimizer.zero_grad()
            temp_loss.backward()
            temp_optimizer.step()
        ret_tr_loss.append(log_rmse(net, tr_data, tr_label))
        if te_label is not None:
            ret_te_loss.append(log_rmse(net, te_data, te_label))

    return ret_tr_loss, ret_te_loss

6 $k$折交叉验证

  使用以下代码或者$k$折交叉验证的第$i$折的数据：

def get_k_fold_data(k, i, x, y):
    """
    Get the training data and test data of i-th k-th cross validation.
    """
    assert k > 1
    temp_num_fold = x.shape[0] // k
    temp_start_idx = i * temp_num_fold
    temp_end_idx = (i + 1) * temp_num_fold
    # The test set.
    ret_x_te, ret_y_te = x[temp_start_idx: temp_end_idx, :], y[temp_start_idx: temp_end_idx]
    # The training set.
    temp_idx = list(range(0, temp_start_idx)) + list(range(temp_end_idx, x.shape[0]))
    ret_x_tr, ret_y_tr = x[temp_idx, :], y[temp_idx]

    return ret_x_tr, ret_y_tr, ret_x_te, ret_y_te

7 主函数

  绘图函数与多项式拟合实验一致。

def main(tr_data, tr_label, k=10, num_epochs=100, lr=5, weight_decay=0, batch_size=64):
    """
    The main function: k-th cross validation experiments.
    """

    # Get loss.
    temp_loss = nn.MSELoss()

    # The main loops.
    ret_tr_loss_sum, ret_va_loss_sum = 0, 0
    for i in range(k):
        temp_data = get_k_fold_data(k, i, tr_data, tr_label)
        temp_net = get_net(tr_data.shape[1])
        temp_tr_loss, temp_te_loss = train(temp_net, *temp_data, num_epochs, lr, weight_decay, batch_size)
        ret_tr_loss_sum += temp_tr_loss[-1]
        ret_va_loss_sum += temp_te_loss[-1]
        if i == 0:
            plot(range(1, num_epochs + 1), temp_tr_loss, 'epochs', 'rmse',
                 range(1, num_epochs + 1), temp_te_loss, ['training', 'valid'])
        print("Fold %d, training rmse %.6f, valid rmse %.6f" % (i, temp_tr_loss[-1], temp_te_loss[-1]))

    ret_tr_loss_sum /= k
    ret_va_loss_sum /= k
    print("The ave training rmse %.6f, valid rmse %.6f" % (ret_tr_loss_sum, ret_va_loss_sum))
    return ret_tr_loss_sum, ret_va_loss_sum


if __name__ == '__main__':
    # Parameters setting.
    # Load datasets, including training data, training data label and test label.
    temp_tr_data, temp_tr_label, temp_te_data = load_data()
    main(temp_tr_data, temp_tr_label, num_epochs=50)

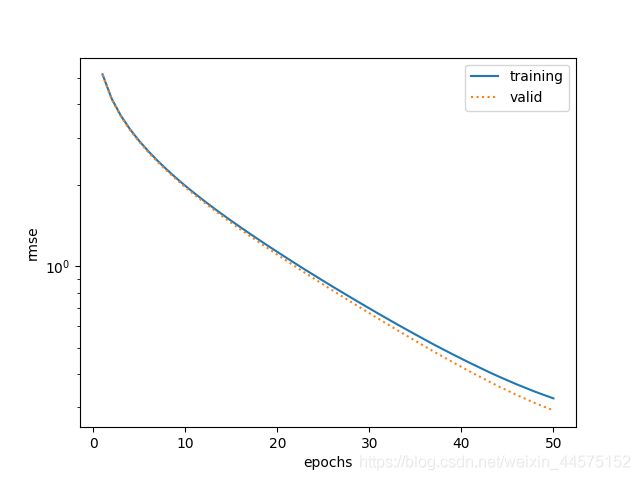
  运行结果如下：

Fold 0, training rmse 0.324291, valid rmse 0.292623
Fold 1, training rmse 0.324346, valid rmse 0.343651
Fold 2, training rmse 0.323409, valid rmse 0.327304
Fold 3, training rmse 0.320075, valid rmse 0.359999
Fold 4, training rmse 0.321923, valid rmse 0.370078
Fold 5, training rmse 0.324752, valid rmse 0.304950
Fold 6, training rmse 0.324033, valid rmse 0.293289
Fold 7, training rmse 0.324214, valid rmse 0.306041
Fold 8, training rmse 0.318781, valid rmse 0.364510
Fold 9, training rmse 0.325100, valid rmse 0.293933
The ave training rmse 0.323092, valid rmse 0.325638

  损失变化如下：

完整代码

import torch
import torch.nn as nn
import torch.utils.data as data
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
torch.set_default_tensor_type(torch.FloatTensor)


def load_data(tr_path='../Data/house_price_train.csv', te_path='../Data/house_price_test.csv'):
    """
    Load data.
    """
    ret_tr_data = pd.read_csv(tr_path).values
    ret_te_data = pd.read_csv(te_path).values
    ret_tr_label = np.reshape(ret_tr_data[:, -1], (len(ret_tr_data), 1))

    return (torch.tensor(ret_tr_data[:, :-1], dtype=torch.float),
            torch.tensor(ret_tr_label, dtype=torch.float),
            torch.tensor(ret_te_data, dtype=torch.float))


def get_net(num_features):
    """
    Generate the net.
    """
    ret_net = nn.Linear(num_features, 1)
    for param in ret_net.parameters():
        nn.init.normal_(param, mean=0, std=0.01)
    return ret_net


def log_rmse(net, x, y, loss=nn.MSELoss()):
    """
    The log root-mean-square error
    """
    with torch.no_grad():
        # Set the value (< 1) to 1.
        # The result will be more stable.
        temp_predicted = torch.max(net(x), torch.tensor(1.0))
        ret_rmse = torch.sqrt(2 * loss(torch.log(temp_predicted), torch.log(y)).mean())
    return ret_rmse.item()


def train(net, tr_data, tr_label, te_data, te_label,
          num_epochs=100, lr=5, weight_decay=0, batch_size=64, loss=nn.MSELoss()):
    """
    The train function by using adam optimization algorithms, and its not sensitive to learning rate.
    """
    ret_tr_loss, ret_te_loss = [], []
    # Get the train iterator.
    temp_tr_data_iter = data.TensorDataset(tr_data, tr_label)
    temp_tr_data_iter = data.DataLoader(temp_tr_data_iter, batch_size, shuffle=True)
    temp_optimizer = torch.optim.Adam(params=net.parameters(), lr=lr, weight_decay=weight_decay)
    net = net.float()
    for idx_epoch in range(num_epochs):
        for x, y in temp_tr_data_iter:
            temp_loss = loss(net(x.float()), y.float())
            temp_optimizer.zero_grad()
            temp_loss.backward()
            temp_optimizer.step()
        ret_tr_loss.append(log_rmse(net, tr_data, tr_label))
        if te_label is not None:
            ret_te_loss.append(log_rmse(net, te_data, te_label))

    return ret_tr_loss, ret_te_loss


def get_k_fold_data(k, i, x, y):
    """
    Get the training data and test data of i-th k-th cross validation.
    """
    assert k > 1
    temp_num_fold = x.shape[0] // k
    temp_start_idx = i * temp_num_fold
    temp_end_idx = (i + 1) * temp_num_fold
    # The test set.
    ret_x_te, ret_y_te = x[temp_start_idx: temp_end_idx, :], y[temp_start_idx: temp_end_idx]
    # The training set.
    temp_idx = list(range(0, temp_start_idx)) + list(range(temp_end_idx, x.shape[0]))
    ret_x_tr, ret_y_tr = x[temp_idx, :], y[temp_idx]

    return ret_x_tr, ret_y_tr, ret_x_te, ret_y_te


def plot(x, y, x_label, y_label, x1=None, y1=None, legend=None):
    """
    The plot function.
    """
    plt.semilogy(x, y)
    plt.xlabel(x_label)
    plt.ylabel(y_label)

    if x1 and y1:
        plt.semilogy(x1, y1, linestyle=':')
        plt.legend(legend)
    plt.show()
    plt.close()


def main(tr_data, tr_label, te_data, k=10, num_epochs=100, lr=5, weight_decay=0, batch_size=64):
    """
    The main function: k-th cross validation experiments.
    """

    # Get loss.
    temp_loss = nn.MSELoss()

    # The main loops.
    ret_tr_loss_sum, ret_va_loss_sum = 0, 0
    for i in range(k):
        temp_data = get_k_fold_data(k, i, tr_data, tr_label)
        temp_net = get_net(tr_data.shape[1])
        temp_tr_loss, temp_te_loss = train(temp_net, *temp_data, num_epochs, lr, weight_decay, batch_size)
        ret_tr_loss_sum += temp_tr_loss[-1]
        ret_va_loss_sum += temp_te_loss[-1]
        # temp_predicted = temp_net(te_data)

        if i == 0:
            plot(range(1, num_epochs + 1), temp_tr_loss, 'epochs', 'rmse',
                 range(1, num_epochs + 1), temp_te_loss, ['training', 'valid'])
        print("Fold %d, training rmse %.6f, valid rmse %.6f" % (i, temp_tr_loss[-1], temp_te_loss[-1]))

    ret_tr_loss_sum /= k
    ret_va_loss_sum /= k
    print("The ave training rmse %.6f, valid rmse %.6f" % (ret_tr_loss_sum, ret_va_loss_sum))
    return ret_tr_loss_sum, ret_va_loss_sum


if __name__ == '__main__':
    # Parameters setting.
    # Load datasets, including training data, training data label and test label.
    temp_tr_data, temp_tr_label, temp_te_data = load_data()
    main(temp_tr_data, temp_tr_label, temp_te_data, num_epochs=50)

---

参考文献
[1] 李沐、Aston Zhang等老师的这本《动手学深度学习》一书。