红黑树为一棵二叉搜索树,它为每个结点增加一个变量存储结点颜色,利用结点颜色对树的形状进行约束,使其近似平衡(并非完全平衡)。
红黑树有五个性质:
1. 每个结点为红色或者黑色。
2. 根结点为黑色。
3. 每个叶结点为黑色(NIL)。
4. 如果一个结点为红色,则其子结点均为黑色。
5. 对每个结点,从该结点到其所有后代的叶结点的简单路径均包含相同数目的黑色结点。
红黑树有五个基本属性:color、key、left、right、parent,分别为颜色,关键字,左树,右树,双亲。
在红黑树中,用一个哨兵结点 T.NIL来处理边界条件,其color设为BLACK,其它值任意,所有指向NULL的指针都用哨兵替换。
接下来对红黑树操作的过程做一些解释(代码采用C\C++)。
//红黑树的三叉链表存储结构
typedef short Other;
typedef struct{
string Color;
Other Info;
int key;
}TreeData;
typedef struct RBTNode{
TreeData data;
struct RBTNode *left, *right, *parent;
}RBTNode, *RBTree;
基本操作功能:
void CreatBSTree(RBTree &); //建立红黑树
void InsertTree(RBTree &, TreeData); //插入数据(允许数据重复)
void RBInsertFixUp(RBTree &, RBTree); //插入数据后维护工作
void Transplant(RBTree &, RBTree, RBTree); //移动子树
void LeftRotate(RBTree &, RBTree); //左旋
void RightRotate(RBTree &, RBTree); //右旋
int Delete(RBTree &, int); //删除数据结点
void RBDeleteFixUp(RBTree &, RBTree); //删除数据后维护工作
RBTree Minimum(RBTree); //找最小值
RBTree Maximum(RBTree); //找最大值
RBTree Search(RBTree, int); //搜索结点
RBTree Successor(RBTree); //寻找后继
RBTree Predecessor(RBTree); //寻找前驱
void InOrderTraverse(RBTree); //中序遍历树(由小到大排列输出)
void PostOrderTraverse(RBTree); //后序遍历
void test(RBTree); //测试功能
RBTree Nil = new RBTNode; //哨兵结点
Nil->left = Nil->right = Nil->parent = NULL;
Nil->data.key = 0x3f3f3f3f; //设置无穷大
Nil->data.Color = BLACK;
RBTree T; //实例化一棵树,并设其初值指向Nil
T = Nil;
T->parent = Nil;
--------------------初始化工作完成-----------------
//中序遍历树(由小到大排列输出)
void InOrderTraverse(RBTree T){
if (T != Nil){
InOrderTraverse(T->left); //左树
cout << "(" << T->data.key << "," << T->data.Color << ")->";//根结点
InOrderTraverse(T->right); //右树
}
}
//后序遍历
void PostOrderTraverse(RBTree T){
if (T != Nil){
PostOrderTraverse(T->left); //左树
PostOrderTraverse(T->right); //右树
cout << "(" << T->data.key << "," << T->data.Color << ")->";//根结点
}
}
树的遍历方法,通过递归调用函数,并在不同时间访问即可得到相应的遍历顺序,通过中序加一个先序或后续可以确定一棵树。
接下来的左旋、找最小值、寻找后继,与右旋,最大值,找前驱对称
//左旋
void LeftRotate(RBTree &T, RBTree x){
RBTree y;
y = x->right;
x->right = y->left;
if (y->left != Nil)
y->left->parent = x;
y->parent = x->parent;
if (x->parent == Nil)
T = y;
else if (x == x->parent->left)
x->parent->left = y;
else
x->parent->right = y;
y->left = x;
x->parent = y;
}
旋转能够保持搜索二叉树性质的局部操作,它使y成为该子树新的根结点,x成为y的左树,y成为x的右孩。
--------------------------------------------------------------------
//找最小值,一定在最左边
RBTree Minimum(RBTree T){
while (T->left != Nil)
T = T->left;
return T;
}
//寻找后继,右树的最小值即为后继
RBTree Successor(RBTree T){
if (T->right != Nil)
return Minimum(T->right);
RBTree X = T->parent;
while (X != Nil&&T == X->right) {
T = X;
X = X->parent;
}
return X;
}
//搜索结点
RBTree Search(RBTree T, int e){
while (T != Nil&&e != T->data.key){
if (e < T->data.key)
T = T->left;
else
T = T->right;
}
return T;
}
------------------------------------------------------------------------
插入和删除操作是比较复杂的一个操作,因为其可能破坏红黑树的性质,需要对其进行维护。
插入数据时像二叉搜索树一样,先找出插入的位置,然后把插入结点置为红色,再调用插入维护过程,维护红黑树性质。插入操作主要破坏了性质6.如果一个结点为红色,则其子结点均为黑色。性质2. 根结点为黑色。
//插入数据(允许数据重复)
void InsertTree(RBTree &T, TreeData e){
RBTree z = new RBTNode;
z->data = e;
RBTree y = Nil;
RBTree x = T;
while (x != Nil){
y = x; //记录父结点
if (z->data.key <= x->data.key)
x = x->left;
else x = x->right;
}
z->parent = y;
if (y == Nil)
T = z;
else if (z->data.key < y->data.key)
y->left = z;
else y->right = z;
z->left = Nil; //指向哨兵
z->right = Nil;
z->data.Color = RED; //把插入结点置为红色
RBInsertFixUp(T, z); //维护红黑树性质
}
//插入数据后维护工作
void RBInsertFixUp(RBTree &T, RBTree z){
RBTree y = new RBTNode;
while (z->parent->data.Color == RED){
if (z->parent == z->parent->parent->left){
y = z->parent->parent->right; //y为z的叔结点
if (y->data.Color == RED){
z->parent->data.Color = BLACK; //情况一 z的叔结点y为红色
y->data.Color = BLACK;
z->parent->parent->data.Color = RED;
z = z->parent->parent;
if (z->parent == Nil){
break;
}
}
else if (z == z->parent->right){ //情况二 z的叔结点y为黑色且z为一个右孩
z = z->parent;
LeftRotate(T, z);
}
z->parent->data.Color = BLACK; //情况三 z的叔结点y为黑色且z为一个左孩
z->parent->parent->data.Color = RED;
if (z->parent->parent == Nil){
break;
}
RightRotate(T, z->parent->parent);
}
else if (z->parent == z->parent->parent->right){
y = z->parent->parent->left; //y为z的叔结点
if (y->data.Color == RED){
z->parent->data.Color = BLACK;
y->data.Color = BLACK;
z->parent->parent->data.Color = RED;
z = z->parent->parent;
if (z->parent == Nil){
break;
}
}
else if (z == z->parent->left){
z = z->parent;
RightRotate(T, z);
}
z->parent->data.Color = BLACK;
z->parent->parent->data.Color = RED;
if (z->parent->parent == Nil){
break;
}
LeftRotate(T, z->parent->parent);
}
}
T->data.Color = BLACK;
}
插入后如果父结点为黑色,则对红黑树性质没影响,如果该点为根结点,只要把该点置为黑色即可。
//情况一 z的叔结点y为红色,这时只要直接把叔结点和父结点均置为黑色,祖父结点置为红色,把z移到祖父结点,往上观察上方的情况即可。
//情况二 z的叔结点y为黑色且z为一个右孩,说明该树不能改变叔结点的颜色(否则会减少叔结点所在子树的黑色数),通过左旋变为情况三,利用情况三向右树送一个结点。
//情况三 z的叔结点y为黑色且z为一个左孩,直接右旋,把左树的一个结点送到该子树的根结点,根结点往右树移动。
--------------------------------------------------------------------------
//移动子树,把v移动到u处,u树将会分离出来
void Transplant(RBTree &T, RBTree u, RBTree v){
if (u->parent == Nil)
T = v;
else if (u == u->parent->left)
u->parent->left = v;
else u->parent->right = v;
v->parent = u->parent;
}
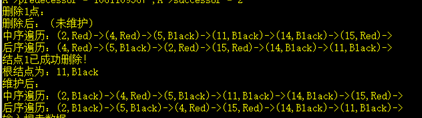
//删除数据结点
int Delete(RBTree &T, int e){
RBTree z = new RBTNode;
z = Search(T, e); //先收索该关键字是否存在
if (z == Nil){
return 0;
}
RBTree y = z, x;
TreeData q;
q.Color = y->data.Color; //记录y的原色(这里其实记录的是z的颜色)
if (z->left == Nil){ //左空,右树接上
x = z->right;
Transplant(T, z, z->right);
}
else if (z->right == Nil){ //右空,左树接上
x = z->left;
Transplant(T, z, z->left);
}
else{
y = Minimum(z->right); //z的后继
q.Color = y->data.Color; //记录y的原色
x = y->right;
if (y->parent == z)
x->parent = y; //防止移植后x的父结点指向z
else{
Transplant(T, y, y->right);
y->right = z->right;
y->right->parent = y;
}
Transplant(T, z, y);
y->left = z->left;
y->left->parent = y;
y->data.Color = z->data.Color; //用y代替z的位置后把y置为z的颜色(z为红,则y被置为红)
}
delete z;
if (q.Color == BLACK) //被删的z/y为黑色才要维护
RBDeleteFixUp(T, x); //x为指向y的原位置并更新删除后的位置
return 1;
}
//删除数据后维护工作
void RBDeleteFixUp(RBTree &T, RBTree x){
RBTree w = new RBTNode;
while (x != T&&x->data.Color == BLACK){ //顶替结点x不为根结点,且x(y)为黑色时才要调整位置
if (x == x->parent->left){
w = x->parent->right;
//case 1 兄弟结点为红色,把兄弟结点变为黑色,使x处补充一个黑色
if (w->data.Color == RED){
w->data.Color = BLACK; x->parent->data.Color = RED;
LeftRotate(T, x->parent);
w = x->parent->right;
}
//case 2 兄弟黑色,其孩子也是黑色,把兄弟变红色(减少旁边一个黑色结点数)
if (w->left->data.Color == BLACK&&w->right->data.Color == BLACK){
w->data.Color = RED;
x = x->parent;
if (x == T){
break;
}
}
//case 3 兄弟左孩为红,先调整为情况四,再补充结点
else if (w->right->data.Color == BLACK){
w->left->data.Color = BLACK;
w->data.Color = RED;
RightRotate(T, w);
w = x->parent->right;
}
//case 4 ,兄弟为黑,且右孩子为红,利用右树为左树补充一个黑结点
w->data.Color = x->parent->data.Color;
x->parent->data.Color = BLACK;
w->right->data.Color = BLACK;
LeftRotate(T, x->parent);
x = T;
}
else{ //对称操作
w = x->parent->left;
if (w->data.Color == RED){
w->data.Color = BLACK;
x->parent->data.Color = RED;
RightRotate(T, x->parent);
w = x->parent->left;
}
if (w->right->data.Color == BLACK&&w->right->data.Color == BLACK){
w->data.Color = RED;
x = x->parent;
if (x == T){
break;
}
}
else if (w->left->data.Color == BLACK){
w->right->data.Color = BLACK;
w->data.Color = RED;
LeftRotate(T, w);
w = x->parent->left;
}
w->data.Color = x->parent->data.Color;
x->parent->data.Color = BLACK;
w->right->data.Color = BLACK;
RightRotate(T, x->parent);
x = T;
}
}
x->data.Color = BLACK;
}
思考,这里的x,y,z是什么结点?
要注意,删除的为z结点,y为其对应的后继(y必定是一个没有左孩的结点),x为y的右孩。只有被删结点z为黑色才进入维护删除后,y顶替z的位置,x顶替y的位置,即在进行移植操作时,y和x的位置都会改为一个子树的根结点,使该子树可能少了一个黑色结点,违反性质5. 对每个结点,从该结点到其所有后代的叶结点的简单路径均包含相同数目的黑色结点。由于x的属性最终直接改为黑色,故x为双重颜色属性(红黑或黑黑)额外的颜色是针对结点,而非color属性本身。对于四种情况:
//case 1 兄弟结点为红色,把兄弟结点变为黑色,使x处补充一个黑色。
先因为w必须有黑色子结点,故可以改变w和x的父结点的颜色,对x的父结点进行一次左旋,而不违反红黑树的性质,通过这些操作使得情况1转换成情况2、3或者4处理。
//case 2 兄弟黑色,其孩子也是黑色,把兄弟变红色(减少旁边一个黑色结点数)。x和w的去掉一重黑色,那么x只有一重黑色,而w变为红色(即减少了旁边一个黑色结点数)。然后为了补偿从x和w中去掉的一重黑色,在原本为红色或黑色的x->parent重新添加一重黑色,并把x->parent作为新的x结点来重复while循环。
//case 3 兄弟左孩为红,先调整为情况四,再补充结点。首先交换w和其左孩子的颜色,然后对w进行右旋,这样就从情况3转换为情况4。
//case 4 ,x的兄弟为黑,且右孩子为红,利用右树为左树补充一个黑结点。修改一些颜色并对x->parent左旋,去掉x的额外黑色,使之变为黑色,且不破坏任何红黑树性质。把x设为根结点后,循环结束。
------------------------------------------------------------------------
//测试功能
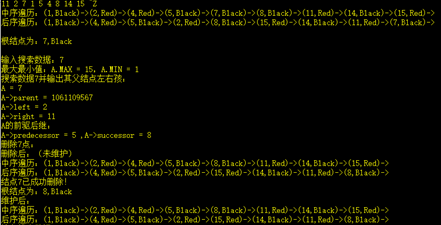
void test(RBTree T){
RBTree A = new RBTNode;
RBTree B = new RBTNode;
int n;
cout << "中序遍历:";
InOrderTraverse(T);
cout << endl;
cout << "后序遍历:";
PostOrderTraverse(T);
cout << endl << endl;
cout << "根结点为:" << T->data.key << "," << T->data.Color << endl;
for (;;){
cout << "输入搜索数据:";
cin >> n;
if (cin.fail()){
cin.clear();
cin.sync();
break;
}
A = Maximum(T);
cout << "最大最小值:" << "A.MAX = " << A->data.key;
A = Minimum(T);
cout << ",A.MIN = " << A->data.key << endl;
cout << "输入搜索数据:";
cin >> n;
cout << "搜索数据" << n << "并输出其父结点左右孩:" << endl;
A = Search(T, n);
cout << "A = " << A->data.key << endl;
cout << "A->parent = ";
if (A->parent)
cout << A->parent->data.key << endl;
else
cout << "ERROR!,NULL";
cout << "A->left = ";
if (A->left)
cout << A->left->data.key << endl;
else
cout << "ERROR!,NULL" << endl;
cout << "A->right = ";
if (A->right)
cout << A->right->data.key << endl;
else
cout << "ERROR!,NULL" << endl;
cout << "A的前驱后继:" << endl;
B = Predecessor(A);
if (B)
cout << "A->predecessor = " << B->data.key;
else
cout << "ERROR!,NULL" << endl;
B = Successor(A);
if (B)
cout << " ,A->successor = " << B->data.key << endl;
else
cout << "ERROR!,NULL" << endl;
}
}
//11 2 7 1 5 4 8 14 15
最后附上源代码:https://github.com/LRC-cheng/Algorithms_Practise.git