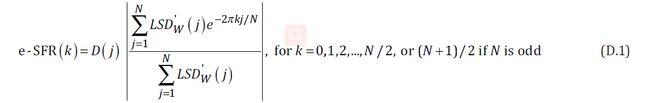SFR算法详解（二）——斜棱法

免责声明：仅供研究讨论，未经确认，相关内容严禁商用，若有错误，欢迎指正。

一、基于初版修正后产生的斜棱法(e-SFR)

(1) 选取斜棱所在的ROI区域进行初步分析。

在ISO12233中，这里对选取的ROI提出了几点要求，在经过逆OECF调整以后，选取的图像区域需要满足以下两点：

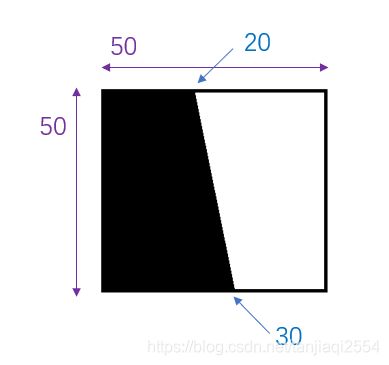
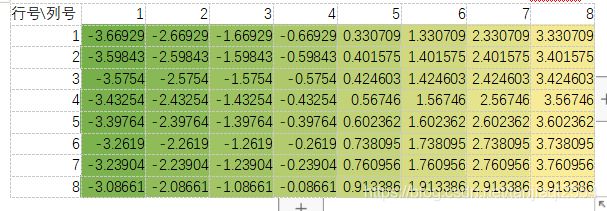
①选取的区域在后续计算中，顶部和底部区域的斜边分界点距离左右边沿不得少于2个像素，即不能太靠边，如下图我们选取的图像长宽为50*50，其顶部斜边分界距离左右边沿分别为20和30，底部分界距离左右边沿分别为30和20，均符合大于2的标准。

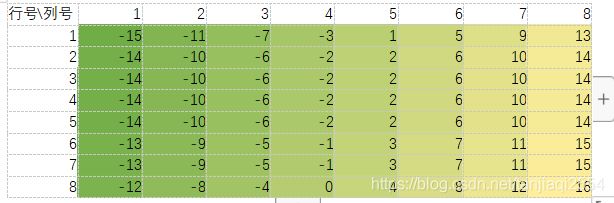
②我们选取的测试区域其边沿亮度调制比Modulation不得低于20%，什么意思呢，如下表：

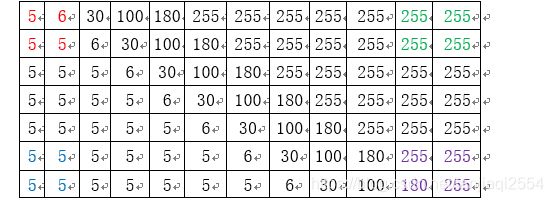
根据Mitre SFR 1.4开源代码示例中使用的做法，我们按2*2区域进行计算，有：

Avg_左上亮度均值 =  (5+6+5+5)/4.0 = 5.25

Avg_右上亮度均值 =  (255+255+255+255)/4.0 = 255.0

Avg_左下亮度均值 =  (5+5+5+5)/4.0 = 5.0

Avg_右下亮度均值 =  (255+255+180+255)/4.0 = 236.25

Modulation_顶部差异调制比 = (Avg_右上亮度均值- Avg_左上亮度均值)/( Avg_左上亮度均值+ Avg_右上亮度均值) = (255.0-5.25)/ (255.0+5.25)=95.97% >20%

Modulation_底部差异调制比 = (Avg_右下亮度均值- Avg_左下亮度均值)/( Avg_左下亮度均值+ Avg_右下亮度均值) = (236.25-5.0)/ (236.25+5.0)=95.85% >20%

由于以上列举的例子是一个垂直斜棱，因此我们只需考虑顶部和底部调制比即可，从上面的计算，我们得出，该区域符合相关标准。

(2) 通过逆光电转换函数(OECF)/逆Gamma校正对非线性的图像编码值(若为8位图像，即灰度值0-255)进行逆向线性化处理，将其还原为一个类CCD原始光电采样信号的序列。OECF可按ISO 14524规定的标准进行测量。

为了迎合OECF计算，新版SFR分辨率测试Chart特意在中间区域引入了16个灰阶测试块【ISO14524中使用的是20个】，以便于OECF计算。此外，各视场依次分布有斜方块，以便SFR进行后续计算。

这里提一下OECF/Gamma校正，读者也可参阅我的资源链中分享的一篇网上下载的文章https://download.csdn.net/download/tanjiaqi2554/10049457

这里我将图像模型抽象简化为以下几个角度进行说明：

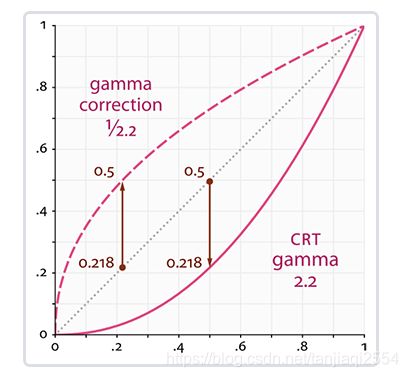
①人眼模型：相当于下图中的1/2.2 Gamma校正模型，人眼对暗处敏感，对亮处不敏感，即光信号经过人眼和大脑处理，暗处相对变亮，亮处相对变暗。

②摄像头光电传感器Sensor模型【未经后续Gamma校正ISP电路处理前】：即相当于下图中的黑色虚线部分，与光信号强度【光子数量】正相关，也就是说，亮即是亮，暗即是暗。

③摄像头ISP处理部分的Gamma校正模型：类似于人眼模型，将线性的光电信号，通过1/2.2Gamma校正为与人眼感知类似的灰度值输出。

④显示器模型：相当于下图中的2.2 Gamma校正模型，显示器为了迎合人眼特征，会让屏幕暗的时候，增长趋缓，亮的时候，增长趋陡，即让人眼反应屏幕亮暗变化时，不会觉得屏幕暗时，一下子被调亮了很多，又或者屏幕亮时，调了半天还感觉没反应。

下图引自博文https://learnopengl-cn.github.io/05%20Advanced%20Lighting/02%20Gamma%20Correction/

也许，上面我一下提供了太多的模型，不够直观，下面我又将各模型之间的相互嵌套关系绘制了一张总图，以便理解：

如上图，首先摄像头的Sensor接收到了光电信号，通过ISP做1/2.2 Gamma校正处理，转换为灰度值图像，此时该图像可存储在电脑中，当我们需要显示图像时，显示器（老式CRT一般是2.5，新的LCD一般2.2）通过2.2 Gamma的校正将灰度图重新转换回光信号。而我们的眼睛对光信号再进行了一遍1/2.2Gamma的处理，最后反应到大脑中。因此，整个光信号通过摄像头拍摄最终反映到我们大脑将经过如下过程：

人脑接收的信号 = ((光信号^(1/2.2))^2.2)^(1/2.2) = 光信号^(1/2.2)

而在ISO12233中规定，我们要用原始的Sensor光电信号【基于线性系统】，来参与计算SFR，因此，我们需要对ISP给我们的灰度图像，做如下的逆Gamma转换。基于ISP处理过程类似人眼，是将暗处相对调亮，亮处相对调暗，因此，逆回去应该是将暗处相对调暗，亮处相对调亮，但是这部分在Mitre SFR 1.4提供的代码中，跟我所述刚好是反的，关于这块个人觉得可能写错了吧。毕竟在计算斜边平移量S（r）时，ISO12233-2014中给出的公式S(r) = Cavg*(R/2-r)/m就是个错的，而在ISO12233-1999中的S(r) = Cavg+(R/2-r)/m则是对的，可见连ISO如今也并非那么严谨。

这里由于一般不会提供0-255级灰度值对应的每个光电信号值【实测灰阶值不是整数，也不够255个】，因此，我们一般要对测出的OECF数据，在0-255级整数灰度范围上进行线性补偿插值。

此外，对于一般手机模组厂来说，由于当前ISP是集成在手机主控ic上的，摄像模组直出的是Sensor原始Raw数据，因此，他们通常跳过该步骤，而是使用Raw插值出未经Gamma处理的灰度图像。如果您对以上过程仍存疑问，笔者再推荐几篇文章，它详细阐述了为什么显示器要采用非线性gamma校正后的输出，其中，作者给出的观点是它能保证我们在存储灰度图像时，通过延展暗部灰度，更多的保存暗部的细节，而又不用提高图像位深，增加存储空间消耗。

http://www.360doc.com/content/16/1020/14/496343_599870460.shtml

https://www.cambridgeincolour.com/tutorials/gamma-correction.htm

(3) 计算纵向斜棱质心，我们先逐行计算水平方向一阶微分，【左右相邻像素亮度差，即为水平方向一阶微分【梯度】，这部分在ISO文件中，采用的是卷积一个[-1/2,+1/2]的有限差分滤波器的方法，其实与邻差方法基本一致，只是相差一个两倍关系，以下是我参照开源代码Mitre SFR 1.4列举的案例】，举例如下：

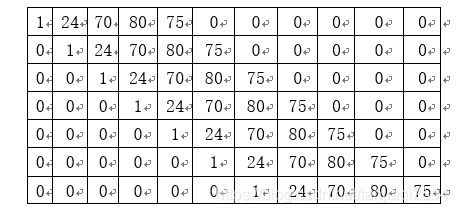
设原始经过逆OECF处理后的某ROI数据二维分布如下图，其亮度数据假设如下表所示【这里应当是逆OECF后的光电信号值，为方便，我以灰度为例，实际引入计算时的不一定转换为灰度】：

此时，经过水平一阶微分后，可得出如下表数据：

 

接下来，通过逐行计算水平列序号与该处微分值的卷积和，再除以该行积分累积总和，算得质心即各行斜棱交界处所在水平位置。如上表中第一行即:

CentroID =∑(x*array[0][x]) / ∑array[0][x]= (0*1+1*24+2*70+3*80+4*75+5*0+6*0+7*0+8*0+9*0+10*0 ) /( 1+24+70+80+75) = 704/250 = 2.816

依此类推，我们可以得到每行的CentroID 为如下序列：

[2.816,3.816,4.816,5.816,6.816,7.816,8.816]

公式为：

这里笔者通过阅读源码并参考文章https://mp.weixin.qq.com/s?__biz=MzIwNjU5NjcyNg%3D%3D&idx=1&mid=2247483800&sn=6f85015dfea597ea5059e44012f28be0，总结得sfrmat,Mitre SFR 1.4和Quick MTF方案中使用的有限差分滤波方案均为[-1,1],但在如下sfrmat中，会首先以图像宽度为周期，半宽度为中心，对各行应用一次汉明窗，计算初步的质心及拟合边缘曲线，接着取图像宽度为周期，拟合边缘位置为中心，再次对各行应用汉明窗，计算实际质心及拟合曲线，而Mitre SFR 1.4则只是计算质心，没有应用汉明窗。显然，应用汉明窗的方案将使得边缘检测更加稳定。

关于汉明窗可参阅https://blog.csdn.net/qq_32763149/article/details/84789141 https://www.cnblogs.com/MCSFX/p/10388045.html

(4) 对CentroID 进行线性回归拟合，得出斜棱分界线处的拟合回归方程y=mx+b。[其中因变量y为CentroID 值，自变量x为行号]

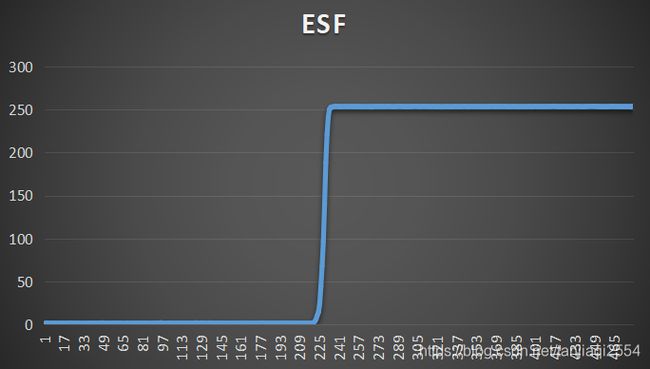
(5) 生成一个4倍超采样的边缘扩散函数序列：

这里我们有了斜棱方程，可以得出每一行上的斜棱位置，假设拟合曲线的斜棱质心如下所示，由于每一行上的像素与该行斜棱质心的水平距离并不都是整数，这给了我们实现亚像素采样的可能，不妨以0.25像素宽度为最小单位，对各行像素进行离散化归并。我们将水平距离属于同一档位的像素值进行累加平均，以得出该档位上的像素均值，如下所示：

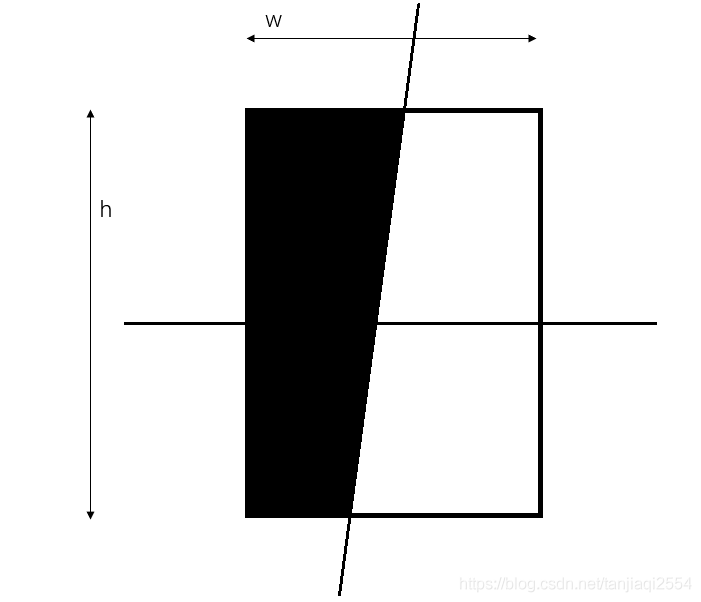
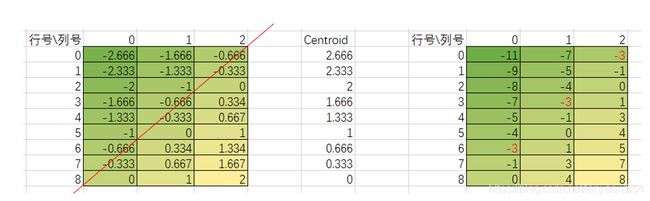
这里我以宽度8，高度8的一副图像来简化模型，根据各个像素位置到该行拟合Centroid的水平距离，我们可绘制如下表：

接着，我们以[-0.125,0.125]区间为0档位向正负方向延伸,其中[-0.375,-0.125]为-1档,[0.125,0.375]为+1档，依此类推，我们将上面各个位置的像素进行区间归档如下：

对归属于同一档的像素值进行累加平均有:【-15挡】=  0/1 = 0,【-14挡】=  (0+2+0+1)/4 = 0.75等等，依此类推。

最终我们将8行数据压缩归纳到了一行，得到一个基于距离的离散边缘扩散序列，我们的离散距离单位缩小为0.25个像素，当然你也可以乘以4倍，将单位归为1，但它代表的还是1/4个像素，而这也就是我们说的4倍超采样过程。

Ok，上述内容，你发现问题了，我们的各档位取样分配不均，并且你产生了疑问，会不会发生跳档现象，因此，ISO给我们附加了几条约束条件：

①边缘斜率不能高于1/4

②边缘斜率不能低于1/图像高度h

③计算数据高度应调整为(unsigned short)((long)(h*slope)*(1.0 / slope))整数。

Why?接下来我们逐一来分析：

先看第①条，我们不妨简化模型如下，令边缘斜率为1/3，发现遗失了档位【-10档】、【-6档】、【-2档】、【2档】、【6档】，可见，当斜边更接近于水平时，由于样本的周期为3【每次平移了1/3个像素，第四次平移将与第一次重叠】，小于4，实际上出现了周期性的重复，如【-3档】，因此我们将周期性的空缺一些档位。

同理，第②条中，由于我们每次平移将小于1/h个像素，实际上上下两行之间我们每次平移了1/slope个像素【这是在每个像素都是正方形模型的基础上】，因此，即使遍历整个h行，我们也不足以移动1个完整的像素，这势必也会导致周期的不完整，从而缺失一些档位，即导致平移的最大相位甚至不能达到采样周期【像素间隔】的1倍。

而对于第③条，我们应尽量保证遍历所有行时，数据总体移动的是完整的n个像素，即n倍于采样周期，若非如此，将导致在某些档位上代入多一个或几个周期计算均值，而另一些档位上则少一个或几个周期的信息，进而导致图像信息在空间上分配不均，同时导致各档位取样样本个数分配不均，这些势必也会影响我们最终的结果计算。

以上分析了这么多，简言之，该步操作就是通过以到斜边水平方向距离为基准，对多行数据进行分类归并，最终得到一行4倍于Sensor空间采样频率的序列，接下来，看一下ISO给出的公式，理解起来应该不难了：

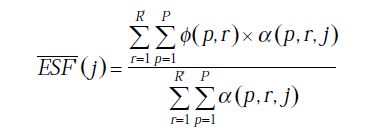
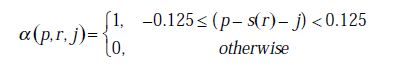
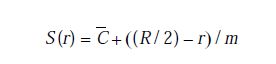，其中m为斜率slope,R为图像高度，φ(p,r)为p列r行的像素值，

S(r)为拟合边缘质心方程，j取{0,0.25,0.5,0.75,1...图像宽度w}，α(p,r,j)即是否纳入归档的因子，在区间范围内，值取1表示纳入该区间加权平均计算，值取0表示不纳入。

(6) 利用上述已得的4倍超采样的边缘扩散序列ESF，卷积一个有限差分滤波器[-1/2,0,1/2],得出线扩散序列LSF,这实际等同于对相邻2点ESF进行均值滤波后，再微分，即(a+b)/2-(b+c)/2=(a-c)/2。

 

(7) 这里需要再对LSF曲线应用一次汉明窗滤波，有两种方案，一种是sfrmat中使用的方法，即参照第(3)步所述方法，计算超采样ESF序列的CentroID【若对离散序列做了4倍放大，将步距由0.25放大到1，则取4倍图像宽度为周期】，以CentroID为中心，应用一次汉明窗。第二种方法是Mitre SFR 1.4/ISO中使用的方法，即遍历LSF曲线的极大值点，以该极大值点为分界，再在左右区域分别寻找各自的极大值点，然后取左右极值的几何中心【个人觉得不如就直接取极大值，多此一举的感觉，做法依然很粗糙】。

(8) 最后对滤波后的LSF曲线做DFT离散傅里叶变换，归一化，最终得到需要的eSFR曲线。关于傅里叶变换可参看视频https://www.bilibili.com/video/av51932171?t=628。

 

结语：本文主要参考ISO标准，主要对超采样做了一些说明，但尚有许多方面未进行深入探讨，例如以下：

1.为什么对ESF微分就得到了LSF，而对LSF进行傅里叶变换就能得到SFR曲线，ISO在制定标准时，为什么会选择这样的一条SFR曲线来作为衡量标准，理论依据是什么。

2.以上得到的SFR曲线与MTF曲线为什么存在联系，我们最后以怎样的方式来进行傅里叶变换，原因是什么。

关于以上内容的探讨，将不得不涉及MTF的定义，麦克劳林公式，正交函数系，傅里叶变换的推导，以及相关的傅里叶光学，欧拉公式，光学传递函数的定义等内容，对于以上SFR测试物理意义方面的探讨，或将在后续进行补充。