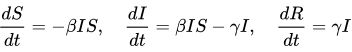【数学建模】Matlab实现SEIR模型
1974年Hoppensteadt首先在文[1]中建立和研究了具有年龄结构的传染病模型.至今,具有年龄结构的 传染病模型的研究已有许多成果(见[2]-[5]等),但这些模型大多不考虑染病年龄、潜伏期等对疾病传播 的影响.这就不能准确的描述某些具有较长潜伏期和病程的传染病(麻疹、肺结核等)的传播,因此建立 和研究具有生理年龄、潜伏期和染病年龄的传染病模型具有重要意义.目前,同时具有生理年龄、染病 年龄、潜伏期的传染病模型研究结果较少,只有一些特殊问题的结果,如文[6]-[7]研究了具有生理年龄和 染病年龄的传染病模型,文[8]-[9]建立和研究了同时具有潜伏期、染病年龄和生理年龄的无免疫型SEIS传 染病模型及其解的适定性.本文针对麻疹、肺结核等疾病,将人群分为S(易感类)、E(潜伏类)、I(染病 类)、R(治愈类)四类人群,利用K-M仓室模型原理(见文[10]),易建立同时具有生理年龄、染病年龄、潜 伏期的SEIR模型 。
这里总结了五个模型,分别是SI模型,SIS模型,SIR模型,SIRS模型,SEIR模型。
这几种模型的特点先介绍一下。
首先定义SEIR:
S为易感者 (Susceptible),指未得病者,但缺乏免疫能力,与感染者接触后容易受到感染;
E为暴露者 (Exposed),指接触过感染者,但暂无能力传染给其他人的人,对潜伏期长的传染病适用;
I为感病者 (Infective),指染上传染病的人,可以传播给 S 类成员,将其变为 E 类或 I 类成员;
R为康复者 (Recovered),指被隔离或因病愈而具有免疫力的人。如免疫期有限,R 类成员可以重新变为 S 类。
一、SI模型
该模型只考虑易感者和感病者,感病者不断去感染易感者。
随着时间推移,该模型感染者越来越多直到所有人都感染。
其微分方程为:
其中beta为感染率。
二、SIS模型
该模型依然只考虑易感者和感病者,感病者不断去感染易感者,这里感病者会得到治疗恢复成易感者,不过恢复后依然可能得病。
随着时间推移,该模型感染者和易感者会达到动态平衡。
其微分方程为:
其中beta为感染率,gamma为治愈率。
三、SIR模型
该模型考虑易感者、感病者与康复者,其中感病者不断感染易感者,而感病者又不断接受治疗成为康复者,康复者因为得到抗体不会再成为易感者。
随着时间推移,该模型康复者越来越多,最终所有人都成为康复者。
其微分方程为:
其中beta为感染率,gamma为治愈率。
四、SIRS模型
该模型考虑易感者、感病者与康复者,其中感病者不断感染易感者,而感病者不断接受治疗成为康复者,康复者获得抗体能够抵抗一段时间,不过最终还是会成为易感者。
该模型和SIS模型很像,区别就是康复者能够抵抗一段时间,也就是有一定的复感率,而SIS模型的复感率为1。
随着时间推移,该模型同样会达到一个动态平衡。
其微分方程为:
其中beta为感染率,gamma为治愈率,alpha为复感率。
五、SEIR模型
该模型四种参与者全部考虑,其中感病者不断感染易感者,易感者得到病毒会成为潜伏者,潜伏者依然能够使易感者感染,潜伏者有一定概率自己痊愈,感染者接受治疗也能够痊愈,痊愈后不再能够感染该病。
随着时间推移,该模型最终也是所有人都会成为康复者。
其微分方程为:
其中beta为感染率,gamma1为潜伏期康复率,gamma2为患者康复率,alpha为潜伏期转阳率。
function Message_Spread_Mode
tic
load 'Data\Link.txt'; %读入连接矩阵
% load '\Data\Point_X.txt'; %读入横坐标
% load '\Data\Point_Y.txt'; %读入纵坐标
%-------------------------------------------------------------------------%
%状态分布及状态转移概率SEIR
%0:易感状态S(Susceptible) P_0_1; (P_0_3:预免疫系数)
%1:潜伏状态E(Exposed) P_1_0;P_1_2;P_1_3
%2:染病状态I(Infected) P_2_0;P_2_3
%3:免疫状态R(Recovered) P_3_0
%-------------------------------------------------------------------------%
%计算各用户节点的度
De=sum(Link); %用户节点的度
%------------——————----参数设置与说明--------------------------------%
[M N]=size(Link); %连接矩阵的规模
I_E=0.6; %潜伏期E用户的传染强度
I_I=0.9; %发病期I用户的传染强度
lamda=sum(De)/M; %用户单位时间内平均发送信息的数量
%P_m1:用户预免疫系数
%State:用户所处状态State=zeros(1,M);0:表示易感状态(Susceptible)
%---------------------------------1---------------------------------------%
%先讨论用户预免疫系数P_m1对病毒传播的影响
TimeStep=50;%input('短信网络内病毒传播模拟时间:');
P_m1=[0.1,0.5,0.9]; %用户预免疫系数
% State=zeros(TimeStep,M); %用户的状态
G_t=5; %G_t:用户的免疫持续时间,反映了病毒的变异频率
F_t=5; %F_t:用户从发现病毒到杀毒并升级病毒库的时间
for i=1:length(P_m1)
TimeLong_F=zeros(1,M); %用户处于染病期的时间长短
TimeLong_E=zeros(1,M); %用户处于潜伏期的时间长短
Sta=zeros(1,M); %用户的状态
%进行预免疫设定
for j=1:M
if rand(1)<=P_m1(i)
Sta(j)=3; %进入免疫状态
TimeLong_E(j)=1; %出入潜伏期的时间为1
else
continue;
end
end
%状态转换
%初始随机选择一个节点为病源点(此时不能选处于免疫状态的点)
%问题:节点度大小存在差别,可能模拟出来的结果有出于
% 为避免这个问题,我们取度最大的节点为病源节点,如果已免疫,则选次大的,一次下去
[Number,Sta]=Select_Infected_Point(M,Sta,De);
%Number:病源节点
%State :确定病源节点以后的节点状态矩阵
State=zeros(TimeStep,M);
Number_State=zeros(4,TimeStep); %用户处于个状态的统计数量
for t=1:TimeStep
if t==1
State(t,:)=Sta;
else
%模拟每个用户节点的状态
for j=1:M
%判断用户节点处于什么状态,然后根据其状态确定其转变情况
if State(t-1,j)==0 %此时处于易感状态0,可能向潜伏期转移
Num=Select_Number_Near(j,Link); %找出节点j的邻居节点
P=zeros(1,length(Num)); %邻居节点感染该节点的概率
for k=1:length(Num)
if State(t-1,Num(k))==1 %节点处于潜伏期E(1)
P(k)=I_E/De(Num(k))*sum((lamda.^([1:De(Num(k))]).*exp(-lamda))./...
(factorial([1:De(Num(k))]-1)));
else
if State(t-1,Num(k))==2 %节点处于染病期I(2)
P(k)=I_I/De(Num(k))*sum((lamda.^([1:De(Num(k))]).*exp(-lamda))./(factorial([1:De(Num(k))]-1)));
else
continue;
end
end
end
P_0_1=max(P); %节点感染病毒的概率
if rand<=P_0_1 %此时节点进入潜伏期
State(t,j)=1;
else
State(t,j)=State(t-1,j);
end
else
if State(t-1,j)==1 %此时处于潜伏状态E,可能向易感S,染病I和免疫R转移
if rand<=1/(1+exp(-De(j))) %向染病状态I转移
State(t,j)=2;
TimeLong_F(j)=TimeLong_F(j)+1; %用户j处于染病状态的时间长短
else
if rand<=1/(1+exp(-De(j))) %向易感状态S转移
State(t,j)=0;
else
if rand<=1/(1+exp(-De(j))) %向免疫状态R转移
State(t,j)=3;
TimeLong_E(j)=TimeLong_E(j)+1; %免疫时间增加1
else
State(t,j)=State(t-1,j); %状态不变,依然为潜伏期E(1)
end
end
end
else
if State(t-1,j)==2 %此时处于欺染病状态I,可能向易感S,免疫R转移
if TimeLong_F(j)<=F_t %表示此时用户不对病毒进行任何处理
State(t,j)=State(t-1,j); %此时用户维持在原状态I
TimeLong_F(j)=TimeLong_F(j)+2;
else
%此时用户对进行杀毒并升级病毒库,进入免疫状态R
State(t,j)=3;
TimeLong_F(j)=0; %处于感染期(中毒状态)的时间长度
TimeLong_E(j)=1; %进入免疫期的时间长度
end
else
%此时用户处于免疫期
if TimeLong_E<=G_t %病毒此时并未突变,维持原状态R(免疫状态)
State(t,j)=State(t-1,j);
TimeLong_E(j)=TimeLong_E(j)+1; %处于免疫期的时间增加
else
if rand<=1/G_t %病毒突变,状态转移为易感状态S
State(t,j)=0;
TimeLong_E(j)=0;
else
%此时用户状态依然不变
State(t,j)=State(t-1,j);
TimeLong_E(j)=TimeLong_E(j)+1; %处于免疫期的时间增加
end
end
end
end
end
end
end
%统计各状态的节点数量
Number_State(1,t)=sum(State(t,:)==0);%处于易感状态S的总节点数量
Number_State(2,t)=sum(State(t,:)==1);%处于易感状态E的总节点数量
Number_State(3,t)=sum(State(t,:)==2);%处于易感状态I的总节点数量
Number_State(4,t)=sum(State(t,:)==3);%处于易感状态R的总节点数量
figure(i)
if rem(t,3)==0
plot([t-1 t],[Number_State(1,t-1) Number_State(1,t)],'md-'),hold on
plot([t-1 t],[Number_State(2,t-1) Number_State(2,t)],'gh:'),hold on
plot([t-1 t],[Number_State(3,t-1) Number_State(3,t)],'bs-.'),hold on
plot([t-1 t],[Number_State(4,t-1) Number_State(4,t)],'k.-'),hold on
else
continue;
end
legend('易感状态Susceptible','潜伏状态Exposed','染病状态Infected','免疫状态Recovered')
xlabel('模拟时间')
ylabel('各状态的用户数量')
end
end
P_m1=0.3; %用户预免疫系数
% State=zeros(TimeStep,M); %用户的状态
% G_t=5; %G_t:用户的免疫持续时间,反映了病毒的变异频率
G_t=[1,5,9];
F_t=5; %F_t:用户从发现病毒到杀毒并升级病毒库的时间
for i=1:length(G_t)
TimeLong_F=zeros(1,M); %用户处于染病期的时间长短
TimeLong_E=zeros(1,M); %用户处于潜伏期的时间长短
Sta=zeros(1,M); %用户的状态
%进行预免疫设定
for j=1:M
if rand(1)<=P_m1
Sta(j)=3; %进入免疫状态
TimeLong_E(j)=1; %出入潜伏期的时间为1
else
continue;
end
end
%状态转换
%初始随机选择一个节点为病源点(此时不能选处于免疫状态的点)
%问题:节点度大小存在差别,可能模拟出来的结果有出于
% 为避免这个问题,我们取度最大的节点为病源节点,如果已免疫,则选次大的,一次下去
[Number,Sta]=Select_Infected_Point(M,Sta,De);
%Number:病源节点
%State :确定病源节点以后的节点状态矩阵
State=zeros(TimeStep,M);
Number_State=zeros(4,TimeStep); %用户处于个状态的统计数量
for t=1:TimeStep
if t==1
State(t,:)=Sta;
else
%模拟每个用户节点的状态
for j=1:M
%判断用户节点处于什么状态,然后根据其状态确定其转变情况
if State(t-1,j)==0 %此时处于易感状态0,可能向潜伏期转移
Num=Select_Number_Near(j,Link); %找出节点j的邻居节点
P=zeros(1,length(Num)); %邻居节点感染该节点的概率
for k=1:length(Num)
if State(t-1,Num(k))==1 %节点处于潜伏期E(1)
P(k)=I_E/De(Num(k))*sum((lamda.^([1:De(Num(k))]).*exp(-lamda))./...
(factorial([1:De(Num(k))]-1)));
else
if State(t-1,Num(k))==2 %节点处于染病期I(2)
P(k)=I_I/De(Num(k))*sum((lamda.^([1:De(Num(k))]).*exp(-lamda))./...
(factorial([1:De(Num(k))]-1)));
else
continue;
end
end
end
P_0_1=max(P); %节点感染病毒的概率
if rand<=P_0_1 %此时节点进入潜伏期
State(t,j)=1;
else
State(t,j)=State(t-1,j);
end
else
if State(t-1,j)==1 %此时处于潜伏状态E,可能向易感S,染病I和免疫R转移
if rand<=1/(1+exp(-De(j))) %向染病状态I转移
State(t,j)=2;
TimeLong_F(j)=TimeLong_F(j)+1; %用户j处于染病状态的时间长短
else
if rand<=1/(1+exp(-De(j))) %向易感状态S转移
State(t,j)=0;
else
if rand<=1/(1+exp(-De(j))) %向免疫状态R转移
State(t,j)=3;
TimeLong_E(j)=TimeLong_E(j)+1; %免疫时间增加1
else
State(t,j)=State(t-1,j); %状态不变,依然为潜伏期E(1)
end
end
end
else
if State(t-1,j)==2 %此时处于欺染病状态I,可能向易感S,免疫R转移
if TimeLong_F(j)<=F_t %表示此时用户不对病毒进行任何处理
State(t,j)=State(t-1,j); %此时用户维持在原状态I
TimeLong_F(j)=TimeLong_F(j)+2;
else
%此时用户对进行杀毒并升级病毒库,进入免疫状态R
State(t,j)=3;
TimeLong_F(j)=0; %处于感染期(中毒状态)的时间长度
TimeLong_E(j)=1; %进入免疫期的时间长度
end
else
%此时用户处于免疫期
if TimeLong_E<=G_t(i) %病毒此时并未突变,维持原状态R(免疫状态)
State(t,j)=State(t-1,j);
TimeLong_E(j)=TimeLong_E(j)+1; %处于免疫期的时间增加
else
if rand<=1/G_t(i) %病毒突变,状态转移为易感状态S
State(t,j)=0;
TimeLong_E(j)=0;
else
%此时用户状态依然不变
State(t,j)=State(t-1,j);
TimeLong_E(j)=TimeLong_E(j)+1; %处于免疫期的时间增加
end
end
end
end
end
end
end
%统计各状态的节点数量
Number_State(1,t)=sum(State(t,:)==0);%处于易感状态S的总节点数量
Number_State(2,t)=sum(State(t,:)==1);%处于易感状态E的总节点数量
Number_State(3,t)=sum(State(t,:)==2);%处于易感状态I的总节点数量
Number_State(4,t)=sum(State(t,:)==3);%处于易感状态R的总节点数量
figure(i+5)
if rem(t,3)==0
plot([t-1 t],[Number_State(1,t-1) Number_State(1,t)],'md-'),hold on
plot([t-1 t],[Number_State(2,t-1) Number_State(2,t)],'gh:'),hold on
plot([t-1 t],[Number_State(3,t-1) Number_State(3,t)],'bs-.'),hold on
plot([t-1 t],[Number_State(4,t-1) Number_State(4,t)],'k.-'),hold on
else
continue;
end
legend('易感状态Susceptible','潜伏状态Exposed','染病状态Infected','免疫状态Recovered')
xlabel('模拟时间')
ylabel('各状态的用户数量')
end
end
P_m1=0.3; %用户预免疫系数
% State=zeros(TimeStep,M); %用户的状态
% G_t=5; %G_t:用户的免疫持续时间,反映了病毒的变异频率
G_t=5;
F_t=[1,5,9]; %F_t:用户从发现病毒到杀毒并升级病毒库的时间
for i=1:length(F_t)
TimeLong_F=zeros(1,M); %用户处于染病期的时间长短
TimeLong_E=zeros(1,M); %用户处于潜伏期的时间长短
Sta=zeros(1,M); %用户的状态
%进行预免疫设定
for j=1:M
if rand(1)<=P_m1
Sta(j)=3; %进入免疫状态
TimeLong_E(j)=1; %出入潜伏期的时间为1
else
continue;
end
end
%状态转换
%初始随机选择一个节点为病源点(此时不能选处于免疫状态的点)
%问题:节点度大小存在差别,可能模拟出来的结果有出于
% 为避免这个问题,我们取度最大的节点为病源节点,如果已免疫,则选次大的,一次下去
[Number,Sta]=Select_Infected_Point(M,Sta,De);
%Number:病源节点
%State :确定病源节点以后的节点状态矩阵
State=zeros(TimeStep,M);
Number_State=zeros(4,TimeStep); %用户处于个状态的统计数量
for t=1:TimeStep
if t==1
State(t,:)=Sta;
else
%模拟每个用户节点的状态
for j=1:M
%判断用户节点处于什么状态,然后根据其状态确定其转变情况
if State(t-1,j)==0 %此时处于易感状态0,可能向潜伏期转移
Num=Select_Number_Near(j,Link); %找出节点j的邻居节点
P=zeros(1,length(Num)); %邻居节点感染该节点的概率
for k=1:length(Num)
if State(t-1,Num(k))==1 %节点处于潜伏期E(1)
P(k)=I_E/De(Num(k))*sum((lamda.^([1:De(Num(k))]).*exp(-lamda))./...
(factorial([1:De(Num(k))]-1)));
else
if State(t-1,Num(k))==2 %节点处于染病期I(2)
P(k)=I_I/De(Num(k))*sum((lamda.^([1:De(Num(k))]).*exp(-lamda))./...
(factorial([1:De(Num(k))]-1)));
else
continue;
end
end
end
P_0_1=max(P); %节点感染病毒的概率
if rand<=P_0_1 %此时节点进入潜伏期
State(t,j)=1;
else
State(t,j)=State(t-1,j);
end
else
if State(t-1,j)==1 %此时处于潜伏状态E,可能向易感S,染病I和免疫R转移
if rand<=1/(1+exp(-De(j))) %向染病状态I转移
State(t,j)=2;
TimeLong_F(j)=TimeLong_F(j)+1; %用户j处于染病状态的时间长短
else
if rand<=1/(1+exp(-De(j))) %向易感状态S转移
State(t,j)=0;
else
if rand<=1/(1+exp(-De(j))) %向免疫状态R转移
State(t,j)=3;
TimeLong_E(j)=TimeLong_E(j)+1; %免疫时间增加1
else
State(t,j)=State(t-1,j); %状态不变,依然为潜伏期E(1)
end
end
end
else
if State(t-1,j)==2 %此时处于欺染病状态I,可能向易感S,免疫R转移
if TimeLong_F(j)<=F_t(i) %表示此时用户不对病毒进行任何处理
State(t,j)=State(t-1,j); %此时用户维持在原状态I
TimeLong_F(j)=TimeLong_F(j)+2;
else
%此时用户对进行杀毒并升级病毒库,进入免疫状态R
State(t,j)=3;
TimeLong_F(j)=0; %处于感染期(中毒状态)的时间长度
TimeLong_E(j)=1; %进入免疫期的时间长度
end
else
%此时用户处于免疫期
if TimeLong_E<=G_t %病毒此时并未突变,维持原状态R(免疫状态)
State(t,j)=State(t-1,j);
TimeLong_E(j)=TimeLong_E(j)+1; %处于免疫期的时间增加
else
if rand<=1/G_t %病毒突变,状态转移为易感状态S
State(t,j)=0;
TimeLong_E(j)=0;
else
%此时用户状态依然不变
State(t,j)=State(t-1,j);
TimeLong_E(j)=TimeLong_E(j)+1; %处于免疫期的时间增加
end
end
end
end
end
end
end
%统计各状态的节点数量
Number_State(1,t)=sum(State(t,:)==0);%处于易感状态S的总节点数量
Number_State(2,t)=sum(State(t,:)==1);%处于易感状态E的总节点数量
Number_State(3,t)=sum(State(t,:)==2);%处于易感状态I的总节点数量
Number_State(4,t)=sum(State(t,:)==3);%处于易感状态R的总节点数量
figure(i+10)
if rem(t,3)==0
plot([t-1 t],[Number_State(1,t-1) Number_State(1,t)],'md-'),hold on
plot([t-1 t],[Number_State(2,t-1) Number_State(2,t)],'gh:'),hold on
plot([t-1 t],[Number_State(3,t-1) Number_State(3,t)],'bs-.'),hold on
plot([t-1 t],[Number_State(4,t-1) Number_State(4,t)],'k.-'),hold on
else
continue;
end
legend('易感状态Susceptible','潜伏状态Exposed','染病状态Infected','免疫状态Recovered')
xlabel('模拟时间')
ylabel('各状态的人口数量')
end
end
toc
![]()
具体代码如下:
qq 1575304183