OLS回归分析原理实战及结果解析-python3

OLS 回归

变量之间存在着相关关系，比如，人的身高和体重之间存在着关系，一般来说，人高一些，体重要重一些，身高和体重之间存在的是不确定性的相关关系。回归分析是研究相关关系的一种数学工具，它能帮助我们从一个变量的取值区估计另一个变量的取值。

OLS(最小二乘法)主要用于线性回归的参数估计，它的思路很简单，就是求一些使得实际值和模型估值之差的平方和达到最小的值，将其作为参数估计值。就是说，通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法可用于曲线拟合，其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

假设我们有回归模型
Y=β0+β1X1+⋯+βnXn+ε,
并且有 k 组数据 (y(t),x_{1}(t) ,…,x_{n}(t) )_{t=1}^{k}。OLS 回归用于计算回归系数 βi 的估值 b0,b1,…,bn，使误差平方

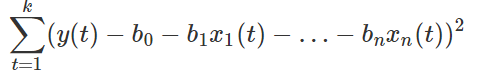
最小化。
statsmodels.OLS 的输入有 (endog, exog, missing, hasconst) 四个，我们现在只考虑前两个。第一个输入 endog 是回归中的反应变量（也称因变量），是上面模型中的 y(t), 输入是一个长度为 k 的 array。第二个输入 exog 则是回归变量（也称自变量）的值，即模型中的x1(t),…,xn(t)。但是要注意，statsmodels.OLS 不会假设回归模型有常数项，所以我们应该假设模型是

并且在数据中，对于所有 t=1,…,k，设置 x0(t)=1。因此，exog的输入是一个 k×(n+1) 的 array，其中最左一列的数值全为 1。往往输入的数据中，没有专门的数值全为1的一列，Statmodels 有直接解决这个问题的函数：sm.add_constant()。它会在一个 array 左侧加上一列 1。（本文中所有输入 array 的情况也可以使用同等的 list、pd.Series 或 pd.DataFrame。）
确切地说，statsmodels.OLS 是 statsmodels.regression.linear_model 里的一个函数（从这个命名也能看出，statsmodel 有很多很多功能，其中的一项叫回归）。它的输出结果是一个 statsmodels.regression.linear_model.OLS，只是一个类，并没有进行任何运算。在 OLS 的模型之上调用拟合函数 fit()，才进行回归运算，并且得到 statsmodels.regression.linear_model.RegressionResultsWrapper，它包含了这组数据进行回归拟合的结果摘要。调用 params 可以查看计算出的回归系数 b0,b1,…,bn。

简单的线性回归

上面的介绍绕了一个大圈圈，现在我们来看一个例子，假设回归公式是:

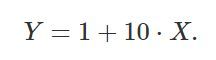
我们从最简单的一元模型开始，虚构一组数据。首先设定数据量，也就是上面的 k 值。

nsample = 100

然后创建一个 array，是上面的 x1 的数据。这里，我们想要 x1 的值从 0 到 10 等差排列。

x = np.linspace(0, 10, nsample)

使用 sm.add_constant() 在 array 上加入一列常项1。

X = sm.add_constant(x)

然后设置模型里的 β0,β1，这里要设置成 1,10。

beta = np.array([1, 10])

然后还要在数据中加上误差项，所以生成一个长度为k的正态分布样本。

e = np.random.normal(size=nsample)

由此，我们生成反应项 y(t)。

y = np.dot(X, beta) + e

好嘞，在反应变量和回归变量上使用 OLS() 函数。

model = sm.OLS(y,X)

然后获取拟合结果。

results = model.fit()

再调取计算出的回归系数。

print(results.params)

得到

[ 1.04510666, 9.97239799]

和实际的回归系数非常接近。

当然，也可以将回归拟合的摘要全部打印出来。

print(results.summary())

结果解释在本章最后
中间偏下的 coef 列就是计算出的回归系数。

我们还可以将拟合结果画出来。先调用拟合结果的 fittedvalues 得到拟合的 y 值。

y_fitted = results.fittedvalues

然后使用 matplotlib.pyploft 画图。首先设定图轴，图片大小为 8×6。

fig, ax = plt.subplots(figsize=(8,6))

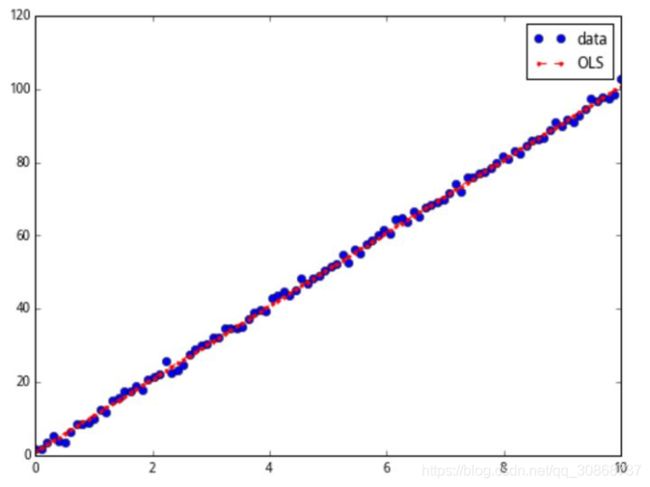
画出原数据，图像为圆点，默认颜色为蓝。

ax.plot(x, y, 'o', label='data')

画出拟合数据，图像为红色带点间断线。

ax.plot(x, y_fitted, 'r--.',label='OLS')

放置注解。

ax.legend(loc='best')

得到

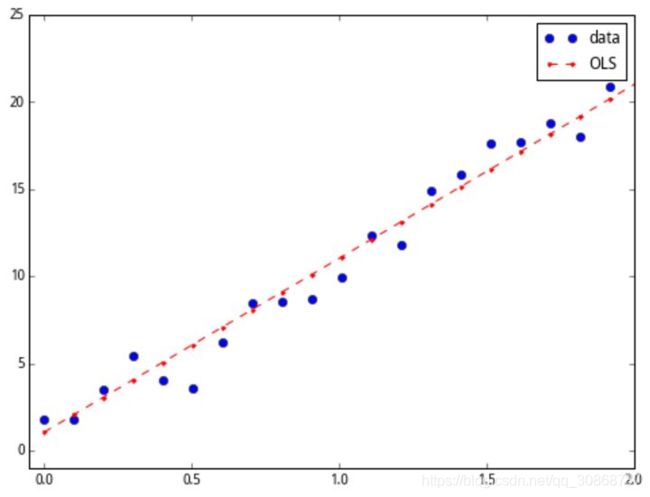
在大图中看不清细节，我们在 0 到 2 的区间放大一下，可以见数据和拟合的关系。

加入改变坐标轴区间的指令

ax.axis((-0.05, 2, -1, 25))
plt.show()

高次模型的回归

假设反应变量 Y 和回归变量 X 的关系是高次的多项式，即

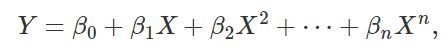
我们依然可以使用 OLS 进行线性回归。但前提条件是，我们必须知道 X 在这个关系中的所有次方数；比如，如果这个公式里有一个 x^{2}.5项，但我们对此并不知道，那么用线性回归的方法就不能得到准确的拟合。

虽然 X 和 Y 的关系不是线性的，但是 Y 和 X,X^{2} ,…X^{n} 的关系是高元线性的。也就是说，只要我们把高次项当做其他的自变量，即设 X_{1} =X,X_{2} =X^{2} ,…,X^{n}。那么，对于线性公式

可以进行常规的 OLS 回归，估测出每一个回归系数 βi。可以理解为把一元非线性的问题映射到高元，从而变成一个线性关系。
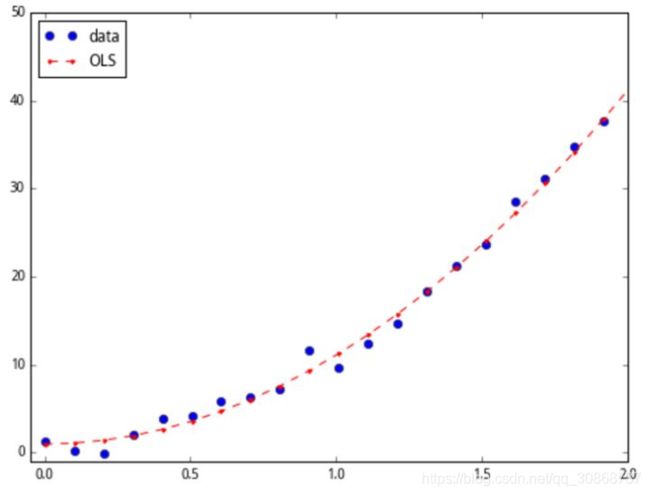
下面以

为例做一次演示。
首先设定数据量，也就是上面的 k 值。

nsample = 100

然后创建一个 array，是上面的 x1 的数据。这里，我们想要 x1 的值从 0 到 10 等差排列。

x = np.linspace(0, 10, nsample)

再创建一个 k×2 的 array，两列分别为 x1 和 x2。我们需要 x2 为 x1 的平方。

X = np.column_stack((x, x**2))

使用 sm.add_constant() 在 array 上加入一列常项 1。

X = sm.add_constant(X)

然后设置模型里的 β0,β1,β2，我们想设置成 1,0.1,10。

beta = np.array([1, 0.1, 10])

然后还要在数据中加上误差项，所以生成一个长度为k的正态分布样本。

e = np.random.normal(size=nsample)

由此，我们生成反应项 y(t)，它与 x1(t) 是二次多项式关系。

y = np.dot(X, beta) + e

在反应变量和回归变量上使用 OLS() 函数。

model = sm.OLS(y,X)

然后获取拟合结果。

results = model.fit()

再调取计算出的回归系数。

print(results.params)

得到

[ 0.95119465, 0.10235581, 9.9998477]

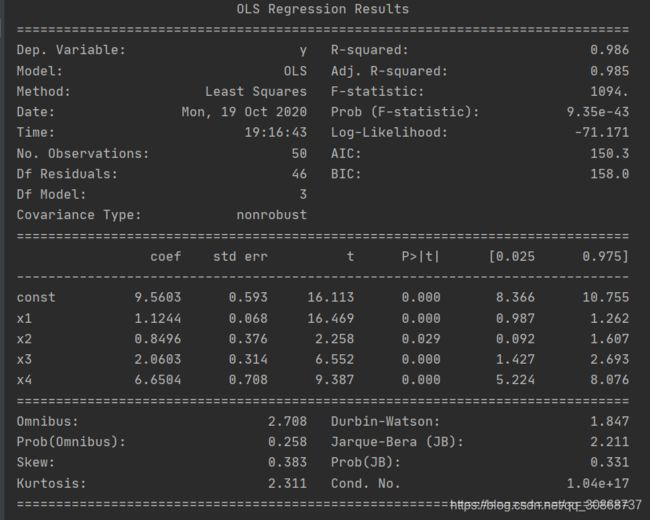
获取全部摘要

print(results.summary())

得到

拟合结果图如下

在横轴的 [0,2] 区间放大，可以看到

哑变量

一般而言，有连续取值的变量叫做连续变量，它们的取值可以是任何的实数，或者是某一区间里的任何实数，比如股价、时间、身高。但有些性质不是连续的，只有有限个取值的可能性，一般是用于分辨类别，比如性别、婚姻情况、股票所属行业，表达这些变量叫做分类变量。在回归分析中，我们需要将分类变量转化为哑变量(dummy variable)。

如果我们想表达一个有 d 种取值的分类变量，那么它所对应的哑变量的取值是一个 d 元组（可以看成一个长度为 d 的向量），其中有一个元素为 1，其他都是 0。元素呈现出 1 的位置就是变量所取的类别。比如说，某个分类变量的取值是 {a,b,c,d}，那么类别 a 对应的哑变量是(1,0,0,0)，b 对应 (0,1,0,0)，c 对应 (0,0,1,0)，d 对应 (0,0,0,1)。这么做的用处是，假如 a、b、c、d 四种情况分别对应四个系数 β0,β1,β2,β3，设 (x0,x1,x2,x3) 是一个取值所对应的哑变量，那么

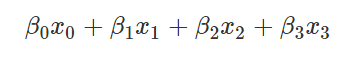
可以直接得出相应的系数。可以理解为，分类变量的取值本身只是分类，无法构成任何线性关系，但是若映射到高元的 0,1 点上，便可以用线性关系表达，从而进行回归。

Statsmodels 里有一个函数 categorical() 可以直接把类别 {0,1,…,d-1} 转换成所对应的元组。确切地说，sm.categorical() 的输入有 (data, col, dictnames, drop) 四个。其中，data 是一个 k×1 或 k×2 的 array，其中记录每一个样本的分类变量取值。drop 是一个 Bool值，意义为是否在输出中丢掉样本变量的值。中间两个输入可以不用在意。这个函数的输出是一个k×d 的 array（如果 drop=False，则是k×(d+1)），其中每一行是所对应的样本的哑变量；这里 d 是 data 中分类变量的类别总数。

我们来举一个例子。这里假设一个反应变量 Y 对应连续自变量 X 和一个分类变量 Z。常项系数为 10，XX 的系数为 1；Z 有 {a,b,c}三个种类，其中 a 类有系数 1，b 类有系数 3，c 类有系数 8。也就是说，将 Z 转换为哑变量 (Z1,Z2,Z3)，其中 Zi 取值于 0,1，有线性公式

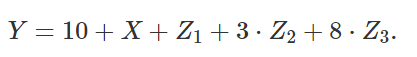
可以用常规的方法进行 OLS 回归。
我们按照这个关系生成一组数据来做一次演示。先定义样本数量为 50。

nsample = 50

设定分类变量的 array。前 20 个样本分类为 a。

groups = np.zeros(nsample, int)

之后的 20 个样本分类为 b。

groups[20:40] = 1

最后 10 个是 c 类。

groups[40:] = 2

转变成哑变量。

dummy = sm.categorical(groups, drop=True)

创建一组连续变量，是 50 个从 0 到 20 递增的值。

x = np.linspace(0, 20, nsample)

将连续变量和哑变量的 array 合并，并加上一列常项。

X = np.column_stack((x, dummy))
X = sm.add_constant(X)

定义回归系数。我们想设定常项系数为 10，唯一的连续变量的系数为 1，并且分类变量的三种分类 a、b、c 的系数分别为 1,3,8。

beta = [10, 1, 1, 3, 8]

再生成一个正态分布的噪音样本。

e = np.random.normal(size=nsample)

最后，生成反映变量。

y = np.dot(X, beta) + e

得到了虚构数据后，放入 OLS 模型并进行拟合运算。

result = sm.OLS(y,X).fit()
print(result.summary())

得到

再画图出来

fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, y, 'o', label="data")
ax.plot(x, result.fittedvalues, 'r--.', label="OLS")
ax.legend(loc='best')
plt.show()

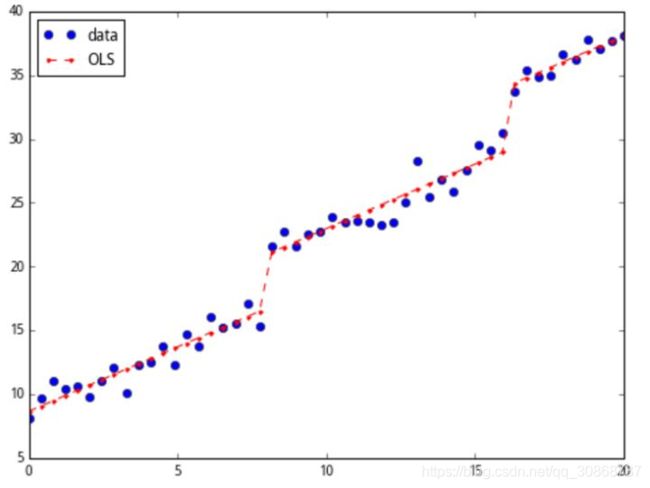
这里要指出，哑变量是和其他自变量并行的影响因素，也就是说，哑变量和原先的 x 同时影响了回归的结果。初学者往往会误解这一点，认为哑变量是一个选择变量：也就是说，上图中给出的回归结果，是在只做了一次回归的情况下完成的，而不是分成３段进行３次回归。哑变量的取值藏在其他的三个维度中。可以理解成：上图其实是将高元的回归结果映射到平面上之后得到的图。

简单应用

我们来做一个非常简单的实际应用。设 x 为上证指数的日收益率，y 为深证成指的日收益率。通过对股票市场的认知，我们认为 x 和 y 有很强的线性关系。因此可以假设模型

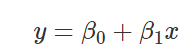
并使用 Statsmodels 包进行 OLS 回归分析。
我们取上证指数和深证成指一年中的收盘价。

data = get_price(['000001.XSHG', '399001.XSHE'], start_date='2015-01-01', end_date='2016-01-01', frequency='daily', fields=['close'])['close']
x_price = data['000001.XSHG'].values
y_price = data['399001.XSHE'].values

计算两个指数一年内的日收益率，记载于 x_pct 和 y_pct 两个 list 中。

x_pct, y_pct = [], []
for i in range(1, len(x_price)):
    x_pct.append(x_price[i]/x_price[i-1]-1)
for i in range(1, len(y_price)):
    y_pct.append(y_price[i]/y_price[i-1]-1)

将数据转化为 array 的形式；不要忘记添加常数项。

x = np.array(x_pct)
X = sm.add_constant(x)
y = np.array(y_pct)

上吧，λu.λv.(sm.OLS(u,v).fit())！全靠你了！

results = sm.OLS(y, X).fit()
print(results.summary())

得到

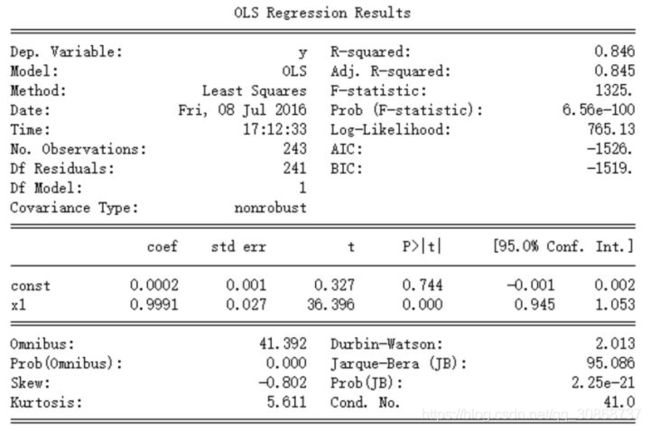
恩，y=0.002+0.9991x，合情合理，或者干脆直接四舍五入到 y=x。最后，画出数据和拟合线。

fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, y, 'o', label="data")
ax.plot(x, results.fittedvalues, 'r--', label="OLS")
ax.legend(loc='best')

全文代码

# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm

#OLS 回归
nsample = 100
#x1 的值从 0 到 10 等差排列
x = np.linspace(0, 10, nsample)
#在 array 上加入一列常项1。
X = sm.add_constant(x)
beta = np.array([1, 10])
e = np.random.normal(size=nsample)
y = np.dot(X, beta) + e
model = sm.OLS(y,X)
results = model.fit()
print(results.params)
print(results.summary())

y_fitted = results.fittedvalues
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, y, 'o', label='data')
ax.plot(x, y_fitted, 'r--.',label='OLS')
ax.legend(loc='best')
ax.axis((-0.05, 2, -1, 25))
plt.show()

#高次模型的回归
nsample = 100
X = np.column_stack((x, x**2))
X = sm.add_constant(X)
beta = np.array([1, 0.1, 10])
e = np.random.normal(size=nsample)
y = np.dot(X, beta) + e
model = sm.OLS(y,X)
results = model.fit()
print(results.params)
print(results.summary())

y_fitted = results.fittedvalues
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, y, 'o', label='data')
ax.plot(x, y_fitted, 'r--.',label='OLS')
ax.legend(loc='best')
ax.axis((-0.05, 2, -1, 25))
plt.show()

#哑变量
nsample = 50
groups = np.zeros(nsample, int)
groups[20:40] = 1
groups[40:] = 2
dummy = sm.categorical(groups, drop=True)
x = np.linspace(0, 20, nsample)
X = np.column_stack((x, dummy))
X = sm.add_constant(X)
beta = [10, 1, 1, 3, 8]
e = np.random.normal(size=nsample)
y = np.dot(X, beta) + e
result = sm.OLS(y,X).fit()
print(result.summary())

fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, y, 'o', label="data")
ax.plot(x, result.fittedvalues, 'r--.', label="OLS")
ax.legend(loc='best')
plt.show()

data = get_price(['000001.XSHG', '399001.XSHE'], start_date='2015-01-01', end_date='2016-01-01', frequency='daily',fields=['close'])['close']
x_price = data['000001.XSHG'].values
y_price = data['399001.XSHE'].values

x_pct, y_pct = [], []
for i in range(1, len(x_price)):
    x_pct.append(x_price[i] / x_price[i - 1] - 1)
for i in range(1, len(y_price)):
    y_pct.append(y_price[i] / y_price[i - 1] - 1)

x = np.array(x_pct)
X = sm.add_constant(x)
y = np.array(y_pct)
results = sm.OLS(y, X).fit()

summary结果中提供了很多关于拟合的信息，下面是这些描述信息的含义：
第一个表左边部分是关于拟合的基本信息:

第一个表的右边部分显示的是拟合的好坏情况：

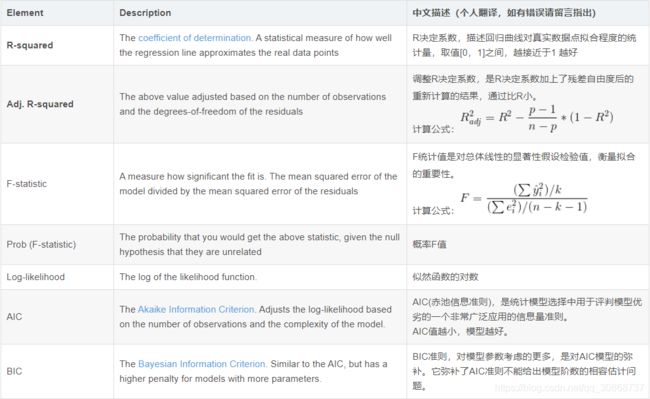
第二个表显示的是拟合系数信息：

最后一个表显示的是对残差分布的统计检验评估：

部分较常用的结果数值提取具体操作示例如下

import statsmodels.api as sm
# 模型训练
model = sm.OLS(y, x).fit()
# 查看模型结果
print(model.summary())

提取元素-回归系数类

# 提取回归系数
model.params

# 提取回归系数标准差
model.bse

# 提取回归系数p值
model.pvalues

# 提取回归系数t值
model.tvalues

# 提取回归系数置信区间 默认5%，括号中可填具体数字 比如0.05, 0.1
model.conf_int()  

# 提取模型预测值
model.fittedvalues

# 提取残差
model.resid

# 模型自由度（系数自由度）
model.df_model

# 残差自由度（样本自由度）
model.df_resid

# 模型样本数量
model.nobs

模型评价类

# 提取R方
model.rsquared

# 提取调整R方
model.rsquared_adj

# 提取AIC
model.aic

# 提取BIC
model.bic

# 提取F-statistic
model.fvalue

# 提取F-statistic 的pvalue
model.f_pvalue

# 模型mse
model.mse_model

# 残差mse
model.mse_resid

# 总体mse
model.mse_total

下面是不太常用的计量经济学方面的系数

# 协方差矩阵比例因子
model.scale

#  White异方差稳健标准误
model.HC0_se

# MacKinnon和White（1985）的异方差稳健标准误
model.HC1_se

#  White异方差矩阵
model.cov_HC0

# MacKinnon和White（1985）的异方差矩阵
model.cov_HC1

参考
https://blog.csdn.net/eylier/article/details/107591731
https://blog.csdn.net/chongminglun/article/details/104242342