参考:梯度下降算法的Python实现
- 批量梯度下降:
for i in range(nb_epochs):
params_grad = evaluate_gradient(loss_function, data, params)
params = params - learning_rate * params_grad
在上述代码中,nb_epochs为迭代次数;data是所有的数据;params_grad是每一个权系数的梯度方向,显然它是一个向量;learning_rate * params_grad 就是权系数要改变的量。
- 随机梯度下降:
for i in range(nb_epochs):
np.random.shuffle(data)
for example in data:
params_grad = evaluate_gradient(loss_function, example, params)
params = params - learning_rate * params_grad
参考上面的代码,data变成了example ,所以BGD变成了SGD。
- 小批量梯度下降:
for i in range(nb_epochs):
np.random.shuffle(data)
for batch in get_batches(data, batch_size=50):
params_grad = evaluate_gradient(loss_function, batch, params)
params = params - learning_rate * params_grad
这次变成了batch,所以就是Mini-batch gradient descent了
import tensorflow as tf
import numpy as np
x = (np.linspace(0, 10, 100))
y_ = x + np.random.normal(0, 1, 100)
x = tf.to_float(np.matrix(x).T)
y_ = tf.to_float(np.matrix(y_).T)
w = tf.Variable(0.000001 + tf.random_normal([1, 100]), name = 'w')
b = tf.Variable(tf.constant([0.000001], dtype= tf.float32), name= 'b')
y = tf.matmul(x, w) + b
loss = tf.reduce_mean(tf.square(y - y_))
train_op = tf.train.GradientDescentOptimizer(0.01).minimize(loss) # vanilla策略(普通的梯度更新策略)
with tf.Session() as sess:
tf.global_variables_initializer().run()
for i in range(20):
sess.run(train_op)
print(sess.run(loss))
64.7117
63.0106
61.3772
59.8085
58.3013
56.853
55.4606
54.1218
52.8338
51.5945
50.4017
49.253
48.1467
47.0807
46.0532
45.0625
44.1069
43.1848
42.2948
41.4355
自适应梯度更新策略
train_Ad = tf.train.AdagradOptimizer(0.7).minimize(loss)
with tf.Session() as sess:
tf.global_variables_initializer().run()
for i in range(20):
sess.run(train_Ad)
print(sess.run(loss))
26.4333
14.6923
9.53683
6.81778
5.21666
4.19792
3.51116
3.0272
2.67413
2.40928
2.20603
2.04696
1.92032
1.81791
1.73391
1.66406
1.60525
1.55513
1.51194
1.47433
动量更新策略
train_mov = tf.train.MomentumOptimizer(0.01, 0.04).minimize(loss)
with tf.Session() as sess:
tf.global_variables_initializer().run()
for i in range(20):
sess.run(train_mov)
print(sess.run(loss))
65.0046
63.2387
61.5431
59.9169
58.3569
56.8599
55.4229
54.043
52.7175
51.4437
50.2192
49.0416
47.9088
46.8186
45.7689
44.7581
43.7841
42.8453
41.9401
41.0669
求导示例
import tensorflow as tf
w1 = tf.Variable([[1,2]])
w2 = tf.Variable([[3,4]])
res = tf.matmul(w1, [[2],[1]])
grads = tf.gradients(res,[w1])
with tf.Session() as sess:
tf.global_variables_initializer().run()
re = sess.run(grads)
print(re)
[array([[2, 1]])]
改进的动量更新策略
(Nesterov Accelerated Gradient, NAG)
(这个算法编写的程序好像有点问题,暂时无法解决)
import numpy as np
import tensorflow as tf
def grads(x):
'''求解损失函数loss的梯度'''
return tf.gradients(loss, x)[0]
x = (np.linspace(0, 10, 100))
y_ = x + np.random.normal(0, 1, 100)
x = tf.to_float(np.matrix(x).T)
y_ = tf.to_float(np.matrix(y_).T)
w = tf.Variable(tf.random_normal([1, 100], seed = 1), name = 'w')
b = tf.Variable(tf.constant([0.000001], dtype= tf.float32), name= 'b')
y = tf.matmul(x, w) + b
loss = tf.reduce_mean(tf.square(y - y_))
def train_op_NAG(lr, mu):
dw, db = tf.gradients(loss, [w, b])
tf.assign(w, w - mu * dw)
tf.assign(b, b - mu * db)
v1 = mu * dw + lr * tf.gradients(loss, w)[0]
v2 = mu * db + lr * tf.gradients(loss, b)[0]
tf.assign(w, w - v1)
tf.assign(b, b - v2)
return w, b
lr = 0.5 # 学习率
mu = 0.1 # 动量系数
with tf.Session() as sess:
tf.global_variables_initializer().run()
for i in range(1000):
sess.run(train_op_NAG(lr, mu))
if i % 100 == 0:
print(sess.run(loss))
86.0236
86.0236
86.0236
86.0236
共轭梯度
import sympy,numpy
import math
import matplotlib.pyplot as pl
from mpl_toolkits.mplot3d import Axes3D as ax3
#共轭梯度法FR、PRP两种格式
def CG_FR(x0,N,E,f,f_d):
X=x0;Y=[];Y_d=[];
n = 1
ee = f_d(x0)
e=(ee[0]**2+ee[1]**2)**0.5
d=-f_d(x0)
Y.append(f(x0)[0,0]);Y_d.append(e)
a=sympy.Symbol('a',real=True)
print('第%2s次迭代:e=%f' % (n, e))
while nE:
n=n+1
g1=f_d(x0)
f1=f(x0+a*f_d(x0))
a0=sympy.solve(sympy.diff(f1[0,0],a,1))
x0=x0-d*a0
X=numpy.c_[X,x0];Y.append(f(x0)[0,0])
ee = f_d(x0)
e = math.pow(math.pow(ee[0,0],2)+math.pow(ee[1,0],2),0.5)
Y_d.append(e)
g2=f_d(x0)
beta=(numpy.dot(g2.T,g2))/numpy.dot(g1.T,g1)
d=-f_d(x0)+beta*d
print('第%2s次迭代:e=%f'%(n,e))
return X,Y,Y_d
def CG_PRP(x0,N,E,f,f_d):
X=x0;Y=[];Y_d=[];
n = 1
ee = f_d(x0)
e=(ee[0]**2+ee[1]**2)**0.5
d=-f_d(x0)
Y.append(f(x0)[0,0]);Y_d.append(e)
a=sympy.Symbol('a',real=True)
print('第%2s次迭代:e=%f' % (n, e))
while nE:
n=n+1
g1=f_d(x0)
f1=f(x0+a*f_d(x0))
a0=sympy.solve(sympy.diff(f1[0,0],a,1))
x0=x0-d*a0
X=numpy.c_[X,x0];Y.append(f(x0)[0,0])
ee = f_d(x0)
e = math.pow(math.pow(ee[0,0],2)+math.pow(ee[1,0],2),0.5)
Y_d.append(e)
g2=f_d(x0)
beta=(numpy.dot(g2.T,g2-g1))/numpy.dot(g1.T,g1)
d=-f_d(x0)+beta*d
print('第%2s次迭代:e=%f'%(n,e))
return X,Y,Y_d
if __name__=='__main__':
'''''
G=numpy.array([[21.0,4.0],[4.0,15.0]])
#G=numpy.array([[21.0,4.0],[4.0,1.0]])
b=numpy.array([[2.0],[3.0]])
c=10.0
x0=numpy.array([[-10.0],[100.0]])
'''
m=4
T=6*numpy.eye(m)
T[0,1]=-1;T[m-1,m-2]=-1
for i in range(1,m-1):
T[i,i+1]=-1
T[i,i-1]=-1
W=numpy.zeros((m**2,m**2))
W[0:m,0:m]=T
W[m**2-m:m**2,m**2-m:m**2]=T
W[0:m,m:2*m]=-numpy.eye(m)
W[m**2-m:m**2,m**2-2*m:m**2-m]=-numpy.eye(m)
for i in range(1,m-1):
W[i*m:(i+1)*m,i*m:(i+1)*m]=T
W[i*m:(i+1)*m,i*m+m:(i+1)*m+m]=-numpy.eye(m)
W[i*m:(i+1)*m,i*m-m:(i+1)*m-m]=-numpy.eye(m)
mm=m**2
mmm=m**3
G=numpy.zeros((mmm,mmm))
G[0:mm,0:mm]=W;G[mmm-mm:mmm,mmm-mm:mmm]=W;
G[0:mm,mm:2*mm]=-numpy.eye(mm)
G[mmm-mm:mmm,mmm-2*mm:mmm-mm]=-numpy.eye(mm)
for i in range(1,m-1):
G[i*mm:(i+1)*mm,i*mm:(i+1)*mm]=W
G[i*mm:(i+1)*mm,i*mm-mm:(i+1)*mm-mm]=-numpy.eye(mm)
G[i*mm:(i+1)*mm,i*mm+mm:(i+1)*mm+mm]=-numpy.eye(mm)
x_goal=numpy.ones((mmm,1))
b=-numpy.dot(G,x_goal)
c=0
f = lambda x: 0.5 * (numpy.dot(numpy.dot(x.T, G), x)) + numpy.dot(b.T, x) + c
f_d = lambda x: numpy.dot(G, x) + b
x0=x_goal+numpy.random.rand(mmm,1)*100
N=100
E=10**(-6)
print('共轭梯度PR')
X1, Y1, Y_d1=CG_FR(x0,N,E,f,f_d)
print('共轭梯度PBR')
X2, Y2, Y_d2=CG_PRP(x0,N,E,f,f_d)
figure1=pl.figure('trend')
n1=len(Y1)
n2=len(Y2)
x1=numpy.arange(1,n1+1)
x2=numpy.arange(1,n2+1)
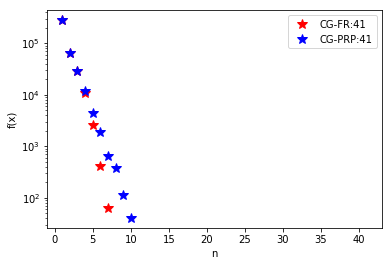
pl.semilogy(x1,Y1,'r*',markersize=10,label='CG-FR:'+str(n1))
pl.semilogy(x2,Y2,'b*',markersize=10,label='CG-PRP:'+str(n2))
pl.legend()
#图像显示了两种种不同的方法各自迭代的次数与最优值变化情况,共轭梯度方法是明显优于最速下降法的
pl.xlabel('n')
pl.ylabel('f(x)')
pl.show()
共轭梯度PR
第 1次迭代:e=258.635139
第 2次迭代:e=139.441695
第 3次迭代:e=19.041089
第 4次迭代:e=41.066524
第 5次迭代:e=8.338590
第 6次迭代:e=6.293510
第 7次迭代:e=4.064956
第 8次迭代:e=2.434763
第 9次迭代:e=0.479482
第10次迭代:e=0.788652
第11次迭代:e=0.361512
第12次迭代:e=0.254609
第13次迭代:e=0.168094
第14次迭代:e=0.144135
第15次迭代:e=0.099708
第16次迭代:e=0.127521
第17次迭代:e=0.078925
第18次迭代:e=0.057012
第19次迭代:e=0.047691
第20次迭代:e=0.003498
第21次迭代:e=0.017225
第22次迭代:e=0.006909
第23次迭代:e=0.005744
第24次迭代:e=0.001183
第25次迭代:e=0.002864
第26次迭代:e=0.001860
第27次迭代:e=0.001019
第28次迭代:e=0.000437
第29次迭代:e=0.000495
第30次迭代:e=0.000158
第31次迭代:e=0.000136
第32次迭代:e=0.000064
第33次迭代:e=0.000062
第34次迭代:e=0.000029
第35次迭代:e=0.000012
第36次迭代:e=0.000012
第37次迭代:e=0.000009
第38次迭代:e=0.000004
第39次迭代:e=0.000002
第40次迭代:e=0.000001
第41次迭代:e=0.000000
共轭梯度PBR
第 1次迭代:e=258.635139
第 2次迭代:e=139.441695
第 3次迭代:e=19.041089
第 4次迭代:e=40.134162
第 5次迭代:e=10.908230
第 6次迭代:e=13.012950
第 7次迭代:e=6.363456
第 8次迭代:e=4.667071
第 9次迭代:e=0.832482
第10次迭代:e=0.639173
第11次迭代:e=1.350706
第12次迭代:e=1.153151
第13次迭代:e=0.576897
第14次迭代:e=0.718519
第15次迭代:e=0.372759
第16次迭代:e=0.220066
第17次迭代:e=0.031159
第18次迭代:e=0.007196
第19次迭代:e=0.056745
第20次迭代:e=0.045436
第21次迭代:e=0.011660
第22次迭代:e=0.006583
第23次迭代:e=0.016376
第24次迭代:e=0.007466
第25次迭代:e=0.001820
第26次迭代:e=0.001621
第27次迭代:e=0.001336
第28次迭代:e=0.001719
第29次迭代:e=0.000987
第30次迭代:e=0.000222
第31次迭代:e=0.000211
第32次迭代:e=0.000038
第33次迭代:e=0.000154
第34次迭代:e=0.000083
第35次迭代:e=0.000033
第36次迭代:e=0.000008
第37次迭代:e=0.000007
第38次迭代:e=0.000004
第39次迭代:e=0.000005
第40次迭代:e=0.000002
第41次迭代:e=0.000000