集成学习-task7&task8

投票法思路

投票法（voting）是集成学习里面针对分类问题的一种结合策略。
基本思想是选择所有机器学习算法当中输出最多的那个类。

分类的机器学习算法输出有两种类型：一种是直接输出类标签，另外一种是输出类概率，使用前者进行投票叫做硬投票(Majority/Hard voting)， 使用后者进行分类叫做软投票(Soft voting)。 sklearn中的VotingClassifier是投票法的实现。

硬投票与软投票实现

硬投票

• 预测结果是所有投票结果最多出现的类。

from sklearn import datasets, linear_model, svm, neighbors
from sklearn.metrics import accuracy_score
from numpy import argmax

# 使用乳腺癌数据
breast_cancer = datasets.load_breast_cancer()
x, y = breast_cancer.data, breast_cancer.target

加载voting模块

from sklearn.ensemble import VotingClassifier
from sklearn import datasets, naive_bayes, svm, neighbors

初始化基础学习器

learner_1 = neighbors.KNeighborsClassifier(n_neighbors=5)  
learner_2 = linear_model.Perceptron(tol=1e-2, random_state=0)
learner_3 = svm.SVC(gamma=0.001)

生成测试集与训练集

test_samples = 150
x_train, y_train = x[:-test_samples], y[:-test_samples]
x_test, y_test = x[-test_samples:], y[-test_samples:]

训练数据

learner_1 = neighbors.KNeighborsClassifier(n_neighbors=5)
learner_2 = linear_model.Perceptron(tol=1e-2, random_state=0)
learner_3 = svm.SVC(gamma=0.001)
voting = VotingClassifier([('KNN', learner_1),
                           ('Prc', learner_2),
                           ('SVM', learner_3)])

拟合与预测

# Fit classifier with the training data
voting.fit(x_train, y_train)

# Predict the most voted class
hard_predictions = voting.predict(x_test)

print('-'*30)
print('Hard Voting:', accuracy_score(y_test, hard_predictions))

------------------------------
Hard Voting: 0.9333333333333333

软投票

• 预测结果是所有投票结果中概率加和最大的类。

# Instantiate the learners (classifiers)
learner_1 = neighbors.KNeighborsClassifier(n_neighbors=5)
learner_2 = naive_bayes.GaussianNB()
learner_3 = svm.SVC(gamma=0.001, probability=True)

# Instantiate the voting classifier
voting = VotingClassifier([('KNN', learner_1),
                           ('NB', learner_2),
                           ('SVM', learner_3)],
                            voting='soft')# 更换投票法方式

voting.fit(x_train, y_train)
learner_1.fit(x_train, y_train)
learner_2.fit(x_train, y_train)
learner_3.fit(x_train, y_train)

SVC(gamma=0.001, probability=True)

# Predict the most probable class
soft_predictions = voting.predict(x_test)

# Get the base learner predictions
predictions_1 = learner_1.predict(x_test)
predictions_2 = learner_2.predict(x_test)
predictions_3 = learner_3.predict(x_test)

# 打印结果
# Accuracies of base learners
print('L1:', accuracy_score(y_test, predictions_1))
print('L2:', accuracy_score(y_test, predictions_2))
print('L3:', accuracy_score(y_test, predictions_3))
# Accuracy of soft voting
print('-'*30)
print('Soft Voting:', accuracy_score(y_test, soft_predictions))

L1: 0.94
L2: 0.96
L3: 0.8933333333333333
------------------------------
Soft Voting: 0.9333333333333333

当投票合集中使用的模型能预测出清晰的类别标签时，适合使用硬投票。当投票集合中使用的模型能预测类别的概率时，适合使用软投票。
软投票同样可以用于那些本身并不预测类成员概率的模型，只要他们可以输出类似于概率的预测分数值（例如支持向量机、k-最近邻和决策树）

投票法的案例分析(基于sklearn，介绍pipe管道的使用以及voting的使用)

pipe管道

• 这个出现了几次了，在这里解决掉

Pipeline可以将许多算法模型串联起来，可以用于把多个estamitors级联成一个estamitor,比如将特征提取、归一化、分类组织在一起形成一个典型的机器学习问题工作流。
Pipleline中最后一个之外的所有estimators都必须是变换器（transformers），最后一个estimator可以是任意类型（transformer，classifier，regresser）,如果最后一个estimator是个分类器，则整个pipeline就可以作为分类器使用，如果最后一个estimator是个聚类器，则整个pipeline就可以作为聚类器使用。

其实就是形成一种工作流，方面简化多个模型调用数据，避免多次预处理数据

from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.ensemble import VotingClassifier
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import RepeatedStratifiedKFold
import numpy as np

models=[('lr',LogisticRegression()),('svm',make_pipeline(StandardScaler(),SVC()))]
ensemble_hard=VotingClassifier(estimators=models,voting='hard')
ensemble_soft=VotingClassifier(estimators=models,voting='soft')

创建样本

from sklearn.datasets import make_classification
def get_dataset():
    X,y=make_classification(n_samples=1000,n_features=20,n_informative=15,
    n_redundant=5,random_state=2)

    return X,y

我们使用多个KNN模型作为基模型演示投票法，其中每个模型采用不同的邻居值K参数

def get_voting():
# define the base 
    modelsmodels = list()
    models.append(('knn1', KNeighborsClassifier(n_neighbors=1)))
    models.append(('knn3', KNeighborsClassifier(n_neighbors=3)))
    models.append(('knn5', KNeighborsClassifier(n_neighbors=5)))
    models.append(('knn7', KNeighborsClassifier(n_neighbors=7)))
    models.append(('knn9', KNeighborsClassifier(n_neighbors=9)))
    # define the voting 
    ensemble_hard = VotingClassifier(estimators=models, voting='hard')
    ensemble_soft = VotingClassifier(estimators=models,voting='soft')
    return ensemble_hard,ensemble_soft

def get_voting():
# define the base 
    modelsmodels = list()
    models.append(('knn1', KNeighborsClassifier(n_neighbors=1)))
    models.append(('knn3', KNeighborsClassifier(n_neighbors=3)))
    models.append(('knn5', KNeighborsClassifier(n_neighbors=5)))
    models.append(('knn7', KNeighborsClassifier(n_neighbors=7)))
    models.append(('knn9', KNeighborsClassifier(n_neighbors=9)))
    # define the voting 
    ensemble = VotingClassifier(estimators=models, voting='hard')
    return ensemble

查看模型提升

def get_models():
    models=dict()
    models['knn1'] = KNeighborsClassifier(n_neighbors=1)
    models['knn3'] = KNeighborsClassifier(n_neighbors=3)
    models['knn5'] = KNeighborsClassifier(n_neighbors=5)
    models['knn7'] = KNeighborsClassifier(n_neighbors=7)
    models['knn9'] = KNeighborsClassifier(n_neighbors=9)
    models['voting']= get_voting()
    return models

evaluate_model()函数接收一个模型实例，并以分层10倍交叉验证三次重复的分数列表的形式返回

from sklearn.model_selection import cross_val_score
def evaluate_model(model,X,y):
    cv=RepeatedStratifiedKFold(n_splits=10,n_repeats=3,random_state=1)
    scores=cross_val_score(model,X,y,scoring='accuracy',cv=cv,n_jobs=-1,error_score='raise')
    return scores

比较算法并可视化

from sklearn.neighbors import KNeighborsClassifier 
from matplotlib import pyplot
X,y=get_dataset()
models=get_models()
results,names=list(),list()
for name,model in models.items():
    scores=evaluate_model(model,X,y)
    results.append(scores)
    names.append(name)
    print('>%s %.3f (%.3f)'% (name, np.mean(scores), np.std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()

>knn1 0.873 (0.030)
>knn3 0.889 (0.038)
>knn5 0.895 (0.031)
>knn7 0.899 (0.035)
>knn9 0.900 (0.033)
>voting 0.910 (0.031)

• 投票法对比其余基模型要好一点，但并没有明显提升

bagging

• Bagging算法：让该学习算法训练多轮，每轮的训练集由从初始的训练集中随机取出的n个训练样本组成，某个初始训练样本在某轮训练集中可以出现多次或根本不出现，训练之后可得到一个预测函数序列h_1，⋯ ⋯h_n ，最终的预测函数H对分类问题采用投票方式，对回归问题采用简单平均方法对新示例进行判别。其本质是对总体进行有放回的抽样！
• 对回归问题的预测是通过预测取平均值来进行的。对于分类问题的预测是通过对预测取多数票预测来进行的。

bagging原理

1. 从原始样本集中用Bootstrap采样选出n个样本(新)

2. 对这n个样本建立分类器

3. 重复1-2步，建立m个分类器

4. 将Bootstrap采样选出n个样本(m个新的样本数据集)，在m个分类器上进行分类

5. 把m个分类器分类的结果进行投票，得到最多的为最终的类别。

Bootstrap原理

Bootstrap采样名字来自成语“pull up by your own bootstraps”，意思是依靠你自己的资源，称为自助法，它是一种有放回的抽样方法，它是非参数统计中一种重要的估计统计量方差进而进行区间估计的统计方法。
其核心思想和基本步骤如下：
1） 采用重抽样技术从原始样本中抽取一定数量（自己给定）的样本，此过程允许重复抽样。

2） 根据抽出的样本计算给定的统计量T。

3） 重复上述N次（一般大于1000），得到N个统计量T。

4） 计算上述N个统计量T的样本方差，得到统计量的方差。

bagging使用前后对比

# 导入算法包以及数据集
from sklearn import neighbors
from sklearn import datasets
from sklearn.ensemble import BaggingClassifier
from sklearn import tree
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')  # 使用自带的样式进行美化
# 下面两行代码用于显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

iris = datasets.load_iris()
x_data = iris.data[:,:2]
y_data = iris.target

x_train,x_test,y_train,y_test = train_test_split(x_data, y_data)
# print(iris)
print(y_data)

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]

没有bagging情况下

def plot(model):
    # 获取数据值所在的范围
    x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
    y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1

    # 生成网格矩阵
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                         np.arange(y_min, y_max, 0.02))

    z = model.predict(np.c_[xx.ravel(), yy.ravel()])# ravel与flatten类似，多维数据转一维。flatten不会改变原始数据，ravel会改变原始数据
    z = z.reshape(xx.shape)
    # 等高线图
    cs = plt.contourf(xx, yy, z)

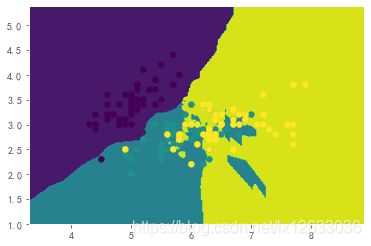
# KNN
knn = neighbors.KNeighborsClassifier()
knn.fit(x_train, y_train)

# 画图
plot(knn)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()
# 准确率
print(knn.score(x_test, y_test))

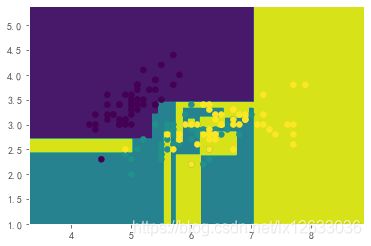
# 决策树
dtree = tree.DecisionTreeClassifier()
dtree.fit(x_train, y_train)
# 画图
plot(dtree)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()
# 准确率
dtree.score(x_test, y_test)

0.6578947368421053

0.6052631578947368

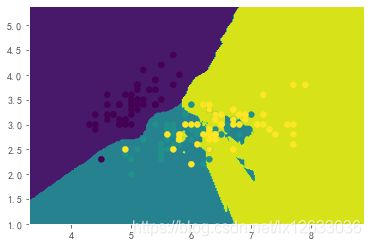
使用bagging

bagging_knn = BaggingClassifier(knn, n_estimators=100)
# 输入数据建立模型
bagging_knn.fit(x_train, y_train)
plot(bagging_knn)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()
print(bagging_knn.score(x_test, y_test))

0.7105263157894737

bagging_tree = BaggingClassifier(dtree, n_estimators=100)
# 输入数据建立模型
bagging_tree.fit(x_train, y_train)
plot(bagging_tree)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()
print(bagging_tree.score(x_test, y_test))

0.6578947368421053

• 可以看出使用bagging后，KNN和决策树都有提升

总结

本次是集成学习的task7，到这里我才真正弄清楚了啥事集成学习。其实就是多个模型进行综合使用，包括之前学习的bagging,stacking，投票法都是属于这个环节。
集成学习的一般结构为：先产生一组“个体学习器”，再用某种策略将它们结合起来。集成中只包含同种类型的个体学习器，称为同质，当中的个体学习器亦称为“基学习器”，相应的算法称为“基学习算法”。集成中包含不同类型的个体学习器，称为“异质”，当中的个体学习器称为“组建学习器”。
通过多个个体学习器组成强学习器，提升准确率。
以下列有一些关于集成学习的参考文献，之后的学习中都可以看看。
相关参考文献：
集成学习(ensemble learning)原理详解
集成学习–bagging、boosting、stacking