TensorFlow应用实战-5- TensorFlow基础知识
从helloworld开始
mkdir 1.helloworld
cd 1.helloworld
vim helloworld.py
代码:
# -*- coding: UTF-8 -*-
# 引入 TensorFlow 库
import tensorflow as tf
# 设置了gpu加速提示信息太多了,设置日志等级屏蔽一些
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='3'
# 创建一个常量 Operation (操作)
hw = tf.constant("Hello World! Mtianyan love TensorFlow!")
# 启动一个 TensorFlow 的 Session (会话)
sess = tf.Session()
# 运行 Graph (计算图)
print (sess.run(hw))
# 关闭 Session(会话)
sess.close()
TensorFlow的编程模式
命令式编程:
- 容易理解,命令语句基本没优化: C,java, C++, Python
符号式编程:
- 涉及较多的嵌入和优化,运行速度有同比提升
计算流图。c和d是可以共用内存的。有一定优化。
# -*- coding: UTF-8 -*-
# 引入 TensorFlow 库
import tensorflow as tf
# 设置了gpu加速提示信息太多了,设置日志等级屏蔽一些
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='3'
a = tf.constant(2)
b = tf.constant(3)
c = tf.multiply(a,b)
d = tf.add(c, 1)
with tf.Session() as sess:
print (sess.run(d))
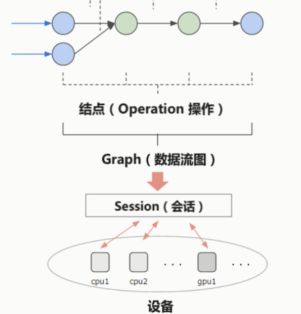
TensorFlow的计算流图,符号式编程的范式。有节点有边,边是计算结果在节点中流动。
TensorFlow的基础结构
Tensor 在 计算流图中流动(flow)
这张图简化一下,取其中一部分。
边就是Tensor(张量)在流动
节点就是一个operation操作,数学计算或后面的激励函数等的操作。
节点的输入与输出都是Tensor张量。
边和节点共同构成了Graph 也就是数据流图。
数据流图会被放进session会话中进行运行。会话可以在不同的设备上去运行,比如cpu和GPU。
图的基本构成
数据流图:
- Tensor (张量) 边里流动的数据
- Operation(操作)
Tensor 会作为operation的输入,operation输出的依然是Tensor
TensorFlow的基础模型
数据模型 - Tensor(张量)
张量是TensorFlow中最重要的结构。
计算模型 - Graph(图)
运行模型 - Session(会话)
图(Graph)与会话(Session)
计算流图,也是TensorFlow的基本架构,表明了图正在运行的状态。
黑色的线不断流动, 其中流动的就是Tensor,一个一个的节点就是它的操作
数据流图的结构
烧杯中进行的化学反应就是操作,其中流动的就是张量。
什么是会话(Session)?
火狐打开一个浏览器就是打开了一个会话。
使用x,y,z三行构建了一个图,构建了一个实验仪器。
TensorFlow使用了客户端和服务端的经典架构。
客户端是我们编写的程序,程序请求服务端(C++)的运行时。
创建一个会话,使用会话中的run方法。
Session的作用
静态的图。数据流图
如何让某一部分动起来?
需要点燃酒精灯。
要让这一部分运行起来。就得run
TensorFlow程序的流程
- 定义算法的计算图(Graph)的结构 静态
- 使用会话(Session) 执行计算
python常用库numpy
TensorFlow和numpy有一定联系
- 有很多类似的概念和api
介绍Tensor时,有很多api名称很相似
numpy官网,科学计算。n阶数组对象。
numpy速度是非常快的,比原生快很多。
因为numpy的许多函数是用c语言来实现的。还使用了一些优化,甚至比你自己用c实现快很多。
scipy 是一个开源软件。Matplotlib。pandas。jupyter notebook
numpy的操作对象是一个多维的数组。类似Tensor
ndarray ndim shape size dtype(同一类型元素)
import numpy as np
vector = np.array([1,2,3])
vector.shape
vector.size
vector.ndim
type(vector)
# 创建二维数组(矩阵)
matrix = np.array([[1, 2],[3, 4]])
matrix.shape
matrix.size
matrix.ndim
type(matrix)
对于矩阵进行转置
one = np.arange(12)
# 0 - 11
one.reshape((3,4))
two = one.reshape((3,4))
two.shape
two.size
two.ndim
什么是Tensor(张量)?
不断流动的东西就是张量。节点就是operation计算
TensorFlow里的数据都是Tensor,所以它可以说是一个张量的流图
张量的维度(秩): Rank / Order dimension
维度是0的话,是一个标量(Scalar)
vector & Matrix
numpy中的基础要素就是array,和Tensor 差不多的一种表述。
import numpy as np
zeros = np.zeros((3,4))
zeros
ones = np.ones((5,6))
ones
# 对角矩阵: 必须是一个方阵.对角线是1,其他都是0的方阵
ident = np.eye(4)
一个张量里面的元素类型都是一样的。
Tensor 的属性
因为一个tensor 只能包含一种数据类型。dtype
TensorFlow.datatype list
https://www.tensorflow.org/api_docs/python/tf/DType
TensorFlow数据类型有很多。
其他属性:
https://www.tensorflow.org/api_docs/python/tf/Tensor
可以通过搜索Tensor 查看到它的其他属性。
A Tensor是一个输出的符号句柄 Operation。它不包含该操作输出的值,而是提供了在TensorFlow中计算这些值的方法tf.Session。
device,在哪个设备上被计算出来的。
Graph 这个Tensor 所属的一个图
name 是我们可以给张量起的名字
op 是产生这个Tensor 的一个操作
几种Tensor
- Constant
- Variable
- Placeholder
- SparseTensor
Constant (常量)
- 值不能改变的一种Tensor
但取这个Tensor值有可能还是会变
定义在tf.constant类
tf.constant(
value,
dtype=None,
shape=None,
name='Const',
verify_shape=False
)
数值:标量,向量,矩阵
verify_shape 验证形状
官网例子:
# Constant 1-D Tensor populated with value list.
tensor = tf.constant([1, 2, 3, 4, 5, 6, 7]) => [1 2 3 4 5 6 7]
# Constant 2-D tensor populated with scalar value -1.
tensor = tf.constant(-1.0, shape=[2, 3]) => [[-1. -1. -1.]
[-1. -1. -1.]]
我们的代码
const = tf.constant(3)
const
# 输出const:0 shape=() dtype=int32
run之后才能得到具体的数。与普通的变量常量是不一样的。
Variable 变量
- 值可以改变的一种tensor
定义在tf.Variable. 注意这个v是大写的,和constant是不一样的。
属性: initial_value
__init__(
initial_value=None,
trainable=True,
collections=None,
validate_shape=True,
caching_device=None,
name=None,
variable_def=None,
dtype=None,
expected_shape=None,
import_scope=None,
constraint=None
)
定义一个变量的张量。
var = tf.Variable(3)
var
# 不会输出真实值,只会输出数据类型等特征量
我们可以在创建变量的时候指定好它的数据类型
var1 = tf.Variable(4, dtype=tf.int64)
var1
# 默认系统给的变量名会自动递增
PlaceHolder(占位符)
- 先占住一个固定的位置,等着你之后往里面添加值的一种Tensor
例子: 图书馆占座
tf.placeholder
https://www.tensorflow.org/api_docs/python/tf/placeholder
tf.placeholder(
dtype,
shape=None,
name=None
)
属性少。没有值。形状。赋值的机制用到了python中字典的机制
x = tf.placeholder(tf.float32, shape=(1024, 1024))
y = tf.matmul(x, x)
with tf.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed.
rand_array = np.random.rand(1024, 1024)
print(sess.run(y, feed_dict={x: rand_array})) # Will succeed.
feed_dict 真正运行时才通过feed_dict关键字以字典形式向里面传值。
SparseTensor(稀疏张量)
- 一种"稀疏"的Tensor,类似线性代数里面的稀疏矩阵的概念
tf.SparseTensor
在矩阵中,若数值为0的元素数目远远多于非0元素的数目,并且非0元素分布没有规律时,则称该矩阵为稀疏矩阵;与之相反,若非0元素数目占大多数时,则称该矩阵为稠密矩阵。 定义非零元素的总数比上矩阵所有元素的总数为矩阵的稠密度。
定义稀疏矩阵,只需要定义非0的数,其他为0的数会自动的填充。
SparseTensor(indices=[[0, 0], [1, 2]], values=[1, 2], dense_shape=[3, 4])
指定坐标,对应坐标的值,以及它的形状。
[[1, 0, 0, 0]
[0, 0, 2, 0]
[0, 0, 0, 0]]
Tensor 表示法
Tensor("MUL:0", shape=(),dtype=float32)
类型 : tf.Variable
名字: MUL
0表示索引
你是operation产生的第几个张量
shape 就是形状 dtype 数据类型
定义一个有名字的Variable
named_var = tf.Variable([5,6], name="named_var")
named_var
自动生成的会以数据类型为名字。
图和会话原理及案例
Graph(图)的形象比喻
每个节点可以想象成一个仪器,在对我们的实验品进行操作。
仪器中被操作,以及在各个仪器中流动的是tensor
TensorFlow程序的流程
- 定义算法的计算图(Graph)结构
把实验的器材等组装好
- 使用会话(Session)执行图的一部分(计算)
开始点燃酒精灯等操作
Graph tf.Graph
https://www.tensorflow.org/api_docs/python/tf/Graph
如果你没有显式的去创建图,它其实已经帮你注册了一个默认的图。
默认Graph总是已注册,并可通过调用访问 tf.get_default_graph。
没有输出值是因为我们还没有用会话运行这一部分。
创建sess对象
我们可以看一下Session这个类
https://www.tensorflow.org/api_docs/python/tf/Session
一个Session对象封装了Operation 执行对象的环境,并对Tensor对象进行评估。例如:
OPeration是图上的节点,输入张量,产生张量。
run(
fetches,
feed_dict=None,
options=None,
run_metadata=None
)
run返回的结果就是一个张量。
>>> tf.get_default_graph()
>>> if c.graph is tf.get_default_graph():
... print("The Graph of c is the default graph")
...
The Graph of c is the default graph
可以看到c所属的图确实是默认图。
程序小例子
# -*- coding: UTF-8 -*-
# 引入tensorflow
import tensorflow as tf
# 设置了gpu加速提示信息太多了,设置日志等级屏蔽一些
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='2'
# 创建两个常量 Tensor.第一个为1行2列,第二个为二行一列。
# 也就是矩阵乘法必须满足,列等于行。
const1 = tf.constant([[2, 2]])
const2 = tf.constant([[4],
[4]])
# 矩阵乘法运算matrix mul tf.add()
multiple = tf.matmul(const1, const2)
# 尝试用print输出multiple的值, 不会输出真实值。因为没运行
print(multiple)
# 创建了 Session (会话) 对象
sess = tf.Session()
# 用Session的run方法来实际运行multiple这个矩阵乘法操作
# 并把操作执行的结果赋值给 result
result = sess.run(multiple)
# 用print打印矩阵乘法的结果
print(result)
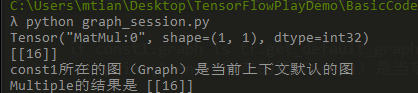
if const1.graph is tf.get_default_graph():
print("const1所在的图(Graph)是当前上下文默认的图")
# 关闭已用完的Session(会话)
sess.close()
# 第二种方法来创建和关闭Session,更安全
with tf.Session() as sess:
result2 = sess.run(multiple)
print("Multiple的结果是 %s " % result2)
用显示的close和with上下文管理器两种方式实现
可视化利器Tensorboard
展示构建的计算图和节点等信息在浏览器里。
人工智能的黑盒
输入手写4等相关4的图片。输出这是4
输入狗狗图片,输出可能是狗狗
输入历史的股票曲线,预测出未来这一年的市值
TensorBoard的作用
打开黑盒,照亮。方便调参等操作。
节点和操作。
上层节点可以打开,看到下层节点。
之后可能会加入debug功能,目前还只是一种展示。
用TensorFlow保存图的信息到日志中
# 第一个参数为指定的保存路径,第二个参数为要保存的图
tf.summary.FileWriter("日志保存路径", sess.graph)
https://www.tensorflow.org/api_docs/python/tf/summary?hl=zh-cn
注意我们这里的summary是小写的summary。
张量摘要用于导出关于模型的信息。
官网的develop 中的get Started 里面有关于TensorBoard的信息。
开源的github源代码。
使用TensorBoard 读取并展示日志
tensorboard --logdir=日志所在路径
Tensorflow安装之后,会默认安装有TensorBoard
Summary(总结,概览)
上一节的代码中自行添加一行
# 第一个参数为指定的保存路径,第二个参数为要保存的图
tf.summary.FileWriter("./", sess.graph)
- 用于导出关于模型的精简信息的方法
- 可以使用TensorBoard等工具访问这些信息
打开浏览器会有一系列菜单。
6006端口打开。
菜单分别是标量,图片,音频,图。
可以点击节点,如果有加号打开节点里面内容。节点含义会列在右边。
distributions 训练的一些分布。histograms 直方图。
对于数字进行分类。
可以分类进行颜色加颜色。
namespace(命名空间)
我们刚才点击过的双击图形,节点里面又有子节点。
- 很像一些编程语言(如 c++) 的namespace, 包含嵌套的关系
卷积神经网络下的偏差,adam方法(一种优化方法)
符号的含义
一般的操作不会改变输入的Tensor,如果是一条黄线,表示操作节点可以改变输入的Tensor
使用TensorBoard展示图代码示例
# -*- coding: UTF-8 -*-
# 引入tensorflow
import tensorflow as tf
# 设置了gpu加速提示信息太多了,设置日志等级屏蔽一些
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='3'
# 构造图(Graph)的结构
# 用一个线性方程的例子 y = W * x + b
# 梯度下降法求w和b
W = tf.Variable(2.0, dtype=tf.float32, name="Weight") # 权重
b = tf.Variable(1.0, dtype=tf.float32, name="Bias") # 偏差
x = tf.placeholder(dtype=tf.float32, name="Input") # 输入
with tf.name_scope("Output"): # 输出的命名空间
y = W * x + b # 输出
#const = tf.constant(2.0) # 常量,不需要初始化
# 定义保存日志的路径
path = "./log"
# 创建用于初始化所有变量 (Variable) 的操作
init = tf.global_variables_initializer()
# 创建Session(会话)
with tf.Session() as sess:
sess.run(init) # 初始化变量
# 写入日志文件
writer = tf.summary.FileWriter(path, sess.graph)
# 因为x是一个placeholder,需要进行值的填充
result = sess.run(y, {x: 3.0})
print("y = %s" % result) # 打印 y = W * x + b 的值,就是 7
使用tensorBoard
tensorboard --logdir=./log
6006类似于GOOGle的goog
不像之前的例子有很多菜单,只打开了一个graph菜单。
之后的图有可能很复杂,查看损失函数,优化计算流图。
酷炫模拟游乐场playground
生活中所见的游乐园。
展示了基本的神经网络结构
- JavaScript编写的网页应用
- 通过浏览器就可以训练简单的神经网络
- 训练过程可视化,高度定制化
https://playground.tensorflow.org/
不用担心运行复杂的神经网络而搞垮。
数据集 - 特征 - 隐藏层(深度: 很多层) - 输出
测试的损失。训练的损失。越接近0越好。
epoch是完整的运行过程。
黄色越黄越接近-1
点亮输入。选择激励函数。问题类型分类还是回归。
游乐场对神经网络有更形象的认识。
常用的python绘图库Matplotlib
一个极其强大的python绘图库:
https://matplotlib.org/
官网有很多例子。
scipy下的一个组件。
很少的代码即可绘制2d 3d 静态动态等各种图形
一般常用的是它的子包: pyplot 提供类似matlab的绘图框架
Matplotlib的一般绘图流程
sudo pip install matplotlib
代码:
# -*- coding: UTF-8 -*-
# 引入 Matplotlib 的分模块 pyplot
import matplotlib.pyplot as plt
# 引入 numpy
import numpy as np
# 创建数据
# Linespace创建一定范围内的图线。-2到2之间等分100个点
x = np.linspace(-2, 2, 100)
#y = 3 * x + 4
y1 = 3 * x + 4
y2 = x ** 3
# 创建图像
#plt.plot(x, y)
plt.plot(x, y1)
plt.plot(x, y2)
# 显示图像
plt.show()
蓝色的为y1.从-2到2的一条直线。
代码示例2:
# -*- coding: UTF-8 -*-
import matplotlib.pyplot as plt
import numpy as np
# 创建数据
x = np.linspace(-4, 4, 50)
y1 = 3 * x + 2
y2 = x ** 2
# 第一张图
# 指定图的大小
plt.figure(num=1, figsize=(7, 6))
# 第一张图两个线
plt.plot(x, y1)
plt.plot(x, y2, color="red", linewidth=3.0, linestyle="--")
# 第二张图
plt.figure(num=2)
plt.plot(x, y2, color="green")
# 显示所有图像
plt.show()
代码示例3:
子图的绘制
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import NullFormatter # useful for `logit` scale
# Fixing random state for reproducibility
# 为了重现结果,设置随机种子
np.random.seed(19680801)
# make up some data in the interval ]0, 1[
y = np.random.normal(loc=0.5, scale=0.4, size=1000)
y = y[(y > 0) & (y < 1)]
y.sort()
x = np.arange(len(y))
# plot with various axes scales
plt.figure(1)
# linear
# 两行两列子图中第一个
plt.subplot(221)
plt.plot(x, y)
plt.yscale('linear')
plt.title('linear')
plt.grid(True)
# log
plt.subplot(222)
plt.plot(x, y)
plt.yscale('log')
plt.title('log')
plt.grid(True)
# symmetric log
plt.subplot(223)
plt.plot(x, y - y.mean())
plt.yscale('symlog', linthreshy=0.01)
plt.title('symlog')
plt.grid(True)
# logit
plt.subplot(224)
plt.plot(x, y)
plt.yscale('logit')
plt.title('logit')
plt.grid(True)
# Format the minor tick labels of the y-axis into empty strings with
# `NullFormatter`, to avoid cumbering the axis with too many labels.
plt.gca().yaxis.set_minor_formatter(NullFormatter())
# Adjust the subplot layout, because the logit one may take more space
# than usual, due to y-tick labels like "1 - 10^{-3}"
plt.subplots_adjust(top=0.92, bottom=0.08, left=0.10, right=0.95, hspace=0.25,
wspace=0.35)
plt.show()
绘制一个像碗一样的图像。
from mpl_toolkits.mplot3d.axes3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
fig, ax1 = plt.subplots(figsize=(8, 5),
subplot_kw={'projection': '3d'})
alpha = 0.8
r = np.linspace(-alpha,alpha,100)
X,Y= np.meshgrid(r,r)
l = 1./(1+np.exp(-(X**2+Y**2)))
ax1.plot_wireframe(X,Y,l)
ax1.plot_surface(X,Y,l, cmap=plt.get_cmap("rainbow"))
ax1.set_title("Bowl shape")
plt.show()
制作静态图像,制作动态图像。
示例5:
import numpy as np
from matplotlib import cm
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d.axes3d as p3
import matplotlib.animation as animation
def cost_function(x):
return x[0]**2 + x[1]**2
def gradient_cost_function(x):
return np.array([2*x[0], 2*x[1]])
nb_steps = 20
x0 = np.array([0.8, 0.8])
learning_rate = 0.1
def gen_line():
x = x0.copy()
data = np.empty((3, nb_steps+1))
data[:, 0] = np.concatenate((x, [cost_function(x)]))
for t in range(1, nb_steps+1):
grad = gradient_cost_function(x)
x -= learning_rate * grad
data[:, t] = np.concatenate((x, [cost_function(x)]))
return data
def update_line(num, data, line):
# NOTE: there is no .set_data() for 3 dim data...
line.set_data(data[:2, :num])
line.set_3d_properties(data[2, :num])
return line
# Attaching 3D axis to the figure
fig = plt.figure()
ax = p3.Axes3D(fig)
# Plot cost surface
X = np.arange(-0.5, 1, 0.1)
Y = np.arange(-1, 1, 0.1)
X, Y = np.meshgrid(X, Y)
Z = cost_function((X, Y))
surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm, linewidth=0, antialiased=False)
# Optimize
data = gen_line()
# Creating line objects
# NOTE: Can't pass empty arrays into 3d version of plot()
line = ax.plot(data[0, 0:1], data[0, 0:1], data[0, 0:1], 'rx-', linewidth=2)[0]
# Setting the axes properties
ax.view_init(30, -160)
ax.set_xlim3d([-1.0, 1.0])
ax.set_xlabel('X')
ax.set_ylim3d([-1.0, 1.0])
ax.set_ylabel('Y')
ax.set_zlim3d([0.0, 2.0])
ax.set_zlabel('Z')
# Creating the Animation object
line_ani = animation.FuncAnimation(fig, update_line, nb_steps+1, fargs=(data, line), \
interval=200, blit=False)
# line_ani.save('gradient_descent.gif', dpi=80, writer='imagemagick')
plt.show()
演示了梯度下降的示例
tensorflow-mnist-tutorial的代码示例
代码下载地址:
https://github.com/martin-gorner/tensorflow-mnist-tutorial
注意错误:
ImportError: No module named 'tensorflowvisu'
是因为这个tensorflowvisu.py的文件得位于同一级目录。
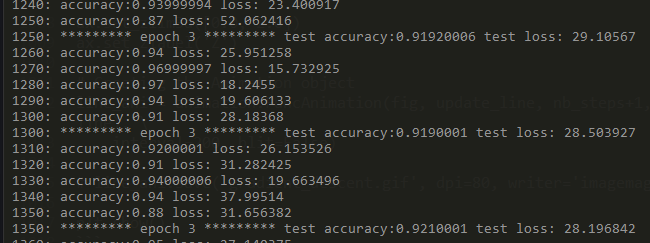
可以看到精度在不断上升。损失在不断降低。可以看到他训练了哪些数字。
weights,权重。Biases,偏差。 测试的手写数字
这个例子是用TensorFlow结合Matplotlib来绘制一个实时的动图。
综合小练习:梯度下降解决线性回归
线性回归一般用于预测,比如: 股票涨跌
梯度下降是机器学习中最核心的优化算法
复习一下Operation(操作)
- 基本的操作:
- 逐元素的数学操作
- 矩阵操作
- 状态型操作
- 神经网络操作
- 保存,还原操作
- 模型训练操作
tf.nn.relu
tf.add
这些都可以在官网直接搜索查看到。
一些等价的操作
查看在线文档,搜索,或目录查看。
help(要查看的对象)
梯度下降优化器
构建一个基于梯度下降的优化器。
# -*- coding: UTF-8 -*-
'''
用梯度下降的优化方法来快速解决线性回归问题
'''
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
# 构建数据:100个随机点
points_num = 100
# 之后要往vectors中填充100个点的值
vectors = []
# 用 Numpy 的正态随机分布函数生成 100 个点
# 这些点的(x, y)坐标值: 对应线性方程 y = 0.1 * x + 0.2
# 权重 (Weight) 为 0.1,偏差 (Bias)为 0.2
try:
# 运行100次
for i in xrange(points_num):
# 横坐标值,随机正态分布函数。区间0-0.66
x1 = np.random.normal(0.0, 0.66)
# 在真实值上加一些偏差
y1 = 0.1 * x1 + 0.2 + np.random.normal(0.0, 0.04)
# 将点list加入vectors列表中
vectors.append([x1, y1])
except:
for i in range(points_num):
x1 = np.random.normal(0.0, 0.66)
y1 = 0.1 * x1 + 0.2 + np.random.normal(0.0, 0.04)
vectors.append([x1, y1])
x_data = [v[0] for v in vectors] # 列表生成式取出真实的点的 x 坐标
y_data = [v[1] for v in vectors] # 真实的点的 y 坐标
# 图像 1 :展示 100 个随机数据点
plt.plot(x_data, y_data, 'ro', label="Original data") # 红色圆圈圈型的点
plt.title("Linear Regression using Gradient Descent")
# 展示label
plt.legend()
plt.show()
我们要找到一条线性回归的直线,之后给它x值就可以预测y值。也就是寻找一条直线它的w最接近0.1,b最接近于0.2最好。
构建线性回归模型
# 构建线性回归模型
# 初始化参数,传入shape,最小值,最大值
W = tf.Variable(tf.random_uniform([1], -1.0, 1.0)) # 初始化 Weight
# 偏差。初始化为0
b = tf.Variable(tf.zeros([1])) # 初始化 Bias
# 这里的y是y帽子,也就是模型预测出来的值
y = W * x_data + b # 模型计算出来的 y
# 定义 loss function (损失函数) 或 cost function (代价函数)
# 计算残差平方和。用(y帽子-真实的y)的平方累加的和。N就是总的点数,100.
# 对 Tensor 的所有维度计算 ((y - y_data) ^ 2) 之和 / N
# reduce_mean就是最后面的/N操作。square平方: y - y_data
loss = tf.reduce_mean(tf.square(y - y_data))
# 用梯度下降的优化器来优化我们的 loss functioin
# 让它更快的找到最终最拟合的w和b: 梯度下降的优化器。学习率,梯度下降的快慢。
optimizer = tf.train.GradientDescentOptimizer(0.5) # 设置学习率为 0.5(步长),一般都是小于1的数。
# 太大的学习率可能错过局部最小值的那个点。
# 让它(损失函数)尽可能的损失最小
train = optimizer.minimize(loss)
# 创建会话
sess = tf.Session()
# 初始化数据流图中的所有变量
init = tf.global_variables_initializer()
sess.run(init)
try:
# 训练 20 步
for step in range(20):
# 优化每一步
sess.run(train)
# 打印出每一步的损失,权重和偏差.必须run才能得到实际的值。
print(("Step=%d, Loss=%f, [Weight=%f Bias=%f]") % (step, sess.run(loss), sess.run(W), sess.run(b)))
except:
# 训练 20 步
for step in xrange(20):
# 优化每一步
sess.run(train)
# 打印出每一步的损失,权重和偏差
print("Step=%d, Loss=%f, [Weight=%f Bias=%f]") \
% (step, sess.run(loss), sess.run(W), sess.run(b))
# 图像 2 :绘制所有的点并且绘制出最佳拟合的直线
plt.plot(x_data, y_data, 'bo', label="Original data") # 蓝色圆圈的点
plt.title("Linear Regression using Gradient Descent")
# 横坐标是x_data.纵坐标为此时的wb确定的y
plt.plot(x_data, sess.run(W) * x_data + sess.run(b), label="Fitted line") # 拟合的线
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.show()
# 关闭会话
sess.close()
进阶版模仿:
做出拟合过程的动态图像。
激活函数
主要作用: 加入非线性
tf.nn 点击nn
https://www.tensorflow.org/api_guides/python/nn#Activation_Functions
可以看到供我们使用的激活函数。
wiki中不同激活函数的图像,变种。
https://en.wikipedia.org/wiki/Activation_function
1 / float(1 + np.exp(-x))
# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
# 创建输入数据
x = np.linspace(-7, 7, 180) # (-7, 7) 之间等间隔的 180 个点
# 激活函数的原始手工实现
def sigmoid(inputs):
# y = 1 / (1 + exp(-x)) np.exp相当于e的多少次方
y = [1 / float(1 + np.exp(-x)) for x in inputs]
return y
def relu(inputs):
# f(x) = max(0,x) x大于0时,函数值y就是x。x<0时函数值y就是0.
# x如果大于0,则真值为1;y=x;而x若不满足>0真值为0;y=0
y = [x * (x > 0) for x in inputs]
return y
def tanh(inputs):
# e的x次方-e的负x次方做分母。e的x次方+e的负x次方做分母
y = [(np.exp(x) - np.exp(-x)) / float(np.exp(x) - np.exp(-x)) for x in inputs]
return y
def softplus(inputs):
# y = log(1+e的x平方)
y = [np.log(1 + np.exp(x)) for x in inputs]
return y
# 经过 TensorFlow 的激活函数处理的各个 Y 值
y_sigmoid = tf.nn.sigmoid(x)
y_relu = tf.nn.relu(x)
y_tanh = tf.nn.tanh(x)
y_softplus = tf.nn.softplus(x)
# 创建会话
sess = tf.Session()
# 运行run,得到四个返回值
y_sigmoid, y_relu, y_tanh, y_softplus = sess.run([y_sigmoid, y_relu, y_tanh, y_softplus])
# 创建各个激活函数的图像
plt.figure(1, figsize=(8, 6))
plt.subplot(221)
plt.plot(x, y_sigmoid, c='red', label='Sigmoid')
# y轴取值的区间
plt.ylim((-0.2, 1.2))
# 显示label,放在最适合的位置
plt.legend(loc='best')
plt.subplot(222)
plt.plot(x, y_relu, c='red', label='Relu')
plt.ylim((-1, 6))
plt.legend(loc='best')
plt.subplot(223)
plt.plot(x, y_tanh, c='red', label='Tanh')
plt.ylim((-1.3, 1.3))
plt.legend(loc='best')
plt.subplot(224)
plt.plot(x, y_softplus, c='red', label='Softplus')
plt.ylim((-1, 6))
plt.legend(loc='best')
# 显示图像
plt.show()
# 关闭会话
sess.close()
动手实现cnn卷积神经网络
用到的数据集: MNIST(手写数字的数据库)
TensorFlow中封装了这个数据集。
我们要构建的cnn的结构大致如上图所示
输入时
28*28*1的一张图片。黑白图片所以高度为1,如果是彩色的,高度为3.红绿蓝。
第一层卷积,有32个过滤器。会变成一个28*28*32的矩阵
经过池化层的Pool(2*2)会变成14*14*32的网络结构
第二层卷积,有64个过滤器。会变成14*14*64的结构
在经过一个Pool 亚采样层,就会变成一个7*7*64
之后再进行扁平的序化。就变成1*1*1024
最后经过一个全连接网络去输出。输出1*1*10
下载数据并声明变量
# -*- coding: UTF-8 -*-
import numpy as np
import tensorflow as tf
# 下载并载入 MNIST 手写数字库(55000 * 28 * 28)55000 张训练图像
from tensorflow.examples.tutorials.mnist import input_data
# 这个名字是自定义的,会保存在当前目录下。如果已经下载的有了,下次就不会download了。
mnist = input_data.read_data_sets('mnist_data', one_hot=True)
# one_hot 独热码的编码 (encoding) 形式
# 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 的十位数字
# 第一位上被激活,唯一的表示这一个数字。
# 0 : 1000000000
# 1 : 0100000000
# 2 : 0010000000
# 3 : 0001000000
# 4 : 0000100000
# 5 : 0000010000
# 6 : 0000001000
# 7 : 0000000100
# 8 : 0000000010
# 9 : 0000000001
# onehot设置True会表示成onehot的编码。否则会表示本身。
# None 表示张量 (Tensor) 的第一个维度可以是任何长度 除以255
input_x = tf.placeholder(tf.float32, [None, 28 * 28]) / 255. # 输入
output_y = tf.placeholder(tf.int32, [None, 10]) # 输出:10个数字的标签
input_x_images = tf.reshape(input_x, [-1, 28, 28, 1]) # 改变形状之后的输入
理清卷积神经网络的原理和思路
我们想去构建的是一个类似于上图的结构的卷积神经网络。
输入是一张28,28,1的灰度图,1表示它只有一个颜色。
图片经过层层的卷积与池化之后会有一个输出。会变成一个1,1,10的输出
我们想要通过图片数据+标签 通过cnn 预测出0-9十种结果。
我们的CNN识别mnist的输入端是这样的。
28,28像素的一个图片。784
而mnist中的图片张数是55000张图片。
输出是如上图,对应了55000维度,对于每一个预测的值它有一个onehot的编码
只有一位取1,其他位全部为0.
表示识别出来的数字分别为4,9,5,8
padding决定补零模式。same表示输入与输出的维数一致。
# 从 Test(测试)数据集里选取 3000 个手写数字的图片和对应标签
test_x = mnist.test.images[:3000] # 图片
test_y = mnist.test.labels[:3000] # 标签
# 构建我们的卷积神经网络:
# 第 1 层卷积(二维的卷积) tf.nn 和 tf.layers 中的cov2d有相似有不同。
# 让图像经过卷积层,维度变为28*28*32。用一个5,5的过滤器(采集器)。
# 从左上角到右下角一点一点采集。每个过滤器扫一遍,输出增加一层。
# 扫了32遍,深度就会从1变为32
# 第二个卷积层,扫了64遍,变成了64
# tf.layers.conv2d二维的卷积函数(https://www.tensorflow.org/api_docs/python/tf/layers/conv2d?hl=zh-cn)
conv1 = tf.layers.conv2d(
inputs=input_x_images, # 形状 [28, 28, 1],这里还是一个placeholder,后面会填充值
filters=32, # 32 个过滤器,输出的深度(depth)是32
kernel_size=[5, 5], # 过滤器(卷积核心)在二维的大小是(5 * 5)
strides=1, # 卷积步幅,步长是1
padding='same', # same 表示输出的大小不变,因此需要在外围补零 2 圈
activation=tf.nn.relu # 激活函数是 Relu
) # 形状 [28, 28, 32]
池化(亚采样)
# 第 1 层池化(亚采样)比原来的那些数据,输出没有输入那么多、
# 只采一部分数据。
pool1 = tf.layers.max_pooling2d(
inputs=conv1, # 形状 [28, 28, 32]
pool_size=[2, 2], # 过滤器在二维的大小是(2 * 2)
strides=2 # 步长是 2
) # 经过亚采样之后,形状 [14, 14, 32]
pooling有几种方案。平均,max。平面区域中选最大的值。
输入必须是一个张量,要有四个维度
https://www.tensorflow.org/api_docs/python/tf/layers/max_pooling2d?hl=zh-cn
步长为2,隔一步采一个样。
亚采样层的过滤器只有一个,所以没有改变深度。改变了二维大小
构建第二层卷积
经过卷积层,深度会不断加深。提取到的特征会不断增多。
# 第 2 层卷积
conv2 = tf.layers.conv2d(
inputs=pool1, # 输入形状 [14, 14, 32]
filters=64, # 64 个过滤器,输出的深度(depth)是64
kernel_size=[5, 5], # 过滤器在二维的大小是(5 * 5)
strides=1, # 步长是1
padding='same', # same 表示输出的大小不变,因此需要在外围补零 2 圈
activation=tf.nn.relu # 激活函数是 Relu
) # 输出形状 [14, 14, 64]
构建第二层池化
第二层池化的过滤器是绿色方块。
# 第 2 层池化(亚采样)
pool2 = tf.layers.max_pooling2d(
inputs=conv2, # 形状 [14, 14, 64]
pool_size=[2, 2], # 过滤器在二维的大小是(2 * 2)
strides=2 # 步长是 2
) # 输出形状 [7, 7, 64]
知道原理之后,构建神经网络就跟做三明治汉堡包似的,来层面包来片肉。
flat平坦化
将输出的7,7,64 压成1,1,1024
# 平坦化(flat)
flat = tf.reshape(pool2, [-1, 7 * 7 * 64]) # 形状 会变成[7 * 7 * 64, ]
输入时pool2。-1表示: 根据之后确定的参数推断-1这个位置的参数大小。
扁平化。将三维形状,扁平化。
全连接层
# 1024 个神经元的全连接层
dense = tf.layers.dense(inputs=flat, units=1024, activation=tf.nn.relu)
有多少个神经元组成的全连接层。全连接层也有一个激活函数的参数,如果没有加激活函数,会是一个线性的,加了激活函数会变成一个非线性的。这里我们拥有一个有1024神经元的全连接层
Dropout
丢弃50% rate(丢弃的率)是0.5
# Dropout : 丢弃 50%, rate=0.5
dropout = tf.layers.dropout(inputs=dense, rate=0.5)
再经过一个10个神经元的全连接层,也就是真实的输出了。
# 10 个神经元的全连接层,这里不用激活函数来做非线性化了
logits = tf.layers.dense(inputs=dropout, units=10) # 输出。形状[1, 1, 10]
计算误差
# 计算误差 (计算 Cross entropy (交叉熵),再用 Softmax 计算百分比概率)
loss = tf.losses.softmax_cross_entropy(onehot_labels=output_y, logits=logits)
https://www.tensorflow.org/api_docs/python/tf/losses/softmax_cross_entropy
交叉熵的损失。
onehot_labels 就是我们真实的标签值,output_y,暂时是一个placeholder,之后会赋值(训练集里对应的真实标签)。
logits 传入我们的预估,logits(y帽子)
用Adam 优化器来最小化误差,学习率 0.001
# Adam 优化器来最小化误差,学习率 0.001使之最小化。使loss最小
train_op = tf.train.AdamOptimizer(learning_rate=0.001).minimize(loss)
精度,计算预测值 和 实际标签的匹配程度
# 精度。计算 预测值 和 实际标签 的匹配程度
# 返回(accuracy, update_op), 会创建两个局部变量
accuracy = tf.metrics.accuracy(
labels=tf.argmax(output_y, axis=1),
predictions=tf.argmax(logits, axis=1),)[1]
https://www.tensorflow.org/api_docs/python/tf/metrics/accuracy
Calculates how often predictions matches labels
计算预测值与真实值之间的差距,匹配度
argmax函数会返回张量轴上最大值的下标。
accuracy函数会返回两个值,我们取其中一个值。
accuracy:Tensor代表准确度,total除以的值count。
update_op:一种适当增加total和count变量并且其值匹配的操作accuracy。
训练神经网络
# 创建会话
sess = tf.Session()
# 初始化变量:全局和局部
init = tf.group(tf.global_variables_initializer(), tf.local_variables_initializer())
sess.run(init)
初始化全局和局部变量。group是一个组的概念。
https://www.tensorflow.org/api_docs/python/tf/group
创建一个将多个操作分组的操作。
训练我们的神经网络
# 训练神经网络
for i in range(20000):
# 从训练集中进行选取。batch,一包。
batch = mnist.train.next_batch(50) # 从 Train(训练)数据集里取"下一个"50 个样本
# run之后,loss的返回值给到train_loss train_op的值给到train_op_
# 给实际的input_x和input_y赋值。batch有两列,0是图片,1是真实标签。
train_loss, train_op_ = sess.run([loss, train_op], {input_x: batch[0], output_y: batch[1]})
if i % 100 == 0:
# 这里测试的精度是在测试集上的精度。
test_accuracy = sess.run(accuracy, {input_x: test_x, output_y: test_y})
# 步数,训练的损失,测试的精度
print(("Step=%d, Train loss=%.4f, [Test accuracy=%.2f]") \
% (i, train_loss, test_accuracy))
测试,打印20个预测值和真实值的对
# 测试:打印 20 个预测值 和 真实值 的对
# 输入测试集的20项,输出预测的y(onehot)
test_output = sess.run(logits, {input_x: test_x[:20]})
# 取到它预测的y是哪个真实数字
inferenced_y = np.argmax(test_output, 1)
print(inferenced_y, 'Inferenced numbers') # 推测的数字
# 取出测试集中的真实标签值
print(np.argmax(test_y[:20], 1), 'Real numbers') # 真实的数字