现在我们知道了如何更新我们的权重:
Δwij=ηδjxi,
你看到的是如何实现一次更新,那我们如何把代码转化为能够计算多次权重更新,使得我们的网络能够真正学习呢?
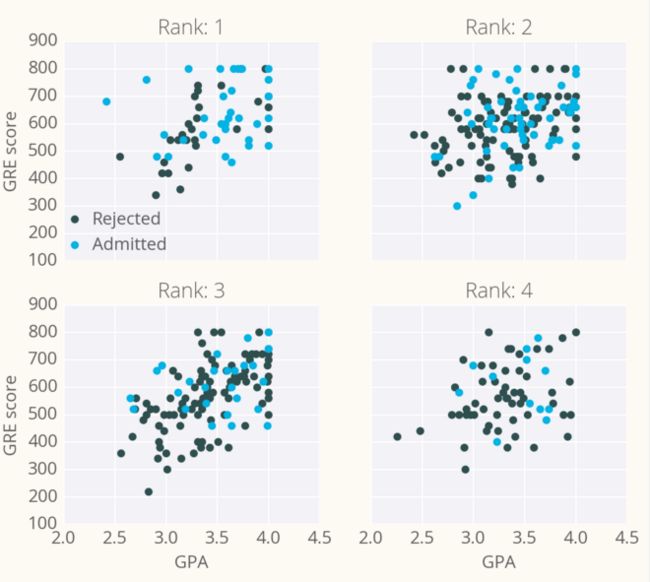
作为示例,我们拿一个研究生学院录取数据,用梯度下降训练一个网络。数据可以在这里找到。数据有三个输入特征:GRE 分数、GPA 分数和本科院校排名(从 1 到 4)。排名 1 代表最好,排名 4 代表最差。
我们的目标是基于这些特征来预测一个学生能否被研究生院录取。这里,我们将使用有一个输出层的网络。用 sigmoid 做为激活函数。
数据清理
你也许认为有三个输入单元,但实际上我们要先做数据转换。rank是类别特征,其中的数字并不表示任何相对的值。排名第 2 并不是排名第 1 的两倍;排名第 3 也不是排名第 2 的 1.5 倍。因此,我们需要用 dummy variables 来对 rank 进行编码。把数据分成 4 个新列,用 0 或 1 表示。排名为 1 的行对应 rank_1 列的值为 1 ,其余三列的值为 0;排名为 2 的行对应 rank_2 列的值为 1 ,其余三列的值为 0,以此类推。
我们还需要把 GRE 和 GPA 数据标准化,也就是说使得它们的均值为 0,标准偏差为 1。因为 sigmoid 函数会挤压很大或者很小的输入,所以这一步是必要的。很大或者很小输入的梯度为 0,这意味着梯度下降的步长也会是 0。由于 GRE 和 GPA 的值都相当大,我们在初始化权重的时候需要非常小心,否则梯度下降步长将会消失,网络也没法训练了。相对地,如果我们对数据做了标准化处理,就能更容易地对权重进行初始化。
这只是一个简单介绍,你之后还会学到如何预处理数据,如果你想了解我是怎么做的,可以查看下面编程练习中的 data_prep.py文件。
经过转换后的 10 行数据
现在数据已经准备好了,我们看到有六个输入特征:gre、gpa,以及四个 rank的虚拟变量 (dummy variables)。
均方差
这里我们要对如何计算误差做一点小改变。我们不计算 SSE,而是用误差平方的均值(mean of the square errors,MSE)。现在我们要处理很多数据,把所有权重更新加起来会导致很大的更新,使得梯度下降无法收敛。为了避免这种情况,你需要一个很小的学习率。这里我们还可以除以数据点的数量 m 来取平均。这样,无论我们有多少数据,我们的学习率通常会在 0.01 to 0.001 之间。我们用 MSE(下图)来计算梯度,结果跟之前一样,只是取了平均而不是取和。
- 这是用梯度下降来更新权重的算法概述:
权重步长设定为 0: Δwi=0
对训练数据中的每一条记录:通过网络做正向传播,计算输出 y^=f(∑iwixi)
计算输出单元的误差项(error term) δ=(y−y^)∗f′(∑iwixi)
更新权重步长 Δwi=Δwi+δxi
更新权重 wi=wi+ηΔwi/m。其中 η 是学习率, m 是数据点个数。这里我们对权重步长做了平均,为的是降低训练数据中大的变化。
重复 e 代(epoch)。你也可以对每条记录更新权重,而不是把所有记录都训练过之后再取平均。
这里我们还是使用 sigmoid 作为激活函数
f(h)=1/(1+e−h)
sigmoid 的梯度是: f′(h)=f(h)(1−f(h))
其中 h 是输出单元的输入
h=∑iwixi
用 NumPy 来实现
这里大部分都可以用 NumPy 很方便的实现。
首先你需要初始化权重。我们希望它们比较小,这样输入在 sigmoid 函数那里可以在接近 0 的位置,而不是最高或者最低处。很重要的一点是要随机地初始化它们,这样它们有不同的初始值,是发散且不对称的。所以我们用一个中心为 0 的正态分布来初始化权重,此正态分布的标准差(scale 参数)最好使用 1/√n,其中 n 是输入单元的个数。这样就算是输入单元的数量变多,sigmoid 的输入还能保持比较小。
weights = np.random.normal(scale=1/n_features**.5, size=n_features)
NumPy 提供了一个可以让两个数组做点乘的函数,它可以让我们方便地计算 h。点乘就是把两个数组的元素对应位置相乘之后再相加。
# input to the output layer
# 输出层的输入output_in = np.dot(weights, inputs)
最后我们可以用 weights += ...更新 Δwi 和 wi,weights += ...是 weights = weights + ...的简写。
效率提示
因为这里我们用的是 sigmoid 函数,你可以节省一些计算。对于 sigmoid 函数来说,f′(h)=f(h)(1−f(h))。也就是说一旦你有了 f(h),你就可以直接用它的值来计算误差的梯度了。
编程练习
接下来,你要实现一个梯度下降,用录取数据来训练它。你的目标是训练一个网络直到你达到训练数据的最小的均方差 mean square error (MSE)。你需要实现:
网络的输出: output
输出误差: error
误差项: error_term
权重步长更新: del_w +=
权重更新: weights +=
在你写完这几部分之后,点击“测试答案”按钮来进行训练,均方差会被打印出来,同时也会打印出测试集的准确率,即录取情况的正确预测比率。
你可以任意调节超参数 hyperparameters 来看下它对均方差 MSE 有什么影响。
import numpy as np
from data_prep import features, targets, features_test, targets_test
def sigmoid(x):
"""
Calculate sigmoid
"""
return 1 / (1 + np.exp(-x))
# TODO: We haven't provided the sigmoid_prime function like we did in
# the previous lesson to encourage you to come up with a more
# efficient solution. If you need a hint, check out the comments
# in solution.py from the previous lecture.
# Use to same seed to make debugging easier
np.random.seed(42)
n_records, n_features = features.shape
last_loss = None
# Initialize weights
weights = np.random.normal(scale=1 / n_features**.5, size=n_features)
# Neural Network hyperparameters
epochs = 1000
learnrate = 0.5
for e in range(epochs):
del_w = np.zeros(weights.shape)
for x, y in zip(features.values, targets):
# Loop through all records, x is the input, y is the target