2021.5.14 2022蓝桥杯练习赛2

2021.5.14 2022蓝桥杯练习赛2

闲话：
1、就难度而言，练习赛2较练习赛1有了一定的提高，可能开始会有点不太自信，但这是属于正常现象，多练就会做了。
2、就体验而言，这场练习赛有一两个题需要认真读题，题目没有想的那么简单，还是有一定思考和有一点小坑的 。
3、没什么，昨天是2021年5月13号，需要记住的日子。

题目
1、试题 算法训练 筛选号码
解析：本题真的是一道在经典不过的题目了，解题是应该要看一眼就知道这是裸的约瑟夫环问题，直接上公式就可以了。当然厉害一点的也可以去模拟这个过程，数据n<10000应该也是可以的。

公式：s=(s+m)%i; （s为值，初始为0，m表示每次从1开始的第m个人出去，记得输出答案是s+1，和for循环从i=2开始）

查漏补缺：约瑟夫环——公式法（递推公式）
推荐这篇博文，当时我也是看的这篇去理解的约瑟夫环问题

#include
using namespace std;
int main()
{
     
	int n,s=0;
	cin>>n;
	for(int i=2;i<=n;i++)
	{
     
		s=(s+3)%i;
	}
	cout<<s+1;
}

----------------------------------------------------------------------------------------------

2、试题 算法训练 最大体积

解析：本题感觉跟完全背包有点像，但在完全背包的基础上有点改动，归结为完全背包的拓展+数学思维。本题虽然数据较小，但我觉得这题还是不能纯暴力乱搞，当然主要是我也不会。
思路：
1、首先我们应该考虑什么情况会使得有无限解。经过我非非非常认真的思考， 我发现，如果所有体积的gcd值为1的时候，我们可以组成无数多种情况，这样一直组成下去，总会存在比当前认为的最大值更大的数。所以此时就有无限解输出0。（可能是我的LJ编译器不支持gcd和__gcd(a,b)函数同时使用，不然会无法识别我的gcd什么的，所以代码中用变量t记录所有体积的gcd值 ）
2、现在我们知道是有限解了，那么怎么求值可能又是大家遇到的第二个问题。
因为输出最大不可能值，没有其他限制条件，那么直接从大到小遍历vis数组找到第一个vis[i]==0就可以了，下标即答案。
3、怎么给vis数组赋值。这就是完全背包的问题了。上次发了背包九讲问题的学习链接，应该都会完全背包了，这里就不细说了。

#include
using namespace std;
typedef long long ll;
const int N=1e5+5;
ll n,t;
ll a[15];
bool vis[N];

bool check(){
     
    for(int i=1;i<=n;i++){
     
        t=__gcd(t,a[i]);
    }
    return t==1;
}

int main(){
     
    cin>>n;
    for(int i=1;i<=n;i++){
     
        cin>>a[i];
        vis[a[i]]=1;
    }
    if(check()){
     
        for(int i=1;i<=n;i++){
     
            for(int j=a[i];j<N;j++){
     
                vis[j]|=vis[j-a[i]];
            }
        }
        for(int i=N-1;;i--){
     
            if(!vis[i]){
     
                cout<<i<<"\n";
                return 0;
            }
        }
    }
    else puts("0");
}

-----------------------------------------------------------------------------------------------

3、试题 算法提高 笨小猴

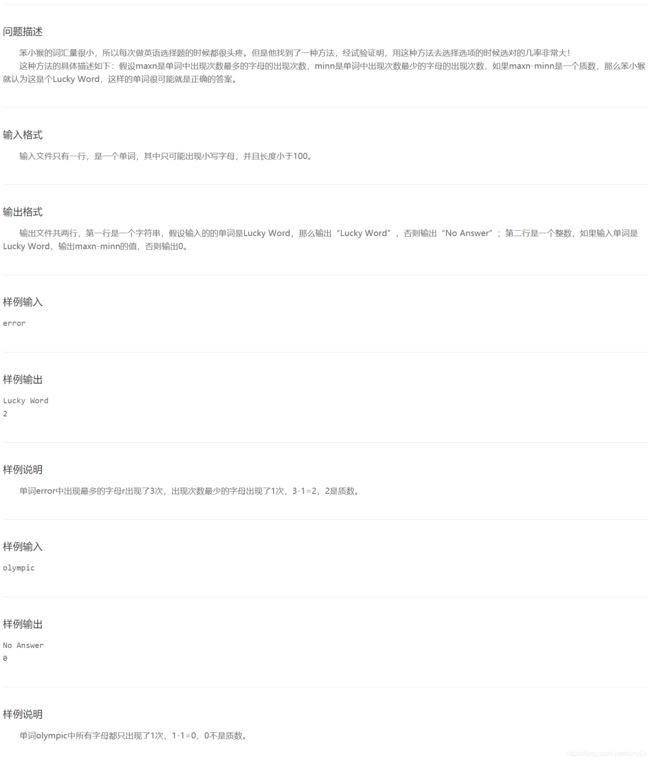
解析：这个题是我这次没有一发ac的题，但这个题是真的是个**题
可以使用map来记录’a’~~'z’中每个字符出现的次数。记得每个字符初始出现的此处都是0，且输入字符串没有某字符时，该字符对应的a[i]值也是0，这一点需要在求最小值的时候特别注意。其他的应该没什么，就是考对使用map的使用。

#include
using namespace std;
const int inf=0x3f3f3f3f;
map<int,int>a;
string s;
int maxn=-inf,minn=inf,cha;
int main(){
     
    cin>>s;
    for(int i=0;i<s.length();i++){
     
        a[s[i]-'a']++;  //使mp中字符'a'对应数字0，字符'b'对应数字1....字符'z'对应数字25，这样后面遍历顺眼点
    }
    for(int i=0;i<26;i++){
     
        maxn=max(maxn,a[i]);
        if(a[i]!=0) minn=min(minn,a[i]);  //a[i]值等于0即代表没有出现过该字符，不予考虑
    }
    cha=maxn-minn;
    if(cha==1||cha==0){
     
        cout<<"No Answer\n"<<"0";
        return 0;       
    }
    for(int i=2;i<cha;i++){
     
        if(cha%i==0){
     
            cout<<"No Answer\n"<<"0";
            return 0;
        }
    }
    cout<<"Lucky Word\n"<<cha;
}

-----------------------------------------------------------------------------------------------

4、试题 算法提高 学霸的迷宫

解析：这类走迷宫问题，百分之九十九会用到bfs算法
这都不能说是算法了，在平常的算法比赛中bfs是一种必备的基础技能，需要掌握。这题是在问 走出迷宫的最短路径长度问题的基础上，加上输出最短路径，其他的都一模一样。
十分巧的是上学期我的一个课设题目就是迷宫问题，且要求跟这个题目大同小异，十分感谢涛哥当时教了我一手，所以这个题基本就被我水过去了。（加粗感谢涛哥）
思路：
1、跟普通的走迷宫问题一样，我利用队列queue的先进先出的特性，来遍历每个到达的点，因为每个节点的信息不只是x,y，还有一个走到的step需要记录，所以这里用pair是不太现实的了，不过没有关系，我可以用struct，这是没得丝毫影响的。当到了点(n,m)时，输出当前step的就是最小步数了。我们就成功解决了第一小问。
2、第二小问是输出路径。这个要求是如果有多条长度相同的最短路径，选择在此表示方法下字典序最小的一个。这个为难了我，平时写dx数组、dy数组的写法，不过这都问题不大，就是看着感觉别扭 。剩下的就是这for循环四个方向的时候，去记录一下该次操作是什么，我这里用cz数组记录的是第几种操作，开始用to数组打表相应操作，最后输出就可以了。

#include
using namespace std;
const int N=505;
int n,m;
char mp[N][N];
bool vis[N][N];
int cz[N][N];
int dx[5]={
     1,0,0,-1};
int dy[5]={
     0,-1,1,0};
char to[5]={
     "DLRU"};
struct node{
     
    int x,y,step;
};
queue<node>q;

void bfs(){
     
    q.push({
     1,1,0});
    vis[1][1]=1;

    while(!q.empty()){
     
        node t=q.front();
        q.pop();
        if(t.x==n&&t.y==m){
     
            cout<<t.step<<"\n";
            return;
        }
        for(int i=0;i<4;i++){
     
            /*
            这里我们是从队列中读出了队首的结构体单位，当前处在点(t.x,t.y)上，在不管下一个走到的节点是否是合法状态的情况下，
            我们都有这上下左右四种走法。当然实际情况中下一步需要满足合法状态。
            合法状态：1、在这个迷宫里面，即(nx>=1&&nx<=n&&ny>=1&&ny<=m)
                     2、是否可以走，即(mp[nx][ny]=='0')。因为题目限制了mp[nx][ny]=='1'是不可以走的
                     3、是否是第一次走到该点，即(vis[nx][ny]==0)。因为如果不是第一次走到该点，是否意味着我们走了一段环形
                     的路，走完那一圈，我们又回到了该点，这样明显不符合最短路径的情况
            一般处理的方法：从起点走到终点----就是我下面这种
            另类的处理方法：从终点走到起点(????这是什么鬼)----这种基本不会用，因为有的题目并不能保证起点到终点一定有路，
                           这种无解的情况根据不同的题目会有不同的特定输出。这里不用管，因为蓝桥不会这么恶心人（QwQ）
            */
            /*
            首先，我们讲上下左右按照字典序排序好(下左右上--DLRU)，当然dx、dy数组也得相应变换。我们从起点到终点，每次都
            将通过cz数组记录好我们走到该后进行下一步的操作是什么，来为后面的Step函数做准备。
            */
            int nx=t.x+dx[i];     
            int ny=t.y+dy[i];
            int nstep=t.step+1;
            if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&mp[nx][ny]=='0'&&!vis[nx][ny]){
     
                cz[nx][ny]=i;   //注释（1）
                q.push({
     nx,ny,nstep});
                vis[nx][ny]=1;
            }
        }
    }
}

void Step(int n,int m){
         //另类的从终点到起点
    if(n==1&&m==1) return;   //此时我们是不是已经到达了起点，我们就可以结束掉Step函数
    /*
    每一次往回走，就是开始是t.x+dx[i],t.y+dy[i]；那么现在就是-dx[i],-dy[i]
    此时减去的cz[n][m]的值，是不是恰好对应了  上面注释（1）记录的第i类变化。
    就这样一直往起点走，到了起点就return，同时每一次Step后后加上输出语句，这里就刚好再次转变成从起点往终点输出了
    */
    Step(n-dx[cz[n][m]],m-dy[cz[n][m]]); 
    cout<<to[cz[n][m]];
}

int main(){
     
    cin>>n>>m;
    for(int i=1;i<=n;i++){
     
        for(int j=1;j<=m;j++){
     
            cin>>mp[i][j];
        }
    }
    bfs();
    Step(n,m);
}

-----------------------------------------------------------------------------------------------

5、试题 算法训练 友好数

解析：本题应该是本场最简单的题。没有小细节，也没有考算法，唯一考了就是C语言基础。用suma、sumb分别记录a、b除开自身的约数和。然后if(suma==b && sumb == a) 为真就输出yes，否则就输出no。 数据才10000，直接两次for循环解决。

#include
using namespace std;
int a,b;
int suma,sumb;

int main(){
     
    cin>>a>>b;
    for(int i=1;i<a;i++){
     if(a%i==0) suma+=i;}
    for(int i=1;i<b;i++){
     if(b%i==0) sumb+=i;}
    if(suma==b&&sumb==a) puts("yes");
    else puts("no");
}

-----------------------------------------------------------------------------------------------

6、试题 算法提高 高精度乘法

解析：这个题是一个好题，反正我是不太会。
Python
C++（龚神）

C++（自己）

Java（队友）

FFT学习链接
这类高精题我还是挺喜欢用Python的，根据代码长度占用空间来看，很明显的发现码量:Python(40B) （龚神的代码还加了一些其他的东西，所以会比我的代码长些，但本质都一样，没有不同。）

可惜我Python学艺不精只a90分；
Java是队友以前帮我写的，就是用Java中的大数，然后就莫名其妙的ac了；
C++是龚神以前帮我写的，当时不会NTT，（现在也不怎么会，但也有了自己的NTT板子，跟巨佬差距还是挺大的）

思路：好好学习，去看看FFT或NTT。平时大家肯定主要都是用C++做题，而且在蓝桥的竞赛中，报名了C/C++组，中途是不能用Java或Python去解题的。所以最好还是要会用C++做题。

这里我仅贴出代码，有兴趣的同学可以课余自己去了解。

Java代码- - -队友的解法

import java.io.*;
import java.math.*;
import java.util.*;
import java.text.*;

public class Main {
     
	public static void main(String[] args) {
     
		  Scanner cin = new Scanner (new BufferedInputStream(System.in));
		  BigDecimal a=cin.nextBigDecimal();
		  BigDecimal b=cin.nextBigDecimal();
		  BigDecimal ans=a.multiply(b);
		  System.out.println(ans.toString());
	}

}

-----------------------------------------------------------------------------------------------
C++代码- - -龚神的模板

#include 
using namespace std;
const int MAXN = 1e6+10, P = 998244353, G = 3, Gi = 332748118;

string s;
int cnta, cntb;
int limit = 1, L, rev[MAXN];
long long a[MAXN], b[MAXN];

int cs(long long *A) {
     
	for(int i = 0;i < s.length(); i++) A[i] = s[i]-'0';
	return (int)s.length();
}

inline long long fastpow(long long a, long long k) {
     
	long long base = 1;
	while(k) {
     
		if(k & 1) base = (base * a ) % P;
		a = (a * a) % P;
		k >>= 1;
	}
	return base % P;
}

inline void NTT(long long *A, int type) {
     
	for(int i = 0; i < limit; i++) 
		if(i < rev[i]) swap(A[i], A[rev[i]]);
	for(int mid = 1; mid < limit; mid <<= 1) {
     
		long long Wn = fastpow( type == 1 ? G : Gi, (P - 1) / (mid << 1));
		for(int j = 0; j < limit; j += (mid << 1)) {
     
			long long w = 1;
			for(int k = 0; k < mid; k++, w = (w * Wn) % P) {
     
				int x = A[j + k], y = w * A[j + k + mid] % P;
				A[j + k] = (x + y) % P,
				A[j + k + mid] = (x - y + P) % P;
			}
		}
	}
}

void init() {
     
	for(int i = 0;i < MAXN; i++) {
     
		a[i] = 0; b[i] = 0;
	}
}

int main() {
     
	while(cin >> s) {
     
		init();
		cnta = cs(a);
		cin >> s;
		cntb = cs(b);
		
		while(limit <= cnta + cntb) limit <<= 1, L++;
		for(int i = 0; i < limit; i++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (L - 1));
		
		NTT(a, 1); NTT(b, 1);
		for(int i = 0;i < limit; i++) a[i] = (a[i]*b[i]) % P;
		NTT(a, -1);
		long long inv = fastpow(limit, P-2);
		
		for(int i = 0;i <= cnta+cntb; i++) a[i] = (a[i]*inv)%P;
		vector <int> res;
		int jin = 0;
		for(int i = cnta+cntb-2; i >= 0; i--) {
     
			int now = a[i];
			now += jin;
			jin = now/10;
			now %= 10;
			res.push_back(now);
		}
		while(jin) {
     
			res.push_back(jin%10);
			jin /= 10;
		}
		
		reverse(res.begin(), res.end());
		for(int i = 0;i < res.size(); i++) printf("%d", res[i]); puts("");
	}
}

-----------------------------------------------------------------------------------------------
C++代码- - -自己的模板

#include
#include
#include
#include
#define IOS ios::sync_with_stdio(0)
using namespace std;
typedef long long ll;
const ll N=5e6+5;
const double pi=acos(-1);
string s;
ll n,m,limit,c[N];


struct complex{
     
	double real,imag;
	complex(double X=0,double Y=0){
     real=X;imag=Y;}
}a[N],b[N];

inline complex operator +(complex a,complex b){
     return complex(a.real+b.real,a.imag+b.imag);}
inline complex operator -(complex a,complex b){
     return complex(a.real-b.real,a.imag-b.imag);}
inline complex operator *(complex a,complex b){
     return complex(a.real*b.real-a.imag*b.imag,a.real*b.imag+a.imag*b.real);}

void FFT(complex *a,ll op){
     
	for(ll i=0;i<limit;i++){
     if(i<c[i]) swap(a[i],a[c[i]]);}
	for(ll mid=1;mid<limit;mid<<=1){
     
		complex W(cos(pi/mid),op*sin(pi/mid));
		for(ll r=mid<<1,j=0;j<limit;j+=r){
     
			complex w(1,0);
			for(ll l=0;l<mid;l++,w=w*W){
     
				complex x=a[j+l],y=w*a[j+mid+l];
				a[j+l]=x+y; a[j+mid+l]=x-y;
			}
		}
	}
}

int main(){
     
	 IOS; 
	 cin>>s; n=s.size()-1;
	 for(ll i=0;i<=n;i++) a[n-i].real=s[i]-48;
	 cin>>s; m=s.size()-1;
	 for(ll i=0;i<=m;i++) b[m-i].real=s[i]-48;
	 limit=1;
	 
	 ll l=0;
	 while(limit<=n+m){
     
	 	limit<<=1;
	 	l++;
	 }
	 
	 for(ll i=0;i<limit;i++) c[i]=(c[i>>1]>>1)|((i&1)<<(l-1));
	 FFT(a,1);FFT(b,1);
	 for(ll i=0;i<=limit;i++) a[i]=a[i]*b[i];
	 FFT(a,-1);
	 
	 memset(c,0,sizeof(c));
	 for(ll i=0;i<=n+m+1;i++) c[i]=a[i].real/limit+0.5;
	 for(ll i=0;i<=n+m;i++){
     
	 	c[i+1]+=c[i]/10;
	 	c[i]%=10;
	 }
	 limit=n+m+1;
	 while(c[limit]){
     
	 	c[limit+1]+=c[limit]/10;
	 	c[limit]%=10;
	 	limit++;
	 }
	 
	 for(ll i=limit-1;i>=0;i--) cout<<c[i];
	 return 0;
}

-----------------------------------------------------------------------------------------------

总结

1、本次可能有那么几道有难度的题，千万别灰心，多问，多做题，多学算法。一段时间后编程水平会有显著提高的。只要认真学了，这是必然的。
2、还是要背一些通用模板的 ，大部分平时用的多模板是要知道的，多用可以加深印象，但最好是在理解的基础上多去码几遍模板。正式的蓝桥杯是不能带模板进去的，所以认为有用的模板最好记到脑子里。虽然我也不记得这里的fft模板。
3、学习虽然重要，但还是得加强身体锻炼。比赛长达4小时，有的长达5小时，这还真不是一件容易的事。加强锻炼，在比赛等其他方面才更有优势。