unity 贝塞尔曲线算法
在任意几个点坐标绘制出的一条曲线,就叫贝赛尔曲线。
线性公式
![]() 等同于线性插值
等同于线性插值
这个最简单,就是很普通的插值算法,给定p0,p1,t取值范围0到1
// 线性
Vector3 Bezier(Vector3 p0, Vector3 p1, float t)
{
return (1 - t) * p0 + t * p1;
}二次方公式
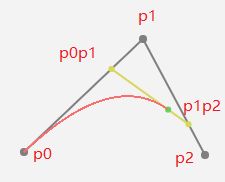
![]()
p0p1 = (1 - t) * p0 + t * p1;
p1p2 = (1 - t) * p1 + t * p2;
B(t) = (1 - t) * p0p1 + t * p1p2;
B(t) = ((1 - t) * ((1 - t) * p0 + t * p1)) + (t * ((1 - t) * p1 + t * p2))
二次方的也不是很难理解,还是求插值,p0和p1的插值,p1和p2的插值,在求这两个插值(vector3)的插值
// 二阶曲线
Vector3 Bezier(Vector3 p0, Vector3 p1, Vector3 p2, float t)
{
Vector3 p0p1 = (1 - t) * p0 + t * p1;
Vector3 p1p2 = (1 - t) * p1 + t * p2;
Vector3 result = (1 - t) * p0p1 + t * p1p2;
return result;
}三次方公式
![]()
p0p1 = (1 - t) * p0 + t * p1;
p1p2 = (1 - t) * p1 + t * p2;
p2p3 = (1 - t) * p2 + t * p3;
p0p1p2 = (1 - t) * p0p1 + t * p1p2;
p1p2p3 = (1 - t) * p1p2 + t * p2p3;
B(t) = (1 - t) * p0p1p2 + t * p1p2p3;
三次方的曲线其实和二次没有太大区别,不过是多了一个点,就多了一层要计算的插值
// 三阶曲线
Vector3 Bezier(Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3, float t)
{
Vector3 result;
Vector3 p0p1 = (1 - t) * p0 + t * p1;
Vector3 p1p2 = (1 - t) * p1 + t * p2;
Vector3 p2p3 = (1 - t) * p2 + t * p3;
Vector3 p0p1p2 = (1 - t) * p0p1 + t * p1p2;
Vector3 p1p2p3 = (1 - t) * p1p2 + t * p2p3;
result = (1 - t) * p0p1p2 + t * p1p2p3;
return result;
}n次方公式
最后一个,最难的n次方的公式,其实这个只要能把前面两个理解了,最后一个也不难,都是有规律的,就是不停的去计算插值;点1和点2插值,产生出新的点,点2和点3插值,又产生一个点,依次循环,直到最后只剩下一个点。
// n阶曲线,递归实现
public Vector3 Bezier(float t, List p)
{
if (p.Count < 2)
return p[0];
List newp = new List();
for (int i = 0; i < p.Count - 1; i++)
{
Debug.DrawLine(p[i], p[i + 1]);
Vector3 p0p1 = (1 - t) * p[i] + t * p[i + 1];
newp.Add(p0p1);
}
return Bezier(t, newp);
}
// transform转换为vector3,在调用参数为List的Bezier函数
public Vector3 Bezier(float t, List p)
{
if (p.Count < 2)
return p[0].position;
List newp = new List();
for (int i = 0; i < p.Count; i++)
{
newp.Add(p[i].position);
}
return Bezier(t, newp);
} 
在unity里实现的效果