人工智能-算法模型-线性回归

阅读此篇前, 建议先对梯度下降法有所了解人工智能-数学基础-函数与优化

一.概述

       回归分析是研究统计规律的方法之一。在回归分析中我们把所关心的一些指标称为因变量，通常用Y来表示；影响因变量的变量称为自变量，用X1、X2、…XP来表示。回归分析研究的主要问题是：确定Y与X1、X2、…XP间的定量关系表达式，这种表达式称为回归方程；对求得的回归方程的可信度进行检验，判断自变量对Y有无影响；利用所求得的回归方程进行预测和控制。

       线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为 y = w’x+e，e为误差服从均值为0的正态分布。
       回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析（平面中的直线）。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析（超立方体中的直线）。

$$\hat{y}(w,x)=w_0+w_1{x}_1+\cdots +w_p{x}_p$$

二.线性回归实现

我们先了解几个概念:
$$形如y=x\cdot w+b的模型均为线性模型$$
$$形如L=\mathbb{E}[\frac{1}{2}(y-d{)}^2]称为均方误差(MSE)$$
$$使用MSE作为损失函数的模型称为最小二乘法。$$
$$最小二乘法告诉我们目标是什么,然后大部分情况下可以使用梯度下降法来实现。$$
$$如果预测的值是连续的,则该机器学习模型称为：回归模型。$$
$$线性模型+回归模型=线性回归$$

2.1 利用梯度下降法实现线性回归

梯度下降法的原理在我的另一篇博客: 机器学习-数学基础-函数与优化

"""
基于梯度下降法的线性回归
"""
import numpy as np
import matplotlib.pyplot as plt

plt.switch_backend("TkAgg")


# 一. 模拟训练集数据

# 制造特征, 以x=0为对称轴, 标准差为1的正态分布生成1000个点
x = np.random.normal(0, 1, [1000])
# 制造标签, 以一个一元一次方程加上噪声
d = 2 * x + 5 + np.random.normal(0, 0.5, [1000])


# 二.构建机器学习模型

# 构建一元一次方程的机器学习模型 y = ax + b
def model(x, a, b):
    return a * x + b


# 损失函数为: L = 0.5 (y - d)^2, 此为我们的目标函数
#  对目标函数分别求 a, b 的偏导(梯度)
def grad(x, d, a, b):
    # 对 L 求 a, b 的偏导
    y = model(x, a, b)
    dLdy = (y - d)
    dLda = np.mean(dLdy * x)
    dLdb = np.mean(dLdy * 1)
    # 损失值
    L = np.mean(0.5 * (y - d) ** 2)
    return dLda, dLdb, L


# 三. 进行函数的优化

# 为可训练参数定义初始值
a = 0
b = 0
# 定义超参数学习率
eta = 0.3

# 开始进行迭代
for step in range(200):
    ga, gb, L = grad(x, d, a, b)
    a = a - eta * ga
    b = b - eta * gb
    print("a : %s, b: %s" % (a, b))

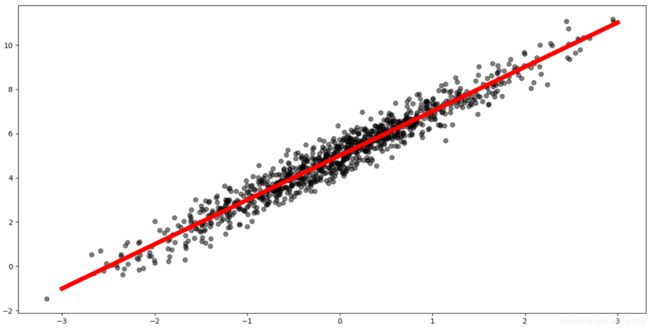
print("迭代结束后的 a : %s, b: %s" % (a, b))

# 绘制原始数据图,颜色为黑色, 透明度为0.5
plt.scatter(x, d, color="k", alpha=0.5)

# 绘制拟合后的直线, 颜色为红色, 宽度为6
x_plt = np.linspace(-3, 3, 100)
y_plt = model(x_plt, a, b)
plt.plot(x_plt, y_plt, color="r", lw=6)

plt.show()

迭代结束后的 a : 2.013884999773956, b: 5.003882110267274

可以看到, 跟我们预设的训练集的函数很接近

2.2 sk-learn 实现线性回归

"""
线性回归(一元线性回归)

LinearRegression基于最小二乘法
"""
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import numpy as np

plt.switch_backend("TkAgg")

# 一. 模拟训练集数据

# 制造特征, 以x=0为对称轴, 标准差为1的正态分布生成1000个点
x = np.random.normal(0, 1, [1000])
# 制造标签, 以一个一元一次方程加上噪声
d = 2 * x + 5 + np.random.normal(0, 0.5, [1000])
# 将x和d转为sk-learn认识的格式
x = np.array(x).reshape(1000, 1)
d = np.array(d).reshape(1000, 1)

# 绘制原始数据图,颜色为黑色, 透明度为0.5
plt.scatter(x, d, color="k", alpha=0.5)

# 二. 模型训练
# 基于x, d建立模型
model = LinearRegression()
model.fit(x, d)

# 绘制拟合后的直线, 颜色为红色, 宽度为6
x_plt = np.linspace(-3, 3, 100)
x_plt = np.array(x_plt).reshape(100, 1)
y_plt = model.predict(x_plt)
# 将多维数组转为一维
x_plt = x_plt.flatten()
y_plt = np.array(y_plt).flatten()
plt.plot(x_plt, y_plt, color="r", lw=6)

plt.show()

# 打印系数和截距, 分别对应上一个程序的 a 和 b
print("迭代结束后的 系数 : %s, 截距: %s" % (model.coef_, model.intercept_))

迭代结束后的 系数 : [[1.97161116]], 截距: [4.96504692]

三.多项式回归

多项式回归为一种广义上的线性回归(即线性回归中x的系数不全为1):
$$如:\hat{y}(w,x)=w_0+w_1{x}_1+w_1{x}_2+w_3{x}_1^2+w_4{x}_2^2+\cdots +w_p{x}_p^n$$

3.1 梯度下降法进行多项式回归

"""
多项式回归( 梯度下降法)
"""
import numpy as np
import matplotlib.pyplot as plt

plt.switch_backend("TkAgg")

# 一. 模拟训练集数据

# 制造特征, 以x=0为对称轴, 标准差为1的正态分布生成1000个点
x = np.random.normal(0, 1, [1000])
# 制造标签, 以一个一元三次方程加上噪声
d = x ** 3 + 3 * x ** 2 + 2 * x + 5 + np.random.normal(0, 2, [1000])


# 二.构建机器学习模型
# 构建一元三次方程的机器学习模型 y = ax^3 + bx^2 + cx +k
def model(x, a, b, c, k):
    return a * x ** 3 + b * x ** 2 + c * x + k


# 损失函数为: L = 0.5 (y - d)^2, 此为我们的目标函数
#  对目标函数分别求 a, b, c, k 的偏导(梯度)
def grad(x, d, a, b, c, k):
    y = model(x, a, b, c, k)
    dLdy = (y - d)
    dLda = np.mean(dLdy * x ** 3)
    dLdb = np.mean(dLdy * x ** 2)
    dLdc = np.mean(dLdy * x)
    dLdk = np.mean(dLdy * 1)
    # 损失值
    L = np.mean(1 / 2 * (y - d) ** 2)
    return dLda, dLdb, dLdc, dLdk, L


# 三. 进行函数的优化

# 为可训练参数定义初始值
a = 1
b = 1
c = 1
k = 1
# 定义超参数学习率
eta = 0.1

# 开始进行迭代
for step in range(1000):
    ga, gb, gc, gk, L = grad(x, d, a, b, c, k)
    a = a - eta * ga
    b = b - eta * gb
    c = c - eta * gc
    k = k - eta * gk
    print("a : %s, b: %s, c : %s, k: %s" % (a, b, c, k))

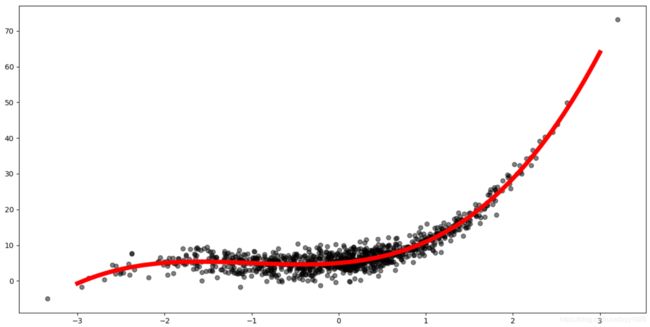
print("迭代结束后的 a : %s, b: %s, c : %s, k: %s" % (a, b, c, k))

# 绘制原始数据图,颜色为黑色, 透明度为0.5
plt.scatter(x, d, color="k", alpha=0.5)

# 绘制拟合后的曲线, 颜色为红色, 宽度为6
x_plt = np.linspace(-3, 3, 100)
y_plt = model(x_plt, a, b, c, k)
plt.plot(x_plt, y_plt, color="r", lw=6)

plt.show()

迭代结束后的 a : 1.0254913173071005, b: 2.8978685090191756, c : 1.9014938313936285, k: 5.092306822156842

3.2 sklearn进行多项式回归

"""
多项式回归( sk-learn)
"""
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.pipeline import Pipeline
import numpy as np
import matplotlib.pyplot as plt

plt.switch_backend("TkAgg")


# 一. 模拟训练集数据

# 制造特征, 以x=0为对称轴, 标准差为1的正态分布生成1000个点
x = np.random.normal(0, 1, [1000])
# 制造标签, 以一个一元三次方程加上噪声
d = x ** 3 + 3 * x ** 2 + 2 * x + 5 + np.random.normal(0, 2, [1000])
# 将x和d转为sk-learn认识的格式
x = np.array(x).reshape(1000, 1)
d = np.array(d).reshape(1000, 1)

# 绘制原始数据图,颜色为黑色, 透明度为0.5
plt.scatter(x, d, color="k", alpha=0.5)

# 二. 模型训练
model_process = [('poly', PolynomialFeatures(degree=3)),  # 多项式次幂,degree为幂数
                 ('standard', StandardScaler()),  # 归一化数据
                 ('linear_reg', LinearRegression())]  # 线性回归

model = Pipeline(model_process)
model.fit(x, d)


# 绘制拟合后的曲线, 颜色为红色, 宽度为6
x_plt = np.linspace(-3, 3, 100)
x_plt = np.array(x_plt).reshape(100, 1)
y_plt = model.predict(x_plt)
# 将多维数组转为一维
x_plt = x_plt.flatten()
y_plt = np.array(y_plt).flatten()
plt.plot(x_plt, y_plt, color="r", lw=6)

plt.show()

四. 利用批尺寸训练数据

以上程序我们采用的是每次迭代都代入全量数据, 我们还可以怎么做呢?

1. 如果数据集比较小，可采用全数据集进行训练(Full Batch Learning), 由全部训练数据确定的方向能够更好地代表样本总体，从而更准确地指向极值的方向。


2. 但是对于过大数据集, 由于机器性能的原因, 无法一次性加载计算过大数据,所以我们需要进行批尺寸划分数据(Batch Size)。

4.1 批尺寸的取值

1.如果Batch Size 过小, 跑完一次全数据集(epoch)需要的迭代次数更多, 导致训练速度过慢, 并且相邻 mini-batch 间的差异相对较大, 会导致相邻两次迭代的震荡情况比较严重, 不利于收敛。如此 Batch Size为1, 则我们称之为随机梯度下降, 这会失去矩阵运算带来的速度优势, 但因为样本点不同, 每次迭代梯度都是随机下降或震动, 这有可能在面对某些目标函数的时候, 会跳出局部最小值的陷阱。


2.在一定范围内, Batch Size越大, 内存利用率越高, 大矩阵乘法的并行化效率提高, 跑完一次全数据集(epoch)所需的迭代次数越少, 对相同数据量的处理训练速度加快, 并且较大的 Batch Size 确定的下降方向更准确, 引起的梯度震荡越小。


3.如果 Batch Size 极端大, 相邻 mini-bacth 间的差异过小, 导致不同 batch 的梯度方向没有变化, 容易陷入局部极小值.并且由于在同样的 epochs下参数更新变少, 反而需要更长的迭代次数, 从而导致性能下降。

4.2 利用批尺寸拟合一元三次方程

"""
多项式回归( 梯度下降法)
采用 Mini-Batch 训练
"""
import numpy as np
import matplotlib.pyplot as plt

plt.switch_backend("TkAgg")

# 一. 模拟训练集数据

# 制造特征, 以x=0为对称轴, 标准差为1的正态分布生成1000个点
x = np.random.normal(0, 1, [1000])
# 制造标签, 以一个一元三次方程加上噪声
d = x ** 3 + 3 * x ** 2 + 2 * x + 5 + np.random.normal(0, 2, [1000])


# 二.构建机器学习模型
# 构建一元三次方程的机器学习模型 y = ax^3 + bx^2 + cx +k
def model(x, a, b, c, k):
    return a * x ** 3 + b * x ** 2 + c * x + k


# 损失函数为: L = 0.5 (y - d)^2, 此为我们的目标函数
#  对目标函数分别求 a, b, c, k 的偏导(梯度)
def grad(x, d, a, b, c, k):
    y = model(x, a, b, c, k)
    dLdy = (y - d)
    dLda = np.mean(dLdy * x ** 3)
    dLdb = np.mean(dLdy * x ** 2)
    dLdc = np.mean(dLdy * x)
    dLdk = np.mean(dLdy * 1)
    # 损失值
    L = np.mean(1 / 2 * (y - d) ** 2)
    return dLda, dLdb, dLdc, dLdk, L


# 三. 进行函数的优化

# 为可训练参数定义初始值
a = 1
b = 1
c = 1
k = 1
# 定义超参数学习率
eta = 0.1

# 对于数据量较多的情况下，我们可以采用 Batch Size进行训练。
batch_size = 100

# 开始进行迭代
for step in range(1000):

    # 此时 step 可以取值为 0-9, 可以训练所有数据, 也可采用其他分组样式
    step = step % (1000 // batch_size)
    xin = x[step * batch_size:step * batch_size + batch_size]
    din = d[step * batch_size:step * batch_size + batch_size]

    ga, gb, gc, gk, L = grad(xin, din, a, b, c, k)

    a = a - eta * ga
    b = b - eta * gb
    c = c - eta * gc
    k = k - eta * gk
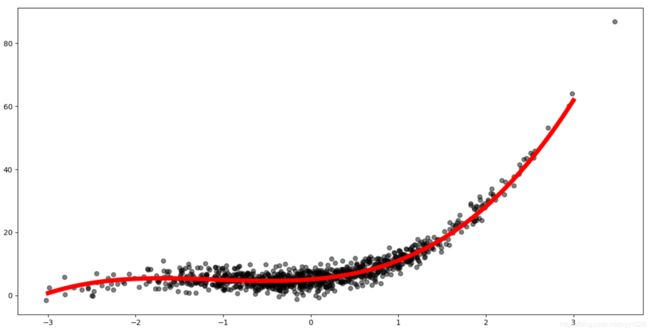
    print("a : %s, b: %s, c : %s, k: %s" % (a, b, c, k))

print("迭代结束后的 a : %s, b: %s, c : %s, k: %s" % (a, b, c, k))

# 绘制原始数据图,颜色为黑色, 透明度为0.5
plt.scatter(x, d, color="k", alpha=0.5)

# 绘制拟合后的直线, 颜色为红色, 宽度为6
x_plt = np.linspace(-3, 3, 100)
y_plt = model(x_plt, a, b, c, k)
plt.plot(x_plt, y_plt, color="r", lw=6)

plt.show()

迭代结束后的 a : 0.8918837808367376, b: 2.9145724686906496, c : 2.1669257849632313, k: 5.084371880487646

五. 数据的归一化

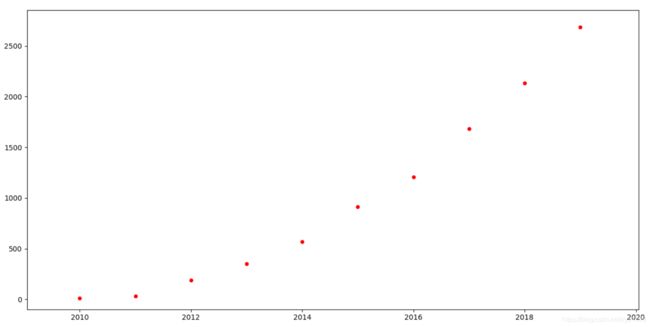
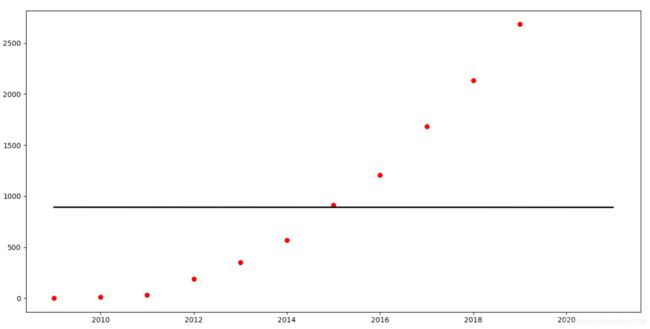
我们用某宝双十一的营业额做下预测, 我们从互联网上获取到 2011-2019年的营业额, 来预测2020年的营业额

2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019
0.5, 9.36, 33.6, 191, 350, 571, 912, 1207, 1682, 2135, 2684

绘制一下:

import numpy as np
import matplotlib.pyplot as plt

plt.switch_backend("TkAgg")

x = [2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019]
x = np.array(x)
d = [0.5, 9.36, 33.6, 191, 350, 571, 912, 1207, 1682, 2135, 2684]
d = np.array(d)

plt.scatter(x, d, marker="o", c="r", s=20)
plt.show()

我们通过观察, 预测模型为一元二次函数:

5.1 我们先用原始数据进行预测

"""
6. 预测 2020 年 双十一销售额
"""
import numpy as np
import matplotlib.pyplot as plt

plt.switch_backend("TkAgg")

# 一. 准备训练集数据

x = [2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019]
x = np.array(x)
d = [0.5, 9.36, 33.6, 191, 350, 571, 912, 1207, 1682, 2135, 2684]
d = np.array(d)


# 二.构建机器学习模型

# 建立数学模型, ax^2 + bx + c, abc为可训练参数
def model(x, a, b, c):
    return a * x ** 2 + b * x + c


# 损失函数为: L = 0.5 (y - d)^2, 此为我们的目标函数
#  对目标函数分别求 a, b 的偏导(梯度)
def grad(x, d, a, b, c):
    y = model(x, a, b, c)
    dLdy = (y - d)
    dLda = np.mean(dLdy * x ** 2)
    dLdb = np.mean(dLdy * x ** 1)
    dLdc = np.mean(dLdy * 1)
    return dLda, dLdb, dLdc

# 三. 进行函数的优化


# 为可训练参数定义初始值
a = 1
b = 1
c = 0
# 定义超参数学习率
eta = 0.0000000000001

# 开始进行迭代
for step in range(1000):
    ga, gb, gc = grad(x, d, a, b, c)
    a -= eta * ga
    b -= eta * gb
    c -= eta * gc
    print("a : %s, b: %s, c: %s" % (a, b, c))

predict = model(2020, a, b, c)
print("2020年销售额预测: %s" % predict)

# 绘制拟合后的直线, 颜色为灰色, 宽度为2
x_plt = np.linspace(2009, 2021, 100)
y_plt = model(x_plt, a, b, c)
plt.plot(x_plt, y_plt, color="k", lw=2)

# 绘制原始数据图,颜色为红色
plt.scatter(x, d, color="r")
plt.show()

可以看到, 在这里, 学习率定为 0.0000000000001 ,得出的曲线明显欠拟合, 而把学习率稍微调大些, 则直接训练出错报错，这是由于 以年份直接做特征，可能会导致每次迭代得到的梯度过大，而导致不收敛。如我把学习率定位如下 0.1，打印 ga，gb，gc 三个梯度：

ga : -2.113527971083052e+245, gb: -1.0494102976389005e+242, gc: -5.210551754324035e+238
ga : 3.4773819527572355e+257, gb: 1.7265919732196034e+254, gc: 8.572906950982553e+250
ga : -5.7213272834829e+269, gb: -2.8407571840048394e+266, gc: -1.4104981018414135e+263
ga : 9.413284571391757e+281, gb: 4.673890243696101e+278, gc: 2.3206887776499316e+275
ga : -1.548765208342707e+294, gb: -7.689939194071007e+290, gc: -3.818223077138074e+287
ga : 2.5481792804423668e+306, gb: 1.2652236515024691e+303, gc: 6.282112279421257e+299
ga : -inf, gb: -inf, gc: -inf
ga : inf, gb: inf, gc: inf
ga : nan, gb: nan, gc: nan
ga : nan, gb: nan, gc: nan

各个梯度已经大到超越计算机数字的范围了

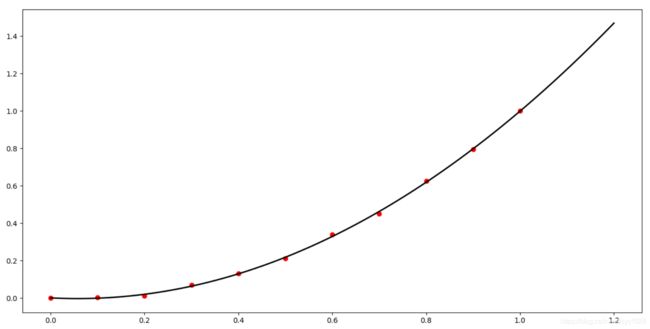
5.2 数据的归一化

1.归一化是一种简化计算的方式，即将有量纲的表达式，变换为无量纲的表达式，成为标量。目的是让大的输入，大的信号映射到小范围里面。


2.据归一化后，最优解的寻优过程会变得平缓，更容易收敛，提升模型的收敛速度。


3.归一化可以提高模型训练精度，在一些涉及距离计算的算法时效果显著，比如算法中要计算欧氏距离，取值范围较大的特征比取值范围较小的特征对结果的影响会更大，所以会导致精度损失，而归一化可以使各个特征向量对结果的影响趋于相同。

归一化/标准化常用方式:

1.对原始数据进行放缩, 将数据归一到[0,1]中间, 这种方法的缺陷是当有新数据加入时, 可能导致max和min的变化, 所以这种方法只适用于数据在一个范围内分布的情况。在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用归一化方法。

$$\hat{X}=\frac{x-x_{min}}{|x_{max}-x_{min}|}$$

其他一些标准化/归一化方式(注:标准化和归一化是有区别的, 本章不重点叙述):

2. 将数据放缩到 [-1, 1]区间

$$\hat{X}=\frac{x-\bar{x}}{|x_{max}-x_{min}|}$$

3.如果数据的分布本身就服从正态分布, 可以使数据减去均值然后除以方差(或标准差), 这种数据标准化方法经过处理后数据符合标准正态分布，即均值为0，标准差为1。为防止除数为0, 可在分母上加上一个很小的数.

$$\hat{X}=\frac{x-\bar{x}}{\sigma +ϵ}$$

"""
预测 2020 年 双十一销售额( 归一化)
"""
import numpy as np
import matplotlib.pyplot as plt

plt.switch_backend("TkAgg")

# 一. 准备训练集数据

x = [2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019]
x = np.array(x)
d = [0.5, 9.36, 33.6, 191, 350, 571, 912, 1207, 1682, 2135, 2684]
d = np.array(d)


# 二.构建机器学习模型

# 建立数学模型, ax^2 + bx + c, abc为可训练参数
def model(x, a, b, c):
    return a * x ** 2 + b * x + c


# 损失函数为: L = 0.5 (y - d)^2, 此为我们的目标函数
#  对目标函数分别求 a, b 的偏导(梯度)
def grad(x, d, a, b, c):
    y = model(x, a, b, c)
    dLdy = (y - d)
    dLda = np.mean(dLdy * x ** 2)
    dLdb = np.mean(dLdy * x ** 1)
    dLdc = np.mean(dLdy * 1)
    loss = np.mean(0.5 * (y - d) ** 2)
    return dLda, dLdb, dLdc, loss


# 三. 进行函数的优化

# 为可训练参数定义初始值
a = 1
b = 1
c = 0
# 定义超参数学习率
eta = 0.2


# 进行数据的归一化, 将 x, d 的值归一到 0-1的范围
x_min = np.min(x)
x_max = np.max(x)
xn = (x - x_min) / (x_max - x_min)
d_min = np.min(d)
d_max = np.max(d)
dn = (d - d_min) / (d_max - d_min)


# 开始进行迭代
for step in range(20000):
    ga, gb, gc, loss = grad(xn, dn, a, b, c)
    a -= eta * ga
    b -= eta * gb
    c -= eta * gc
    # print("a : %s, b: %s, c: %s, 损失函数: %s" % (a, b, c, loss))

# 做预测的时候, 需要将 年份 进行归一化
predict = model((2020 - x_min) / (x_max - x_min), a, b, c)
# 取出预测值得时候需要按照归一化的规则, 反向获取真正的数值
print("2020年销售额: ", predict * (d_max - d_min) + d_min)


# 绘制拟合后的曲线, 颜色为灰色, 宽度为2(该直线为归一化之后的曲线)
x_plt = np.linspace(2009, 2021, 100)
x_plt = (x_plt - x_min) / (x_max - x_min)
y_plt = model(x_plt, a, b, c)

plt.plot(x_plt, y_plt, color="k", lw=2)

# 绘制训练数据归一化后的散点图,颜色为红色
plt.scatter(xn, dn, color="r")
plt.show()

2020年销售额:  3282.2758912241256

在我们对原始数据进行归一化后, 较好的拟合出了曲线

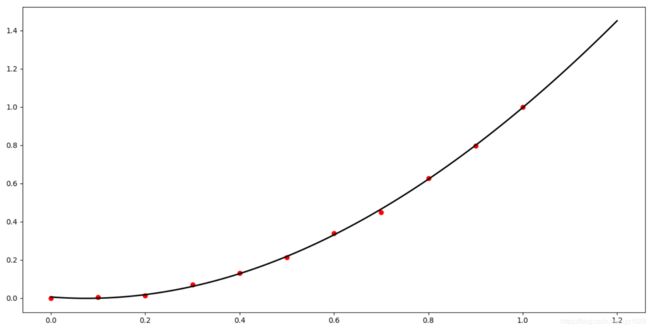
六. 利用矩阵优化程序编写

利用矩阵的乘法,优化各个梯度的计算方式, 防止每加一个系数就要多求一次偏导:

"""
预测 2020 年 双十一销售额(矩阵乘法, 一元三次方程)
"""
import numpy as np
import matplotlib.pyplot as plt

plt.switch_backend("TkAgg")

# 一. 准备训练集数据
x = [2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019]
x = np.array(x)
d = [0.5, 9.36, 33.6, 191, 350, 571, 912, 1207, 1682, 2135, 2684]
d = np.array(d)


# 二.构建机器学习模型

# 建立通用线性回归模型, y = x @ w +b, w为可训练参数向量
def model(x, w, b):
    return x @ w + b


# 损失函数为: L = 0.5 (y - d)^2, 此为我们的目标函数
#  对目标函数分别求 w, b 的偏导(梯度)
def grad(x, d, w, b):
    y = model(x, w, b)
    dLdy = (y - d)

    # 利用矩阵的乘法, x为我们为多项式构建的特征向量,
    # x.T为相同特征列表, 最终获得dLdw为 梯度的向量
    dLdw = x.T @ dLdy / len(d)
    # 为偏置参数d求偏导
    # 这里的数据集已经是二维矩阵了, 所以对列求平均
    dLdb = np.mean(dLdy, axis=0)
    loss = 0.5 * (y - d) ** 2
    return dLdw, dLdb, loss


# 为 w 向量赋予初始值, 以x=0为对称轴, 标准差为1的正态分布生成三行一列的二维矩阵
w = np.random.normal(0, 1, [3, 1])
# 为 b 赋予初始值, 注意也要协程矩阵的形式, 哪怕只有一个数
b = np.array([0.0])

# 定义超参数学习率
eta = 0.2

# 进行数据的归一化, 将 x, d 的值归一到 0-1的范围
x_min = np.min(x)
x_max = np.max(x)
xn = (x - x_min) / (x_max - x_min)
d_min = np.min(d)
d_max = np.max(d)
dn = (d - d_min) / (d_max - d_min)

# 将 xn, dn 重组为11行一列的数据, 以满足矩阵运算的要求
xn = np.reshape(xn, [11, 1])
dn = np.reshape(dn, [11, 1])

# 将 x, x^2, x^3 作为特征进行拼接
xn2 = np.concatenate([xn, xn ** 2, xn ** 3], axis=1)

# 开始迭代
for step in range(20000):
    gw, gb, loss = grad(xn2, dn, w, b)
    w -= eta * gw
    b -= eta * gb
    # print("w: %s, b: %s, 损失函数: %s: " % (w, b, loss))

print("w: %s, b: %s, 损失函数: %s: " % (w, b, loss))

# 三.模型的预测和绘制

# 做预测的时候, 需要将 年份 进行归一化
predict_x = (2020 - x_min) / (x_max - x_min)
predict_x_feature = [predict_x, predict_x ** 2, predict_x ** 3]
predict_y = model(predict_x_feature, w, b)
print(predict_y)

# 取出预测值得时候需要按照归一化的规则, 反向获取真正的数值
print("2020年销售额: ", predict_y[0] * (d_max - d_min) + d_min)


# 绘制拟合后的曲线, 颜色为灰色, 宽度为2(该直线为归一化之后的曲线)
x_plt = np.linspace(2009, 2021, 100)
x_plt = (x_plt - x_min) / (x_max - x_min)

# 将 x_plt 转为 100行1列的数据
x_plt2 = np.reshape(x_plt, [100, 1])
# 将 x_plt, x_plt^2, x_plt^3 进行拼接, 得到 100行3列的数据
x_plt2 = np.concatenate([x_plt2, x_plt2 ** 2, x_plt2 ** 3], axis=1)
# 代入到模型中
y_plt = model(x_plt2, w, b)

plt.plot(x_plt, y_plt, color="k", lw=2)

# 绘制训练数据归一化后的散点图,颜色为红色
plt.scatter(xn, dn, color="r")

plt.show()

2020年销售额:  3173.4911287547034