ElGamal密码及其安全性证明

ElGamal 在 DDH下的 IND-CPA 安全性

有关DDH和ElGamal

Diffie-Hellman Protocol

有限循环群 $\mathbb{G}$ $\left(e.gG={\left(Z_p\right)}^{\ast }\right)$，其阶数为$n$

在$G$中取生成元$g$: $<g>=\left\{1,\mathrm{g},{\mathrm{g}}^2,{\mathrm{g}}^3,\dots ,{\mathrm{g}}^{\mathrm{n}-1}\right\}$,那么Diffie-Hellman Protocol如下图所示：

通过图述方式，Alice和Bob可以共享密钥$k_{AB}$。

ElGamal体制

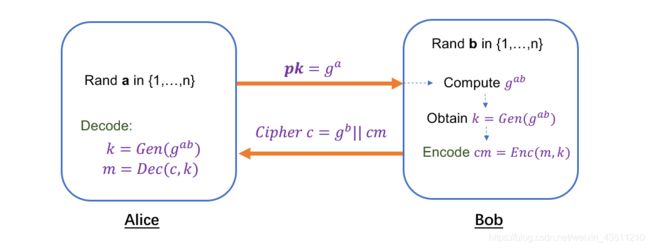
ElGamal是基于Diffie-Hellman Protocal的公钥加密方案。其同样基于有限循环群$\mathbb{G}$和群中一固定的生成元$g$，那么ElGamal可由下图描述：

（个人认为这个图比我在很多地方看到的文字叙述更容易理解。）

其中Enc，Dec是认证加密系统的加密和解密算法（比如对称加密方法），Gen是密钥生成算法。在实际应用时，Gen一般为一个Hashing Function(哈希函数)，即$$k\leftarrow Hash(g^b,g^{ab})$$

Compute Diffie-Hellman Assumption

在上图，pk为我们选择的公钥，而其实你会发现$g^a$.$g^b$都是明文形式给出的。基于$g,g^a，g^b$，得到$g^{ab}$是计算困难的, 这就是Compute Diffie-Hellman Assumption(CDH)。

Decision Diffie-Hellman Assumption

考虑阶数为$q$的有限循环群$\mathbb{G}$和群中一固定的生成元$g$，已知$g^a$,$g^b$（$a,b\in {\mathbb{Z}}_q$, 独立随机选取），若DDH Assumption成立，那么$g^{ab}$应与$\mathbb{G}$中的随机元素不可区分。

如果DDH在群$\mathbb{G}$中是困难的，那么对于所有概率多项式时间算法$\mathcal{A}$都应存在可忽略的函数$negl$，其满足：
$$\left|\mathrm{Pr}\left[\mathcal{A}\left(\mathbb{G},q,g,g^a,g^b,g^c\right)=1\right]-\mathrm{Pr}\left[\mathcal{A}\left(\mathbb{G},q,g,g^a,g^b,g^{ab}\right)=1\right]\right|\le \mathrm{negl}(n)$$
其中$a,b,c$是在${\mathbb{Z}}_q$中随机选取的。可以看出，DDH是强于CDH的假设。

ElGamal在DDH下的CPA安全性证明

由于ElGamal是一种公共密钥加密方案，因此，如果它对单个查询是安全的，则它对$q$个查询也是安全的。因此，我们可以假设对手A恰好进行了一次查询。

我们假设攻击者攻击ElGamal时具有优势$Adv\mathcal{A}$。

构建攻击实验D如下：

Require：$\mathbb{G},q,g,g^a,g^b,g^z$，Challenger， Adversary $\mathcal{A}$，El Gamal scheme $\Pi$

1. 挑战者生成公钥$pk=⟨\mathbb{G},q,g,g^a⟩$，发送给攻击者$\mathcal{A}$
2. 攻击者选择希望被加密的明文$m_0,m_1\in \mathbb{G}$
3. 挑战者随机生成$b$，向攻击者$\mathcal{A}$发送$g^b$以及挑战密文$Enc(m_b,g^z)(b=0或b=1)$
4. 攻击者$\mathcal{A}$判断密文是由哪条明文加密的，如果攻击者认为$b^{\prime }=b$则输出$b^{\prime }=1$，反之输出0。

当$z=rand$时，由于其是均匀随机选择的，所以$\mathcal{A}$以1/2的概率输出1，即：
$$\mathrm{Pr}\left[D\left(\mathbb{G},q,g,g^a,g^b,g^z\right)=1\right]=\mathrm{Pr}\left[\mathrm{Pub}{K}_{\mathcal{A},\Pi }^{\mathrm{eav}}(n)=1\right]=\frac{1}{2}$$
当$z=ab$时，此时为IND-CPA实验。

由于$x,y$是随机选择的，那么攻击者在实验中具有优势$Adv\mathcal{A}$（假设）：
$$\mathrm{Pr}\left[D\left(\mathbb{G},q,g,g^a,g^b,g^{ab}\right)=1\right]=\mathrm{Pr}\left[\mathrm{Pub}{K}_{\mathcal{A},\Pi }^{\mathrm{eav}}(n)=1\right]=\frac{1}{2}+Adv\mathcal{A}$$
由于DDH在群$\mathbb{G}$中是困难的，因此有：
$$\left|\mathrm{Pr}\left[\mathcal{A}\left(\mathbb{G},q,g,g^a,g^b,g^z\right)=1\right]-\mathrm{Pr}\left[\mathcal{A}\left(\mathbb{G},q,g,g^a,g^b,g^{ab}\right)=1\right]\right|\le \mathrm{negl}(n)$$
也即
$$Adv\mathcal{A}\le \mathrm{negl}(n)$$
从而我们证明了：如果 DDH 问题是困难的, ElGamal加密方案在IND-CPA 安全模型下是安全的。

关于ElGamal、CDH、DDH

对于ElGamal的安全性分析有两种：一种是基于Random Oracle模型，使用了CDH假设；另一种，没有Random Oracle模型，但是使用更强的DDH假设。

Random Oracle

由此：如果DDH假设在G中为假，则假设CDH在G中成立，该方案仍然是安全的，但限制在在较弱的Random Oracle语义安全(Semantic Secure)模型中。事实上，我们拥有其它避开RandomOracle的方法：可以通过强于CDH，但弱于DDH的hash Diffie-Hellman (HDH)假设，来实现IND-CPA安全。

Further Study

更高的安全性：从CPA到CCA

安全目标

• 单向性（OW）安全: 由密文不能恢复相应的明文
• 不可区分性（IND）安全: 对已知给定的的两个明文，加密者随机一致的选择其中一个进行加密，攻击者无法从密文中知道是对哪个明文的加密。
• 非延展性（NM）安全: 攻止者无法构造与已给密文相关的新密文。
• NM > IND > OW

攻击模式

• 选择明文（CPA）攻击：攻击者可以先适应性选择明文， 获得相应的密文
• 非适应性选择密文（CCA1）攻击：攻击者除了可以适应性选择明文攻赤外，在给定Challenge密文前，还可以选择密文获得相应的解密。
• 适应性选择密文（CCA2）攻击：攻止者的唯一限制就是不可以直接用Challenge密文获得相应的明文，即还可以在给定Challenge密文，选择密文获得相应的解密。

研究进展

2001，Abdalla, Bellare, Rogway.提出的DHIES，将ElGamal加密转化为IND-CCA2，其效率非常高，不需要Random Oracle，其安全性基于 Oracle Diffie-Hellman假设。

DHIES Conference Paper