二叉树
1. 二叉树打印练习题
有一棵二叉树,请设计一个算法,按照层次打印这棵二叉树。给定二叉树的根结点root,请返回打印结果,结果按照每一层一个数组进行储存,所有数组的顺序按照层数从上往下,且每一层的数组内元素按照从左往右排列。保证结点数小于等于500。
# _*_ coding:utf8 _*_
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class TreePrinter:
def printTree(self,root):
#write code here
res=[]
if root==None:
return res
queue=[]
queue.append(root)
nlast=last=root
temp=[]
while len(queue):
node=queue.pop(0)
temp.append(node.val)
if node.left!=None:
queue.append(node.left)
nlast=node.left
if node.right!=None:
queue.append(node.right)
nlast=node.right
if node==last:
res.append(temp[:])
last=nlast
temp=[]
return res
字符串
1. 两串旋转练习题
如果对于一个字符串A,将A的前面任意一部分挪到后边去形成的字符串称为A的旋转词。比如A="12345",A的旋转词有"12345","23451","34512","45123"和"51234"。对于两个字符串A和B,请判断A和B是否互为旋转词。
给定两个字符串A和B及他们的长度lena,lenb,请返回一个bool值,代表他们是否互为旋转词。
测试样例:
"cdab",4,"abcd",4
返回:true
# -*- coding:utf-8 -*-
class Rotation:
def chkRotation(self, A, lena, B, lenb):
# write code here
if lena!=lenb: #先判断长度是否相同
return False
else:
string=A+A #判断B在A+A中是否出现,出现则时旋转词
if B in string:
return True
else:
return False
排序
冒泡排序_O(n^2)
原理:
第一趟,相邻元素比较,大的往下沉,最后一个元素最大;
第二趟,相邻元素比较,大的往下沉,最后一个元素不用比;
第三趟,相邻元素比较,大的往下沉,最后两个元素不用比;
...
直到最后只剩下一个元素,此时比较了n-1趟。
过程:
冒泡排序是两两相邻元素比较;一开始交换区间是0到N-1,也就是整个数组的整体,首先第一个元素与第二个元素比较,大的放后面,然后第二个元素与第三个元素比较,哪个大哪个就放在后面,这样依次交换过去,最大的数最终就会放在数组的最后面;然后进行第二轮比较,将交换区间变成0到N-2,一轮交换过后第二大的数就放在了数组倒数第二的位置;依次进行这样的交换过程,把范围从0到N-1最后变成只剩下一个元素的时候,整个数组就变得有序了。
1. 冒泡排序练习题
对于一个int数组,请编写一个冒泡排序算法,对数组元素排序。
给定一个int数组A及数组的大小n,请返回排序后的数组。
测试样例:
[1,2,3,5,2,3],6
[1,2,2,3,3,5]
# -*- coding:utf-8 -*-
class BubbleSort:
def bubbleSort(self, A, n):
# write code here
for i in range(n-1):
for j in range(n-1):
if A[j]>=A[j+1]:
A[j],A[j+1]=A[j+1],A[j]
#交换过程也可以写成:
#temp=A[j]
#A[j]=A[j+1]
#A[j+1]=temp
return A
选择排序_O(n^2)
原理:
每一次从待排序的数据元素中选出一个最小值,放到序列的起始位置,直到全部排完。
过程:
选择排序,一开始对整个数组0到N-1范围上,选出一个最小值,然后把它放在位置0上;然后在1到N-1的范围上,选出一个最小值把它放在位置1上;这样依次缩小范围,从0到N-1,2到N-1,3到N-1,直到最后只剩下一个数的时候(即范围只包含一个数的时候),整个数组就变得有序了。
选择排序练习题
对于一个int数组,请编写一个选择排序算法,对数组元素排序。
给定一个int数组A及数组的大小n,请返回排序后的数组。
测试样例:
[1,2,3,5,2,3],6
[1,2,2,3,3,5]
# -*- coding:utf-8 -*-
class SelectionSort:
def selectionSort(self, A, n):
# write code here
for i in range(n):
for j in range(i+1,n):
if A[j]插入排序_O(n^2)
原理:(相当于摸牌)
数组被分为有序区和无序区,开始有序区只有一个元素,从无序区取一个元素插入到有序区中,直到无序区变空。
过程:
首先位置1的元素与位置0的元素进行比较,如果位置1的数更小,则交换;然后位置2的数我们记为a,依次与前面的数,位置1,位置0的数进行比较,如果a比位置1上的数更小,则交换,交换之后a继续与位置0上的数比较,如果还是a更小,则与位置0上的数进行交换;对于位置k上的数,记为b,b就依次与前面的数进行比较,如果b一直小于它前面的数,就一直进行这样的交换过程,直到前面的数小于等于b,那么b就插入当前位置;这样依次将位置1到位置N-1的数进行这样的插入的过程,最终数组就变得有序了。
插入排序练习题
对于一个int数组,请编写一个插入排序算法,对数组元素排序。给定一个int数组A及数组的大小n,请返回排序后的数组。
测试样例:
[1,2,3,5,2,3],6
[1,2,2,3,3,5]
比较一次则插入一次:
# -*- coding:utf-8 -*-
class InsertionSort:
def insertionSort(self, A, n):
# write code here
for i in range(1,n): #手里已经有一张牌,待摸的牌从第二张开始到最后一张
key=A[i] #刚摸的牌
j=i-1 #手上最右一张牌
while j>=0: #直到比较到第一张牌则停止
if key比较完之后再插入:
# -*- coding:utf-8 -*-
class InsertionSort:
def insertionSort(self, A, n):
# write code here
for i in range(1,n): #手里已经有一张牌,待摸的牌从第二张开始到最后一张
key=A[i] #刚摸的牌
j=i-1#手上最右一张牌
while j>=0 and key归并排序_O(nlogn)
原理:
首先让数组中每个元素单独成为长度为1的有序区间,然后让相邻两个长度为1的有序区间合并,变成最大长度为2的有序区间,接下来再把相邻有序区间进行合并,得到最大长度为4的有序区间,依次这样进行下去,4合8,8合16,直到让数组中所有的数合并到一个统一的有序区间,整个数组变得有序了。
归并排序练习题
对于一个int数组,请编写一个归并排序算法,对数组元素排序。
给定一个int数组A及数组的大小n,请返回排序后的数组。
测试样例:
[1,2,3,5,2,3],6
[1,2,2,3,3,5]
# -*- coding:utf-8 -*-
class MergeSort:
def mergeSort(self, A, n):
# write code here
if n<=1:
return A
else:
mid=n/2
left=self.mergeSort(A[:mid],len(A[:mid])) #左边部分归并排序
right=self.mergeSort(A[mid:],len(A[mid:])) #右边部分归并排序
#此处注意不能使用mid代替len(A[:mid])或len(A[mid:]),因为n/2除法只取整数部分
return self.merge(left,right)
def merge(self,left,right): #归并排序过程
i,j=0,0
result=[]
while i 快速排序_O(nlogn)
原理:
随机的在数组中选一个数,小于等于它的数,统一地放在这个数的左边,大于它的数放在这个数的右边;接下来对左右两个部分,分别递归调用快速排序的过程,这样就使得整个数组都有序了。
划分过程_O(n):
随机在数组中选择一个划分值放在数组最后面,初始设置一个长度为0的小于等于区间放在数组的最左边,然后从左到右依次遍历数组的所有元素,若当前元素大于划分值,则继续遍历下一个元素,若当前元素小于等于划分值,则当前元素与小于等于区间的下一个元素进行交换,小于等于区间向右扩一个位置;直到遍历完所有的元素,我们把最后一个数即划分值,与小于等于区间下一个元素交换,这就是一个完整的划分过程。
快速排序练习题
对于一个int数组,请编写一个快速排序算法,对数组元素排序。
给定一个int数组A及数组的大小n,请返回排序后的数组。
测试样例:
[1,2,3,5,2,3],6
[1,2,2,3,3,5]
方法一:
# -*- coding:utf-8 -*-
class QuickSort:
def quickSort(self, A, n):
# write code here
return self.quick_Sort(A)
def quick_Sort(self,A):
if A==[]:
return A #若A是空list,则返回[]
else:
key=A[0] #取一个基准
left=self.quick_Sort([x for x in A[1:] if x < key]) #小于key的放到左边进行快排
right=self.quick_Sort([x for x in A[1:] if x >= key]) #小于key的放到右边进行快排
return left+[key]+right #key是一个数,变成list[key]再和list[left]和[right]拼接
方法二:
# -*- coding:utf-8 -*-
class QuickSort:
def quickSort(self, A, n):
# write code here
if n<1:
return A
else:
key=A[0] #设置基准
left=[] #设置左部分
right=[] #设置右部分
for x in A[1:]:
if x <=key:
left.append(x) #小于key的放左边
else:
right.append(x) #大于key的放右边
return self.quickSort(left,len(left))+[key]+self.quickSort(right,len(right))
#经过一次划分之后,分别对左右两部分进行快排
堆排序_O(nlogn)
原理:
将数组中的n个数建成一个大小为n的大根堆,我们知道堆顶是所有元素的最大值,把堆顶元素与堆的最后一个位置的数进行交换,然后将最大值脱离除整个堆结构,放在数组最后的位置;然后再把n-1个元素进行大根堆调整,堆顶元素与堆最后位置进行交换,得到n-1个元素中的最大值放到数组倒数第二个位置;这样依次将堆的大小从n减小到1,进行上面的过程,最终得到一个有序的数组。
希尔排序_O(nlogn)
原理:
其实是一个改良的插入排序算法,插入排序步长为1,希尔排序的步长是从大到小调整的,假设步长为n,数组前n为元素不需要考虑,从第n+1个元素开始,向前跳n位进行插入排序的过程,依次遍历所有元素,直到最后一个元素;然后调整步长为n-1,从第n个元素开始,向前跳n-1为进行插入排序过程,直到遍历到最后一个元素;这样依次调整步长从n到1的时候,这个数组就有序了。
算法题
1.Move zeros
将数组中的0移动到数组末端,如输入:(第一个输入是数组的长度)
4
3
2
0
9
输出:
3
2
9
0
- 这里注意输入换了行,输出也是。
方法一:
n = input()
data = []
for i in range(int(n)): #输入长度为int(n)的字符串,一个一个按行输入
temp = input()
data.append(int(temp))
num = data.count(0) #元素为0的数目
for i in range(num): #假如有4个0,则循环4次
index = data.index(0) #元素为0的索引
temp = data[index] #将0赋给temp
data[index:-1] = data[index+1:]
#将0之后的所有元素向前移动一位,注意list[0:-1],是从第一个元素到倒数第二个元素
data[-1] = temp #这里区分data[-1]指的是最后一个元素,data[:-1]是第一个元素到倒数第二个元素
for i in data: #按行打印出来
print(i)
方法二:
n = int(input())
data = []
for i in range(n):
a = input()
data.append(int(a))
def MoveZeros(data,n):
cur = 0 #当前索引从第一个元素开始
for i in range(n): #遍历所有元素
if data[i]:
data[cur], data[i] = data[i], data[cur]
#将不为0的元素放到已经遍历过的非0序列的最后边
cur += 1
return data
res=MoveZeros(data,n)
for i in res:
print(i)
2. 平方等式
输入k,a,b使得k*f(n)=n,计算有多少个这样的整数n,其中a<=n<=b,f(n)是这样一个函数:f(13)=1+9=10,f(24)=4+16=20
示例:
输入:
51 5000 10000
输出:
3
data=input()
data=data.strip().split(" ")
k=int(data[0])
a=int(data[1])
b=int(data[2])
count = 0
def f(n):
sum = 0
data=list(str(n)) #list()里面必须是string型
for i in data:
sum += int(i)**2
return sum
for n in range(a,b+1): #因为range里面的a,b必须是int型
if k*f(n)==n:
count +=1
print(count)
3. 单词缩写
在日常书面表达中,我们经常会碰到很长的单词,比如"localization"、"internationalization"等。为了书写方便,我们会将太长的单词进行缩写。这里进行如下定义:
如果一个单词包含的字符个数超过10则我们认为它是一个长单词。所有的长单词都需要进行缩写,缩写的方法是先写下这个单词的首尾字符,然后再在首尾字符中间写上这个单词去掉首尾字符后所包含的字符个数。比如"localization"缩写后得到的是"l10n","internationalization"缩写后得到的是"i18n"。现给出n个单词,将其中的长单词进行缩写,其余的按原样输出。
输入
第一行包含要给整数n。1≤n≤100
接下来n行每行包含一个由小写英文字符构成的字符串,字符串长度不超过100。
输出
按顺序输出处理后的每个单词。
样例输入
4
word
localization
internationalization
pneumonoultramicroscopicsilicovolcanoconiosis
样例输出
word
l10n
i18n
p43s
解答:
In [8]: n = input()
...: m=[]
...: if 1<=len(n)<=100:
...: for i in range(int(n)):
...: m.append(input())
...: for i in m:
...: if len(i) <=10:
...: print(i)
...: else:
...: print(i[0]+str(len(i)-2)+i[-1])
...:
...:
4
abcd
asdfgdaghgfhjdf
safasfdagf
asdghfdgdghdasfgag
abcd
a13f
safasfdagf
a16g
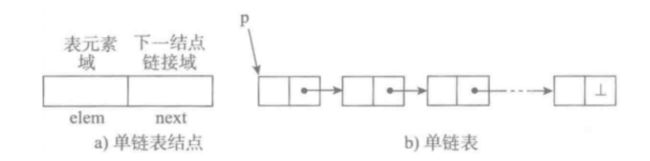
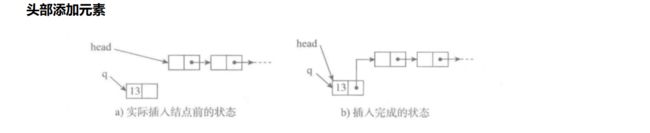
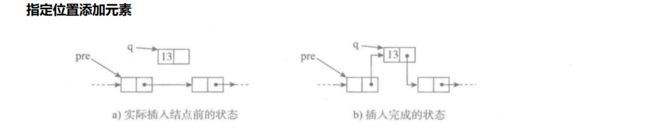
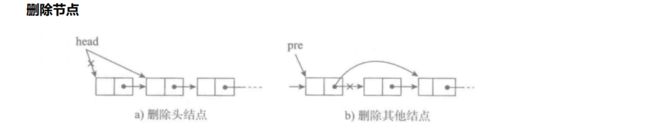
链表
[单向链表]
单向链表也叫单链表,是链表中最简单的一种形式,它的每个节点包含两个域,一个信息域(元素域)和一个链接域。这个链接指向链表中的下一个节点,而最后一个节点的链接域则指向一个空值。