二分查找算法的简单介绍
今天我们来学习一下二分查找算法,也叫做折半查找算法。使用二分查找算法的前提是数据需要是有序的。二分查找的思想非常简单,很容易理解,就是每次取中间位置的数和要找的数作比较,通过判断是大还是小来重新选择中间位置,直到找到。但是在实际的应用中却并不简单,因为我们实际碰到的问题不会像一个排好序的数组,然后让我们找出其中是不是包含某一个数这么简单。
简单的例子
我们在生活中也会经常遇到二分查找的使用,比如我们应该都玩过猜数字的游戏,我随便写一个 1 到 100 中间的数,然后你来猜我写的是多少,每次你猜之后我会告诉你是大了还是小了,直到你猜中为止。所有人都知道,我们每次都取中间数去猜,然后根据提示大了小了重新选择中间数,直到猜中。这样是速度最快的办法。这里我们用到的就是二分查找算法。
比如我写的数是 36,使用二分法的步骤就像下图展示的。
| 次数 | 猜测范围 | 中间数 | 比较 |
|---|---|---|---|
| 1 | 1-100 | 50 | 50>36 |
| 2 | 1-49 | 24 | 24<36 |
| 3 | 25-49 | 37 | 37>36 |
| 4 | 25-36 | 30 | 30<36 |
| 5 | 31-36 | 33 | 33<36 |
| 6 | 34-36 | 35 | 35<36 |
| 7 | 36 | ✔️ |
7 次就猜出来我写的数,还是很快的是吧。那如果最开始的范围是 1-1000 或者 1-10000 甚至更大的范围需要多少次呢?感兴趣的可以自己试试。
时间复杂度
我们通过上边简单的例子也了解了二分查找算法的原理和思想,下面我们来分析一下二分查找算法的时间复杂的。
我们假设数据的大小为 n,每次查找后数据都会变为原来的一半,也就是 n/2,然后直到找到最后要找的值,最坏的情况就是数据中没有我们要找的值,直到查找区间被缩小为空,才停止。
查找区间的大小变化:
| 次数 | 大小 |
|---|---|
| 0 | n |
| 1 | n/2 |
| 2 | n/4 |
| … | … |
| k | n/2^k |
| … | … |
最坏的情况就是 n/2^k = 1 的时候,k 就是总共缩小的次数,每次缩小我们只需要比较两个数的大小,所以,一共有 k 次比较,时间复杂度为 O(k)。
通过 n/2^k = 1,我们可以求得 k = log2(n),所以最后的时间复杂度为O(logn)。
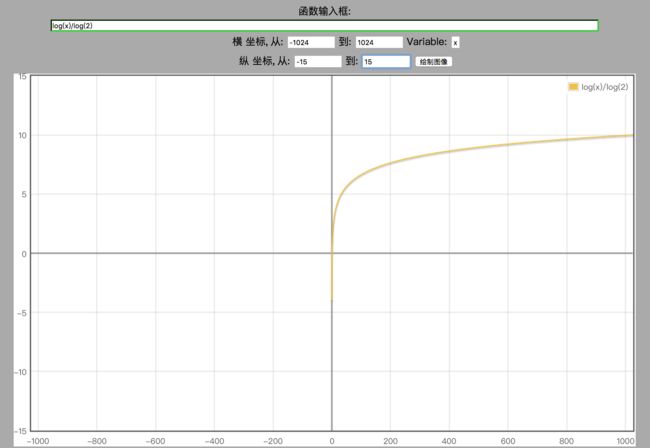
我们在深入的了解一下 O(logn) 这种时间复杂度。我们首先来看一下 logn 的函数的数学图像。
图1中横坐标的值是从 -1024 到 1024 ,而 y 的值最大也不过才是 10。
图2中横坐标的值时从 -4294967296 到 4294967296,也就是 -2^32 到 2^32 ,y 的最大值是 32 ,可见 x 都大到了四十多亿了,y 的值不过才32。可见二分查找在数据量是如此巨大的时候查找的次数也不过才几十次。所以说二分查找算法是非常高效的。
代码实现
我们已经了解了二分法的思想和查找过程。下面通过具体的代码来实现二分查找算法。
最简单的情况是已经排好序的没有重复元素的数组,然后我们找出数组中有没有与给定值相等的元素。
public int BinarySearch(int[] array,int n, int value){
int low = 0;
int high = n - 1;
while(low<=high){
int mid = (low + high) / 2;
if(array[mid] > value){
high = mid - 1;
}
else if(array[mid] > value){
low = mid + 1;
}
else{
return mid;
}
}
return -1;
}
当然,我们上边只是最简单一种情况,下面我们稍微增加一点难度。如果数组中有重复的元素的话。我们算法该怎么写呢?
- 查找第一个值等于给定值的元素
public int BinarySearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else if (a[mid] < value) {
low = mid + 1;
} else {
if ((mid == 0) || (a[mid - 1] != value)) return mid;
else high = mid - 1;
}
}
return -1;
}
我们判断 array[mid] 与给定值大小关系有大于小于和等于,当大于或小于的时候和最简单没有重复元素时候一样,只需要更新 high 和 low 的值就协议了。但当等于的时候,我们不能立马返回,因为我们不知道这个是不是第一个等于给定值的元素。所以我们要判断,如果 mid 等于 0 的话,是数组的第一个元素,那么肯定是第一个等于给定值的;如果 mid 不等于 0 ,我们查看前一个元素 array[mid-1] 的值如果不等于 value,那么 array[mid] 就是第一个等于 value 的值,如果前一个元素等于 value 的话,我们需要更新 high 的值,因为要找的元素肯定在 [low, mid-1]之间。
- 查找最后一个值等于给定值的元素
上边我们求得是第一个等于给定值的元素,这次我们来找最后一个。只需要将上边的代码稍微改动一下就可以了
public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else if (a[mid] < value) {
low = mid + 1;
} else {
if ((mid == n - 1) || (a[mid + 1] != value)) return mid;
else low = mid + 1;
}
}
return -1;
}
参照上边查找第一个等于给定值的讲解,这个也就很容易理解了。
- 查找第一个大于等于给定值的元素
在数组中,查找第一个大于等于给定值的元素,比如数组 [1,4,4,5,7,9],查找第一个大于等于 6 的元素,那就是 7。
public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] >= value) {
if ((mid == 0) || (a[mid - 1] < value)) return mid;
else high = mid - 1;
} else {
low = mid + 1;
}
}
return -1;
}
这个和第一个等于给定值的情况多了大于的条件,所以我们只需要把原来的等于的情况和大于的情况和到一起来判断就可以了
- 查找最后一个小于等于给定值的元素
public int bsearch7(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else {
if ((mid == n - 1) || (a[mid + 1] > value)) return mid;
else low = mid + 1;
}
}
return -1;
}
有了上边的做铺垫,这个应该很容易就理解了。这里就不做过多解释了。
总结一下
通过上边我们的代码的实例,总结出我们写二分查找算法时候需要注意的几个地方。
1、终止条件的正确性
2、区间上下界的更新
3、返回值的选择
注意到这几个条件后,我们写的算法应该就不容易有 bug 了。
虽然二分查找非常的简单高效,但也有它的局限性。
- 数据结构必须有序
二分查找要求数据是有序的,这样我们才能使用二分查找。 - 依赖的是顺序表结构
也就是数组,因为二分查找是通过下标来访问元素的,如果是链表的话,二分查找的时间复杂度就非常高了。 - 数据太小不适合
如果数据量很小,完全没必要使用二分法了,顺序遍历比较就可以了。 - 数据太大不适合
你上边不是说了二分法很适合用在大数据量的查找吗,而且越大的数据量越能体现二分查找算法的高效吗。为什么又不适合了呢。因为二分查找依赖于想数组这样的顺序表结构,而这种结构为了提供随机访问,要就内存空间是连续的。
也就是如果我们要处理 10G 的数据,我们需要 10G 的连续的内存空间,如果你内存还有很多,可都是不连续的,分散的,同样不能使用二分查找。