《520之前脱单》单身的兄弟们看这里教你如何快速找到女朋友并发生故事 当然是选动态规划呀 听说看完的人都脱单了
论如何快速在520之前找到女朋友并发生故事
不会吧 不会吧 不会到现在还有人没有脱单吧!别急,兄弟们,看完这篇文章你还找不多女朋友算我的。好啦,废话不多说,直接上干货。(前方高能,请注意,老铁们,稳住啊)

这样的女朋友兄弟们是不是很想要呀,小公举也很想要。那我们就一起火力全开去追吧。
我们来玩个小游戏,谁赢了就能把这个小姐姐抱回家好吗。游戏规则如下:

在上面的数字三角形中,假设漂亮小姐姐在最底层等你手牵手,那么你该如何寻找一条从顶部到底边的路径,使得路径上所经过的数字之和最大。路径上的每一步都只能往左下或 右下走。谁走的路程经过的数字之和最大,那么谁就能和小姐姐牵手,漂亮小姐姐就是你女朋友了。
那么,我们该如何走才能赢得女朋友呢。经过分析,我们不难发现,这适合用动态规划解决。
①最优子结构
假定我们要走到最底层,即从第n-1层走到第n层,那么第n-1层的每个结点我们只能往左下角或者右下角走,每个结点都是只能这样走。同样的,第n-2层走到n-1层也是这样,以此类推,我们发现了子问题有重叠子结构。
②递归定义最优值
因为到最后一层之后我们不用走了,所以最后一层的节点的最大路径和就是本身结点的权重,即dp[n][j]=b[n][j],其中b[i][j]代表每层每个节点的权重,dp[i][j]定义为最大路径和,所以可得递推方程为:
dp[i][j]=(max{dp[i+1][j],dp[i+1][j+1]}+b[i][j])
dp[i+1][j]是当前节点的左下角节点的最大路径和,dp[i+1][j+1]是当前节点的右下角节点的最大路径和。
③计算最优值
由于是自底向上方法求解问题,所以最终的最优值为dp[1][1]。
代码如下(java):
package 算法分析;
import java.util.*;
public class MathTriangle {
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
System.out.print("请输入三角形数字的行数:");
int m = s.nextInt(); //三角形行数
System.out.println("请输入每行的三角形数字:");
int [][]b = new int [m+1][m+1]; //存储每个点对应的数字
int [][]dp = new int [m+1][m+1]; //到每个点的最大值
for(int i=1;i<=m;i++) {
//初始化三角形数字
for(int j=1;j<=i;j++) {
b[i][j] = s.nextInt();
}
}
mathtriangle(m,dp,b); //计算最大值
}
//m是行数,dp存放到某个点的最大值,b存放三角形数字
public static void mathtriangle(int m,int [][]dp,int [][]b) {
for(int j=1;j<=m;j++) {
//初始化最后一行的最大值,因为最后一行
dp[m][j] = b[m][j];//没有继续往下的路径,所以最大值就是本身这个点所代表的的数字
}
for(int i=m-1;i>=1;i--) {
for(int j=1;j<=i;j++) {
if(dp[i+1][j]>dp[i+1][j+1]) {
//左下点到该点的距离比右下点到该点的距离大
dp[i][j] = dp[i+1][j] + b[i][j]; //则左下的长度+上该点的长度就是最大的
}else {
dp[i][j] = dp[i+1][j+1] + b[i][j];
}
}
}
//自底向上计算,所以最大值为dp[1][1]
System.out.println("最大值为:"+dp[1][1]);
}
}
运行结果如下:

看到这里,恭喜你呀,如意找到了漂亮的女朋友,以后记得多补补身体哈,别过度劳累了。看着来,兄弟们,不然吃不消的,帮兄弟找到女朋友了,那是不是该点个赞作为回报呢,为了你的女朋友可把我愁坏了
在你们相处一段时间之后,是不是该考虑带女朋友出去旅游一波了,而且这番旅游之后你们的回忆会有更多的美好故事。
那么你们去旅游,是不是要考虑一下要带哪些物品呀,比如化妆品,肾宝片等等,但是我们的背包容量又有限,那我们该怎么选择带什么物品才能使得所带的东西总价值最大呢?**注意,**物品是不能分割的哦,要么就带,要么就不带。
假设
现在有n个物品,c表示背包总容量,Wi表示第i个物品的重量,vi是第i个物品的价值,找出一个n元0-1向量(x1,x2,…,xn)xi=0表示不装入背包,xi=1表示装入背包,使得(i=1to n)wixi<=c,且vixi达到最大。也就是在背包容量为c的情况下带哪些物品才能使得总的价值最大呢
①最优子结构
设(y1,y2,…,yn)是所给的一个最优解,则(y2,y3,…,yn)是下面相应子问题的一个最优解。
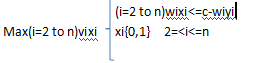
②递归定义最优值
设j 表示当前背包剩余容量,m(i,j)表示在背包可用容量为j,待考虑装入包的物品集为(1,2,…,i)时的最大装入物品价值,则m(n,c)表示原问题的最优解,即背包的最大价值。
那么,我们装入第i个物品时,有如下三种可能:
若j
若j>=wi,且装入第i件物品后的价值比不装入的价值大,那么最大价值要改变。所以得:

③计算最优值
M(n,c) 表示原问题最大价值,n是物品个数,c是背包总容量。
④构造最优解
用x数组记录最优解,自底向上求解,如果m[i][c]==m[i-1][c],那么第i件物品不放入,置x[i]=0;如果m[i][c]!=m[i-1][c],那么第i件物品放入背包,置x[i]=1。最后根据x[i]=1输出构成最优解的物品。
举例说明:

实验代码如下(java):
package 算法分析;
import java.util.*;
public class KnaPack {
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
int M,N; //分别是商品个数和背包容量
System.out.print("请输入商品个数: ");
M = s.nextInt();
System.out.print("请输入背包最大容量: ");
N = s.nextInt();
int []x = new int [M+1]; //记录构成最大价值的物品
int []w = new int [M+1]; //物品对应的重量
int []v = new int [M+1]; //物品对应的价值
int [][]m = new int [M+1][N+1];
System.out.println("请分别输入物品的重量:");
for(int i=1;i<w.length;i++) {
w[i] = s.nextInt();
}
System.out.println("请分别输入物品的价值:");
for(int i=1;i<v.length;i++) {
v[i] = s.nextInt();
}
knapsack(M,N,w,v,m); //计算最大价值
System.out.println("以下序号的商品构成的价值最大:");
traceback(M,N,w,m,x); //输出构成最大价值的商品
}
//求最大价值
//MN分别是商品个数和背包总容量,w是物品重量,v是物品价值,m最优值
public static void knapsack(int M,int N,int []w,int []v,int [][]m) {
for(int i=1;i<=M;i++) {
for(int j=1;j<=N;j++) {
//j表示当前背包的剩余容量
//背包剩余容量如果小于将要放入背包的物品的重量
//或者放入物品后背包的价值比不放入还小,则不改变最大价值
if(j<w[i] || m[i-1][j] > (m[i-1][j-w[i]]+v[i])) {
m[i][j] = m[i-1][j];
}else {
m[i][j] = m[i-1][j-w[i]]+v[i];
}
}
}
System.out.println("最大价值为:"+m[M][N]);
}
//求构成最大价值的物品
public static void traceback(int M,int N,int []w,int [][]m,int []x) {
for(int i=M;i>1;i--) {
if(m[i][N]==m[i-1][N]) {
x[i] = 0;
}else {
x[i] = 1;
N = N-w[i];
}
}
if(N>w[1]) {
x[1] = 1;
}
for(int i=1;i<=M;i++) {
if(x[i]==1) {
System.out.print(i+" ");
}
}
}
}
运行结果如下

小公举连夜帮兄弟们选择出最大价值的物品了,比如肾宝片这些必带的,那是不是该点赞+收藏+评论呢
你以为这样就完了?还有必杀技没亮出来呢?
大家都知道,和女朋友出去旅游肯定少不了花钱的,但是我们该怎样才能做到花最少的钱达到最大的效果,收货最大的快乐呢?小公举也给兄弟们整理出来了,请往下看。
假如:
你女朋友穿着比基尼和你在沙滩上玩,然后突然她想去海里的一个宝岛玩,但是要坐游艇。沙滩离宝岛有n个游艇出租站1,2,…n,你们可在这些游艇出租站租用游艇,并在往后的任何一个游艇出租站归还游艇。游艇出租站i到游艇出租站j之间的租金为r(i,j) ,1<=i 我们用m[i][j]表示从第i站到j站所需的最少租金。从i站到j站,我们可以从中间划分分两部分,即i到k,k到j站,寻找如何划分才能使租金最少。我们知道: 看在小公举熬夜加班给兄弟们做出了一份精华,从追女朋友到和女朋友出去旅游如何选择带价值最大的物品再到如何花费最少的钱和女朋友玩却有美好的故事发生,小公举可是把白头发都熬出来了,比兄弟们晚上二人世界还累呢,所以是不是该点赞+评论+收藏+打赏+分享呢,听说点赞+评论+收藏+打赏+分享的兄弟们都会在520之前脱单 【无名之辈我是谁 小小的天 也有大大的梦想】 我的梦想就是帮兄弟们实现赶在520脱单的梦想。
如果i=j 则不用租金,即m[i][j]=0
如果i!=j,则考虑i直接到j和划分之后哪种方式所需租金最少,即m[i][j]=min{m[i][k]+m[k][j]}. 最后得到的m[1][n]就是最优值,即从第1站到第n站的最少租金。
举例说明:

代码如下(java):
package 算法分析;
import java.util.*;
public class MinPrice {
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
System.out.print("请输入站数:");
int n = s.nextInt();
int [][]m = new int [n+1][n+1];
System.out.println("下面"+(n-1)+"行分别是第i站到第j站的租金");
for(int i=1;i<m[0].length;i++) {
for(int j=i+1;j<m[0].length;j++) {
m[i][j] = s.nextInt();
}
}
minprice(m);
}
//求最小值
public static void minprice(int [][]m) {
int i = 0,j = 0;
for(int len=2;len<m[0].length;len++) {
//区间长度
for(i=1;i<m[0].length-len+1;i++) {
//起点
j=i+len-1; //终点
for(int k=i+1;k<j;k++) {
//过程点
if(m[i][k]+m[k][j] < m[i][j]) {
m[i][j] = m[i][k]+m[k][j];
}
}
}
}
System.out.println("最小租金是:"+m[1][m[0].length-1]);
}
}
运行结果如下所示:

好了,小公举连夜加班送兄弟们上岛了,剩下的就交给各位兄弟了,毕竟岛上发生的羞羞射射的事情是由你们去创造的。温馨提示,记得带好晚上那些事情的必需品哦,小公举就不打扰你们的二人世界了。
