广州大学ACM2021第11周训练2021.05.16

广州大学ACM2021第11周训练

闲话：很久没打周赛了（其实是没有），五个小时上线了三个小时，整体来说前面五题都很简单，不过在细节处一直没处理好，很考验心态。最后是a4题，第五题读完题就有事跑路了，不过也是道暴力枚举题，稍微二进制压缩一下而已。

A - 交易 Gym - 102890I

题意

大致意思是要去买三本书（一开始读成n本书），给出了价格，可以根据需要组合起来去付款，这里有个优惠，就是满500减100。

题解

既然题目说满500减100，那么久尽量去凑多组500以上的，我们可以先排序，然后从小到大组一组记录价格总和，当和大于等于500时就可以将它们分成一组。因为这里只有三本书，所以很简单就算枚举也能过，这里的方法应该是使用于n的。

code

using namespace std;
const int N=1e5;
int a[N];
int main()
{
     
    //IOS
    int d;
    int cnt=0;
    while(cin>>d){
     
        a[cnt++]=d;
    }
    sort(a,a+cnt);
    ll ans=0;
    int i=0;
    ll t=0;
    for(;i<cnt&&a[i]<500;i++){
     
        t+=a[i];
        if(t>=500){
     
            ans+=(t-100);t=0;
        }
    }
    if(t>0){
     
        ans+=t;
    }
    for(;i<cnt;i++)ans+=(a[i]-100);
    cout<<ans<<'\n';
    return 0;
}

B - 三角形 Gym - 102890C

题意

题目要求数三角形。原本有一个大三角形，现在在由往下切n条线，再平行于地面切k条线，问此时能包含的不同三角形有多少个。一共t组样例。

题解

首先容易发现，三角形一个顶点是确定的，平行切了k刀，那么数的时候就要遍历底边，所以这里是k+1条底边，而每一边的情况是相同的，也就是说数出其中一种然后乘上k+1。
对于每组边，切n刀分成了n+1个小三角形，相邻若干个小三角形可以组成一个大点的三角形，所以从三角形大小入手，应该有n+1，n，n-1，~~，一直加到n-p=0，也就是最大的那个三角形，即n+1个组成的。很显然就是等差数列1加到n+1。答案再乘上上面说的k+1即可。
这里wa很很多遍，因为注意到答案要mod1e7，而我在计算等差数列时把/2放在了最后去计算，这完全是画蛇添足。因为等差数列结果（容易发现一定是奇数乘以偶数）取了模，所以它的奇偶性改变了，之后再去/2，那么就会有误差了，应该老老实实/2再去取模的。

code

using namespace std;
const int N=1e5;
const ll mod=1000000007;
int a[N];
int main()
{
     
    //IOS
    int t;cin>>t;
    while(t--)
    {
     
        ll n,k;
        cin>>k>>n;
        ll ans=(((k+1)*(k+2)/2)%mod*(n+1))%mod;
        cout<<ans<<'\n';
    }
    return 0;
}

C - 算式 AtCoder - arc061_a

题意

给你一个只含 1 ~ 9 的 字符串s，字符串的长度小于10。你可以在任意两个字母之间插入“+”使得其成为一个合法的算式，可以一个“+”号都不插入，问你所有合法 算式 的总和.

题解

字符串很短，暴力枚举每个地方加不加加号即可。枚举时可以二进制压缩一下。

code

using namespace std;
const int N=122;
const ll mod=1000000007;
ll dp[12][12];
int main()
{
     
    //IOS
    string s;cin>>s;
    int len=s.length();
    ll ans=0;
    ll now=0;
    for(int i=0;i<(1<<len-1);i++){
     
        now=0;
        for(int j=0;j<len;j++){
     
            now=now*10+s[j]-'0';
            if(j==len-1||(1<<j)&i){
     
                ans+=now;
                now=0;
            }
        }
    }
    cout<<ans<<'\n';
    return 0;
}

D - 通信网络 Gym - 102890D

题意

要求翻译字符串，并且给出一个最大长度，超过了这个长度就是不合法的。
至于字符串格式，就是数字加字母表示该字母有多少个，只有小写字母并且一个时可以省去数字。

题解

没什么好说的，模拟即可。

code

using namespace std;
const int N=1e5;
const ll mod=1000000007;
int a[N];
int main()
{
     
    //IOS
    int t;cin>>t;
    while(t--){
     
        string s;cin>>s;
        int maxn;cin>>maxn;
        string ans;
        int len=s.length();
        int p=1;
        bool yes=1;
        ll all=0;
        for(int i=0;i<len;){
     
            if(s[i]>='a'&&s[i]<='z'){
     
                ans+=s[i];
                all++;
                i++;
            }
            else {
     
                int j=i;
                string temp;
                temp+=s[j++];
                while(s[j]>='0'&&s[j]<='9')temp+=s[j],j++;
                ll o=atoi(temp.c_str());
                all+=o;
                if(all>maxn){
     yes=0;break;}
                while(o--)ans+=s[j];
                i=j+1;
            }
            if(yes==0)break;
        }
        if(all>maxn||(s[len-1]>='0'&&s[len-1]<='9'))yes=0;
        if(yes==0)cout<<"unfeasible\n";
        else if(yes==1)cout<<ans<<'\n';
    }
    return 0;
}

E - 计算单词 Gym - 102890L

题意

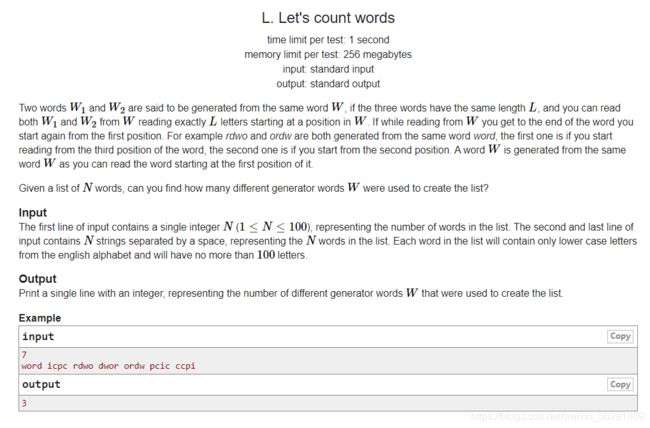
给出一个“子串”和“父串”的规则，即“子串”为“父串”无限循环后的子串。现给n个串，求出不同的“父串数量”。

题解

在判断归属关系时可以把父串拼接两边。先让答案对于n（视为每个串都是不相干的），遍历每个串，它与后面的串去比较，找到一个可以当它父串的，就让答案减1（这个串不是父传所以减掉），结束匹配（因为找到了就足够了）。

code

using namespace std;
const int N=122;
const ll mod=1000000007;
pair<string,string>all[N];
int yes[N];
int main()
{
     
    //IOS
    int n;cin>>n;
    for(int i=1;i<=n;i++){
     
        string t;cin>>t;
        string tt;tt=t+t+t;
        all[i]=make_pair(t,tt);
    }
    ll ans=n;
    for(int i=1;i<=n;i++){
     
        for(int j=i+1;j<=n;j++){
     
            if(all[j].first.length()==all[i].first.length()&&all[j].second.find(all[i].first)!=string::npos){
     
               ans--;
               break;
            }
        }
    }
    cout<<ans<<'\n';
    return 0;
}

G - 选手 Gym - 102890K

题意

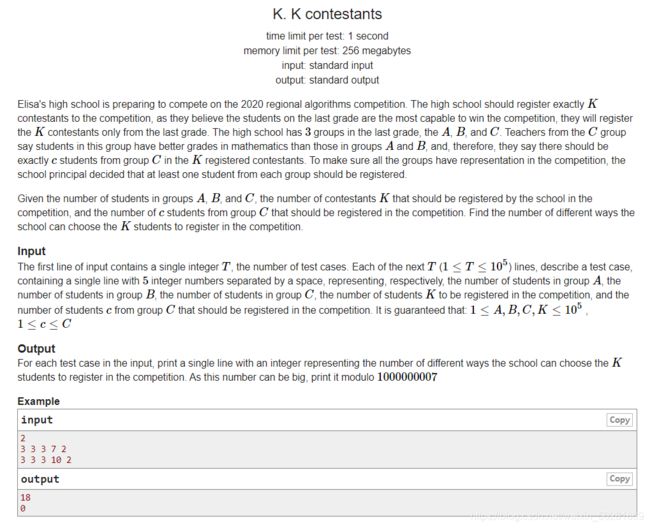
三组ABC各有一定人数，选出共k个人，C一定要选c个人，AB都得选至少一人。求选择方案数。结果对1e7取模。

题解

题目转为从C个人中选c个，A，B中选K-c个人，A，B至少选一个人的方案数。考虑直接组合数计算，然后减去A选K-c和B选K-c的方案数。（去掉A或B选不到一个人的情况）
注意先判断一下合理性。（选完c剩不到两个人）
这题难在组合数，因为结果要取模，如果按照有除法的方法可能存在除以0的情况。所以要换一种。
求组合数的方法有很多种，可以看这里。
因为有多组所以先预处理一下。

code

using namespace std;
const int N=2e5+2;
const ll mod=1000000007;
ll jie[N];
ll tow[N];
ll power(ll a,ll b,ll p)  //return a^b mod p
{
     
    ll temp = 1;
    while(b)
    {
     
        if(b & 0x01)
        {
     
            temp = (temp * (a%p)) % p;
        }
        a = ( (a%p) * (a%p) ) % p;
        b >>= 1;
    }
    return temp%p;
}
void init()
{
     
    jie[0]=1;
    for(int i=1;i<N;i++)jie[i]=jie[i-1]*i%mod;
    tow[N-1]=power(jie[N-1],mod-2,mod);
    for(int i=N-2;i>=0;i--) tow[i]=tow[i+1]*(i+1)%mod;
}
ll cal(ll n,ll m)
{
     
    if(m>n) return 0;
    return jie[n]*tow[m]%mod*tow[n-m]%mod;
}

int main()
{
     
    //IOS
    init();
    int t;cin>>t;
    while(t--){
     
        ll A,B,C,k,c;
        ll ans=0;
        cin>>A>>B>>C>>k>>c;
        if(k-c<2){
     cout<<0<<'\n';continue;}
        ll p=k-c;
        ll o=cal(A,p)+cal(B,p);o%=mod;
        ans=cal(A+B,p)-o+mod;
        ans%=mod;
        ans*=cal(C,c);
        ans%=mod;
        cout<<ans<<'\n';
    }
    return 0;
}

下面的题没读，都是有点难度的题（也有裸题），没读就不写了。