单因素方差分析与均匀性检验

ANOVA 均匀性检验代码展示

单因子方差分析

为了调查 1.5 V 3 号干电池的寿命是否由于生产工具的不同而不同，将每个厂的产品各取 5 个，测定其寿命，结果如下：

生产工厂	寿命	寿命	寿命	寿命	寿命
A1	24.7	24.3	21.6	19.3	20.3
A2	30.8	19.0	18.8	29.7	25.1
A3	17.9	30.4	34.9	34.1	15.9
A4	23.1	33.0	23.0	25.4	18.1
A5	25.2	37.5	31.6	26.8	27.5

对于同一个工厂生产的电池来说，他的寿命是一个随机变量。由于同一个工厂生产出来的产品大致相当，误差应服从正态分布，故随机变量也服从正态分布，即$X\sim N(\mu ,{\sigma }^2)$。所以，对于 $A1\sim A5$ 来说，他们的产品都服从正态分布 $X_i\sim N({\mu }_i,{\sigma }^2)$。但有一个重要前提，是他们的方差要相同，否则无法进行单因素方差分析。

单因素方差分析的原假设为 $H_0:{\mu }_1={\mu }_2=\cdots ={\mu }_n$，其中 $n$ 为工厂的数量。一般地，我们将影响因素成为因子或因素（factor），就本例而言，影响因素是工厂“类型”。

所以，单因素方差分析，就是为了判断类别型的自变量，对某个数量型的因变量有无影响的判断，且原假设是倾向于没有影响。

为了判断原假设，需要制定检验统计量。若原假设成立，我们有理由认为，每个样品，无论其生产工厂是谁，它们与其样本均值相差都不会太大，即：
$$S_s=\sum (x_{ij}-\bar{x}{)}^2$$
其中 $x_{ij}$ 是第 $i,i\in \{1,2,\cdots ,n\}$ 家工厂生产的第 $j,j\in \{1,2,\cdots ,n_i\}$ 个样品。$\bar{x}$ 是所有样品的均值：
$$\bar{x}=\sum _i^n\sum _j^{n_i}{x}_{ij}/\sum _i^n{n}_i$$

由于 $S_s$ 从统计学的角度，无法找出一个合适的分布，但考虑到：
$$\begin{array}{rl}{S}_s& =\sum _i^n\sum _j^{n_i}(x_{ij}-\bar{x}{)}^2\\ & =\sum _i^n\sum _j^{n_i}({\bar{x}}_i-\bar{x}{)}^2+\sum _i^n\sum _j^{n_i}(x_{ij}-{\bar{x}}_i{)}^2\end{array}$$
仔细观察上式，会发现第一项是属于同一个工厂的产品与其均值的差别，是同一个工厂（因素）的方差，我们可以称之为组内方差；第二项是每一个工厂的均值，与总均值之间的差别，是不同工厂的方差，我们称之为组间误差。于是我们可以把上式改写为：
$$S_s=S{S}_1+S{S}_2$$

而我们知道，若不同厂家生产出来的产品如果没有显著差异，那么式：
$$\frac{S{S}_1}{S{S}_2}$$
应该比较小。也即组间方差，比组内方差会比较小。

但是 $\frac{S{S}_1}{S{S}_2}$ 似乎没有一个特定的分布。但我们知道 $S{S}_1$ 在 $X_i\sim N({\mu }_i,{\sigma }^2)$ 时，满足$S{S}_1\sim {\chi }^2(n-1)$。令 ${\sum }_j{n}_j=m$，即样品总量记为 $m$，则 $S{S}_2$ 在 $X_i\sim N({\mu }_i,{\sigma }^2)$ 时，满足 $S{S}_2\sim {\chi }^2(m-n)$。 所以 $\frac{S{S}_1/(n-1)}{S{S}_2/(m-n)}$ 服从 F 分布：
$$F=\frac{S{S}_1/(n-1)}{S{S}_2/(m-n)}\sim F(n-1,m-n)$$
我们也称 $F$ 为检验统计量。

于是，以上述工厂-电池寿命为例，可算出 $F=1.17$

而在检验水平为 0.05 的情况下，F 分布在自由度为（4,20）的临界值为 2.866。于是，接受原假设，即可以认为工厂的规格，生产的电池的寿命没有影响。

均匀性检验

均匀性检验在 允差无法获取的情况下，一般会采用 ANOVA 进行。此时，一般会对多个样品（全检）测试至少 2 次以上。这时候，样品就是一个因素，相当于工厂，检测得到的多个值，就相当于工厂生产的电池。

均匀性是检验不同样品，是否“相同”， 换到 ANOVA，就是样品的种类，会不会导致不用样品的测试值有较大差异。

为什么可以用 ANOVA 呢？第一是因为正态性可以满足，对一个样品的测试值是一个随机变量，其分布取决于仪器的误差，误差一般可以认为是服从正态分布的，故满足正态性；其二，由同一厂家生产的样品，其方差肯定是相同的，满足方差齐性；均匀性检验的重复性，决定了测试数据的独立性，故可以使用 ANOVA。

以 CNAS-GL003 给出的例子为了：

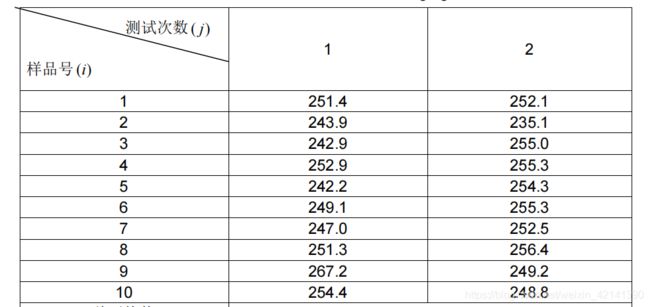
算出方差分析表，如下所示：

F 的计算值小于临界值，故可认为是均匀的。

代码

# -*- coding: utf-8 -*-
import pandas as pd
import numpy as np
from scipy.stats import f
import xlsxwriter

file_path = r'../附件/食用油BHA.xlsx'
X = pd.read_excel(file_path)

def anova(X, alpha=0.05, test_along_row=True, verbose=True):
    '''
    若 test_along_row 意味着对同一个水平的测试是分布在行上的。
    例如，若 test_along_row = True：
    则表格的表头大致如下：
    水平（样品号）： 测试1、测试2、测试3、...、测试 n
    '''
    
    X.drop(columns=X.columns[0], axis=1, inplace=True)
    
    rows, columns = X.shape
    # 样本容量
    m = rows*columns
    
    # 组内方差
    SS2 = 0
    # 组间方差
    SS1 = 0
    # 总均值
    bar_bar_x = 0
    bar_x = []
    for i in range(rows):
        # 求组内样品均值
        x_ij = X.iloc[i, :].values
        bar_x_i= x_ij.mean()  
        # 组内方差
        SS2 += np.square((x_ij-bar_x_i)).sum()
        # 总均值
        bar_x.append(bar_x_i)

    # 将 list 转换为 np.array
    bar_x = np.array(bar_x)
    bar_bar_x = bar_x.mean()
    # 求组间方差
    SS1 = columns*np.square((bar_x - bar_bar_x)).sum()
    # 组间自由度
    dfn = rows-1
    # 组内自由度
    dfd = m-rows
    # 求组间均方
    MS1 = SS1/dfn
    # 求组内均方
    MS2 = SS2/dfd
    # 检验统计量 F
    F = MS1/MS2
    # F 在 p=0.95 时的值
    F_alpha = f.ppf(1-alpha, dfn, dfd)
    
    if verbose:
    # 如果不愿输出 Excel 表格，可以将 verbose 设置为 False
        workbook = xlsxwriter.Workbook(r'../附件/ANOVA 结果.xlsx')
        worksheet = workbook.add_worksheet()

        cell_format = workbook.add_format()
        cell_format.set_border()
        cell_format.set_align('center')
        cell_format.set_align('vcenter')

        data_A = ['方差来源', '样品间', '样品内']
        data_B = ['自由度', dfn, dfd]
        data_C = ['平方和', SS1, SS2]
        data_D = ['均方', MS1, MS2]
        data_E = ['F', F]
        # 构造表格
        for i in ['A', 'B', 'C', 'D', 'E']:
            data = vars()[f'data_{i}']
            worksheet.write_column(f'{i}1', data, cell_format)

        workbook.close()
    
    text = r'''
        显著水平为{alpha}, 临界值为 F={F_alpha}
    '''.format(alpha=alpha, F_alpha=F_alpha)
    
    
    if F<F_alpha:
        text += '''
        F 的计算值为 {F} < F 临界值，这表明在{alpha}显著水平下，样本是均匀的。
        '''.format(F=F, alpha=alpha)
        print(text)
    else:
        text  += '''
        F 的计算值为 {F} > F 临界值，这表明在{alpha}显著水平下，样本不通过均匀性检验。
        '''.format(F=F, alpha=alpha)
        print(text)
    
    return F, MS1, MS2, dfn, dfd, bar_bar_x, F_alpha


F, MS1, MS2, dfn, dfd, bar_bar_x, F_alpha = anova(X, test_along_row=True)