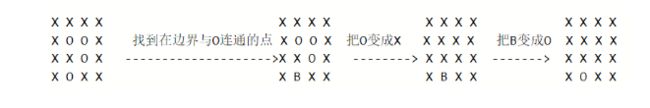Leetcode广度/深度遍历问题
目录
网格类问题DFS
200. 岛屿数量
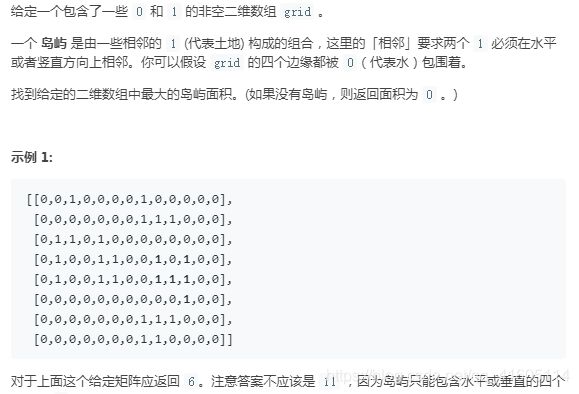
695. 岛屿的最大面积
463. 岛屿的周长
面试题12. 矩阵中的路径
网格类问题BFS
面试题13. 机器人的运动范围
综合题目
130. 被围绕的区域
827. 最大人工岛
有向无环图
207. 课程表
210. 课程表 II
1462. 课程安排 IV
广度优先遍历
127. 单词接龙
网格类问题DFS
参考内容:
https://leetcode-cn.com/problems/number-of-islands/solution/dao-yu-lei-wen-ti-de-tong-yong-jie-fa-dfs-bian-li-/
网格类DFS模板(C++版本):
动态规划和回溯法也有类似的题目,但是动态规划一般都是有始有终,回溯法基本就是N皇后类型的问题。
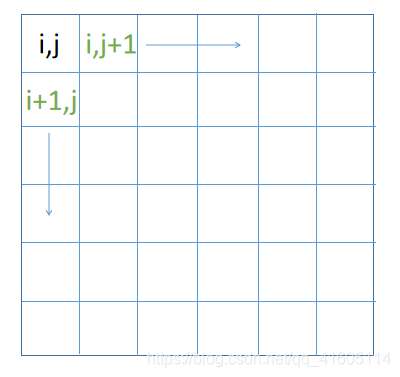
在这种网格中,完成点i,j的相关操作后,有周边的四个位置决定可以选择进行下一步操作,这相当于一个四叉树。
那么我们每次操作完一个点后,就有四种选择,我们需要全部遍历,和数的DFS性质一样,下面看模板:
void dfs(vector>& grid, int r, int c) {
if(!inArea(r,c)) return false;//判断该点是否在要求范围内
if(!isValid(r,c)) return false;//判断该点是否是有效点
//要避免重复访问一个点,所以在访问完一个点后,需要更改该点状态,表示该点已经被访问
dfs(grid, r - 1, c);
dfs(grid, r + 1, c);
dfs(grid, r, c - 1);
dfs(grid, r, c + 1);
} 下面我们来看相关题目:
200. 岛屿数量
https://leetcode-cn.com/problems/number-of-islands/
典型的网格DFS,那么我们套用模板
class Solution {
public:
int numIslands(vector>& grid) {
if(grid.empty()) return 0;
//规定不同的出发点
int row = grid.size(),col = grid[0].size();
int MAX = 0;
for(int i = 0;i>& grid)
{
int row = grid.size(),col = grid[0].size();
if(brow<0||brow>row-1||bcol<0||bcol>col-1) return false;
bool Res = false;
//此处需要标记哪儿些位置是你走过的
if(grid[brow][bcol] == '1') {Res = true;grid[brow][bcol] = 'x';}
else return Res;
//此处需要单独算,不能一起或到底,因为||是运算机制,会省略一些内容不算
bool N1 = DFS(brow-1,bcol,grid);
bool N2 = DFS(brow+1,bcol,grid);
bool N3 = DFS(brow,bcol-1,grid);
bool N4 = DFS(brow,bcol+1,grid);
return Res||N1||N2||N3||N4;
}
}; 参考官方解法。
我们遍历整个网格的所有部分,一旦找到岛屿,那么就展开DFS,然后标记从该点出发,能够到达的所有岛屿,让其失效,然后返回。网格的遍历工作继续,如果没有找到有效点,说明岛屿只有一个,如果找到了有效点,那么继续如法炮制即可。
695. 岛屿的最大面积
https://leetcode-cn.com/problems/max-area-of-island/
万变不离其宗,就是要求千变万化,整个遍历的方法还是保持一致,我们只是需要记录每次找到岛屿后,遍历过的点就好。
class Solution {
public:
int nums = 0;
int maxAreaOfIsland(vector>& grid) {
if(grid.empty()) return 0;
int row = grid.size(),col = grid[0].size();
int MAX = 0;
for(int i = 0;i>& grid,int r,int c)
{
if(grid[r][c] != 1) return;//无效点
int row = grid.size(),col = grid[0].size();
grid[r][c] = 2;//已经访问
nums++;
if(r-1>=0) dfs(grid,r-1,c);
if(r+1<=row-1) dfs(grid,r+1,c);
if(c-1>=0) dfs(grid,r,c-1);
if(c+1<=col-1) dfs(grid,r,c+1);
}
};
463. 岛屿的周长
https://leetcode-cn.com/problems/island-perimeter/
class Solution {
public:
int Res;
int islandPerimeter(vector>& grid) {
if(grid.empty()) return 0;
int row = grid.size(),col = grid[0].size();
int Res = 0;
for(int i = 0;i>& grid,int r,int c)
{
int row = grid.size(),col = grid[0].size();
if(r<0||c<0||r>=row||c>=col) return 1;//出界也算1
if(grid[r][c] == 0) return 1;//无效点,和海衔接,所以是1
if(grid[r][c] == 2) return 0;//无效点,访问过来所以是0
// int row = grid.size(),col = grid[0].size();
//已经访问过得点标记为2
grid[r][c] = 2;//要考虑已经走过的点
return dfs(grid, r - 1, c)+dfs(grid, r + 1, c)+dfs(grid, r, c - 1)+dfs(grid, r, c + 1);
}
};
类似问题:
此题细节很多,可以说是回溯法的变体,也可以说是DFS的变体
面试题12. 矩阵中的路径
https://leetcode-cn.com/problems/ju-zhen-zhong-de-lu-jing-lcof/
79. 单词搜索 https://leetcode-cn.com/problems/word-search/
回溯法:
有了N皇后的铺垫,这道题也就很好理解了,我们还是一个一个的去实验,题目要求起点任意,那么我们就在让每个位置都作为起点,进行实验。
从一个位置到另外一个位置,其实只需要有限个结果,不考虑重复,不考虑出界,最多四个结果,及上下左右
那么我们就设置一个索引量,表示目前要找第几个目标值,初始值为0,表示我们要找word中的第一个数字A,找到A之后,就要去找B,以此类推。
DFS:
我们从头遍历,以每个元素为起点进行DFS遍历,找出路径即可。
两种思路都是可以的,那么本题有什么细节要注意呢?
- 一旦找完,立即停止,及if(index == word.size()-1) return true;//完全找完,返回 (1)
- 探索完路径后,需要将改变标志的内容变回原来的样子;
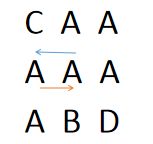
举例:
[["C","A","A"],["A","A","A"],["B","C","D"]] "AAB"
当我们从i = 1,j = 1为起点开始访问的时候,右侧是正确的路径,此时一定要标记该点为已经访问,否则i = 2,j = 0的点在DFS的时候也会再次访问该点,直接无限循环。
那么在访问结束一定要把该点的元素解除标记,否则只能遍历一次,全部都会变成已经访问过的点。这个一定要注意。
下面来看完整版代码:
class Solution {
public:
bool exist(vector>& board, string word) {
int row = board.size(), col = board[0].size();
for(int i = 0;i>& board, string word,int r,int c,int index)
{
int row = board.size(), col = board[0].size();
if(r<0||c<0||r>=row||c>=col) return false;//出界没找到
if(board[r][c] != word[index]) return false;//不等于
if(index == word.size()-1) return true;//完全找完,返回 (1)
char temp = board[r][c];
board[r][c] = '0';//标记已经访问的点,很重要
index++;//找下一个
bool Res = dfs(board,word,r-1,c,index)||dfs(board,word,r+1,c,index)||dfs(board,word,r,c-1,index)||dfs(board,word,r,c+1,index);
board[r][c] = temp;
return Res;
}
}; 329. 矩阵中的最长递增路径 https://leetcode-cn.com/problems/longest-increasing-path-in-a-matrix/
本题只要能想到使用DFS,就不是难题,难在记忆化递归上,不使用记忆化,会超时
class Solution {
public:
int longestIncreasingPath(vector< vector > &matrix) {
if(matrix.empty()) return 0;
int row = matrix.size(),col = matrix[0].size();
int MAX = 0;
//记忆化
vector>memo(row,vector(col,0));
for(int i = 0;i > &matrix,vector< vector > &memo,int i,int j,int Old){
int row = matrix.size(),col = matrix[0].size();
if(i<0||i>=row||j<0||j>=col||matrix[i][j]<=Old) return 0;
if(memo[i][j] > 0) return memo[i][j];
Old = matrix[i][j];
memo[i][j]++;
memo[i][j] += max(DFS(matrix,memo,i+1,j,Old),max(DFS(matrix,memo,i-1,j,Old),max(DFS(matrix,memo,i,j+1,Old),DFS(matrix,memo,i,j-1,Old))));
return memo[i][j];
}
}; 每个点的最长升序路径是固定的,计算过的地方就不比再次计算了
定义二维数组memo,一旦其中的值大于1,那显然是计算过了,不比再算。
之后memo再次加上沿着上下左右四个方向最长路径的最大值,就是本点出发,组成最大上升路径的结果
网格类问题BFS
面试题13. 机器人的运动范围
https://leetcode-cn.com/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof/
https://leetcode-cn.com/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof/solution/ji-qi-ren-de-yun-dong-fan-wei-by-leetcode-solution/
模板参考:https://leetcode-cn.com/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof/solution/bfsmo-ban-yi-ci-bei-hui-chu-chu-shi-yong-by-fuxuem/
本题使用BFS更好理解,更好计算,下面我没看这类问题的模板:
int movingCount(int m, int n, int k) {
if(!k) return 1;
queue> Q;//设置队列
vector> used(m, vector(n, 0));
//根据题意,看看是否需要记录已经访问的地方
Q.push(make_pair(0, 0));//插入初始点
int dx[n] = {.....};
int dy[n] = {.....};//方便后续循环赋值
while(!Q.empty())
{
auto [x,y] = Q.front();//auto front = Q.front();
Q.pop();
for(能够达到的点)
{
int tx = dx[i]+x;//int tx = dx[i]+front.first;
int ty = dy[i]+y;//int ty = dy[i]+front.second;
if (不符合要求(越界等情况)) continue;
Q.push(make_pair(tx, ty));//该点可访问,进行记录
used[tx][ty] = 1;//该点被访问,要记录
}
}
return ans;
} 和二叉树的BFS非常相似。
那么对于本题,由于形势特殊,采用如下的方式进行搜寻
下面我们来看完整版本的代码:
class Solution {
public:
int movingCount(int m, int n, int k) {
if(!k) return 1;//k = 0的情况
queue> Q;
vector > used(m, vector(n, 0));//记录已经访问的地方,不要
Q.push(make_pair(0, 0));//插入初始点
used[0][0] = 1;
int ans = 1;
// 向右和向下的方向数组
int dx[2] = {0, 1};
int dy[2] = {1, 0};
while(!Q.empty())
{
auto front = Q.front();
Q.pop();
for(int i = 0;i<2;++i)
{
int tx = dx[i]+front.first;
int ty = dy[i]+front.second;
if (tx < 0 || tx >= m || ty < 0 || ty >= n || used[tx][ty] || isValid(tx) + isValid(ty) > k) continue;
Q.push(make_pair(tx, ty));
used[tx][ty] = 1;
ans++;
}
}
return ans;
}
int isValid(int x) {
int res=0;
while (x) {
res += x % 10;//取余
x /= 10;//移位
}
return res;
}
};
综合题目
130. 被围绕的区域
思路参考:
https://leetcode-cn.com/problems/surrounded-regions/solution/bfsdi-gui-dfsfei-di-gui-dfsbing-cha-ji-by-ac_pipe/
本题不好下手,因为与边界连接的0,全部不能处理,那么我们就按照这个要求,首先对和边界0相互接壤的0进行处理
让其变成其他符合(比如A),然后再深度或者广度遍历,把没有变成A的0,全部变成X。
示意图如图所示:
图源:https://leetcode-cn.com/problems/surrounded-regions/solution/dfs-bfs-bing-cha-ji-by-powcai/
那么我们首先使用BFS将边界上的0和与边界0联通的0全部处理
然后DFS遍历,寻找目前还有没有不是A的0
class Solution {
public:
void solve(vector>& board) {
if(board.empty()) return;
int row = board.size(),col = board[0].size();
//边界0处理
for(int i = 0;i>& board,char before,char After)
{
queue> Q;
int row = board.size(),col = board[0].size();
vector> Used(row,vector(col,false));
Q.push(make_pair(0,0));//从0开始
if(board[0][0] == before) board[0][0] = After;//对初始内容也要判断
int dx[2]={0,1};
int dy[2]={1,0};
Used[0][0] = true;
while(!Q.empty())
{
auto front = Q.front();
Q.pop();
for(int i = 0;i<2;++i)
{
int r = front.first+dx[i];
int c = front.second+dy[i];
if(r>=0&&r=0&&c>& board,int r,int c)
{
int row = board.size(),col = board[0].size();
if(r<0||r>=row||c<0||c>=col||board[r][c]!='O') return;
board[r][c] = 'A';
dfs(board,r+1,c);
dfs(board,r-1,c);
dfs(board,r,c+1);
dfs(board,r,c-1);
}
}; 827. 最大人工岛
https://leetcode-cn.com/problems/making-a-large-island/
一个一个改一个一个试,显然是有问题的,但是我们不妨试试这种暴力解法:
class Solution {
public:
int largestIsland(vector>& grid) {
//对于每个0,先变成1,计算联通面积
if(grid.empty()) return 0;
int row = grid.size(),col = grid[0].size();
int MAX = 0;
for(int i = 0;i>& grid)
{
int row = grid.size(),col = grid[0].size();
if(brow<0||brow>row-1||bcol<0||bcol>col-1) return 0;
int num = 0;
queue>Q;//BFS必备队列,压入坐标
vector> Used(row,vector(col,0));//记录坐标是否被访问
Q.push(make_pair(brow,bcol));
while(Q.size())
{
int size = Q.size();
for(int i = 0;iTemp = Q.front();Q.pop();
int nr = Temp.first,nc = Temp.second;
if(Used[nr][nc] != 1) num++;//此处务必要进行判断,否则会重复计算一些点
Used[nr][nc] = 1;
if(nr+1<=row-1&&Used[nr+1][nc] != 1&&grid[nr+1][nc] == 1)
Q.push(make_pair(nr+1,nc));
if(nr-1>=0&&Used[nr-1][nc] != 1&&grid[nr-1][nc] == 1)
Q.push(make_pair(nr-1,nc));
if(nc+1<=col-1&&Used[nr][nc+1] != 1&&grid[nr][nc+1] == 1)
Q.push(make_pair(nr,nc+1));
if(nc-1>=0&&Used[nr][nc-1] != 1&&grid[nr][nc-1] == 1)
Q.push(make_pair(nr,nc-1));
}
}
return num;
}
};
具体解法参考:https://leetcode-cn.com/problems/making-a-large-island/solution/zui-da-ren-gong-dao-by-leetcode/
有向无环图
介绍内容参考:
https://leetcode-cn.com/problems/course-schedule/solution/bao-mu-shi-ti-jie-shou-ba-shou-da-tong-tuo-bu-pai-/
现在假设,我们在完成事件B之前,必须完成事件A;这就构成了一组先决条件:【B,A】
那么我们现在假设有以下n件事件需要完成,有先决条件如下:
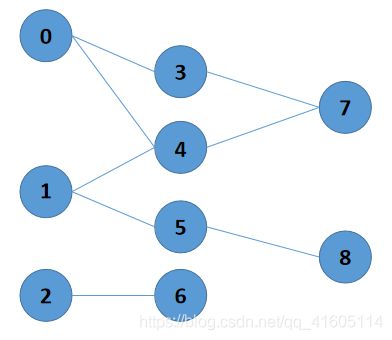
【3,0】,【4,0】,【1,4】,【1,5】,【2,6】,【3,7】,【4,7】,【5,7】
那么构成了上面一个有向无环图,而这对这样一个图进行遍历,就叫做拓扑排序
有向图 中有 入度 和 出度 概念:如果存在0—>1,那么1的入度就是1,0的出度是1;
那么我们现在考虑如何遍历这个图,我们需要完成所有的前序任务,才能继续进行
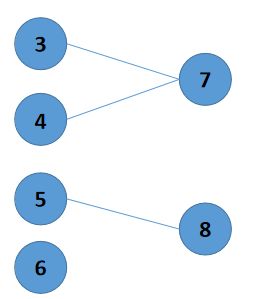
也就是说,我们比如先遍历入度为0的点,之后,将这些点标记为已经遍历,比如现在我们遍历0,1,2这三个点:
那么完成之后,3,4,5,6变成了入度为0的点,我们继续遍历,之后只剩下7,8,两个点,对这两个进行遍历之后,整个遍历完成。
那么代码怎么实现呢?
我们需要一个数组,实时记录每个点的入度情况,即:
入度情况记录:
vector indegree(numCourses,0);//初始阶段假设入度都是0
//入度数组,关心每门课的入度,索引是课的名称,value是课的入度 然后我们需要一记录课程之间关系的数组
关系记录:
vector> graph(numCourses);
//信赖关系,索引是课程名称,value是后续课程 我们用一个数组进行记录,索引的任务名称,值是后续任务,但是一个任务的后续任务有很多,那么我们就需要把数组变成二维数组
我们对这个二维数组进行初始化:
vector v;
for(int i = 0;i 其中的size是任务的个数,我们创建和任务等长的索引,至于第二维,那么就要根据后续任务的个数来确定了
之后我们对上面提到的两个数组初始化:
for(int i = 0;i下面我们就可以进行遍历了:
int cnt = 0;
while (myqueue.size())
//选择入度为0的课程后,查看这些课程的后续,如果入度为0,那么压入队列,直到遇到环为止
{
int temp = myqueue.front();
myqueue.pop();
cnt++;//记录个数
for (int i = 0; i < graph[temp].size(); i++)//temp的后续全部看一遍
{
indegree[graph[temp][i]]--;//入度情况实施把控
if (indegree[graph[temp][i]] == 0)//一旦入度为0,那么就可以进行访问了
myqueue.push(graph[temp][i]);
}
}
下面我们来看相关有向无环图的相关题目:
207. 课程表
https://leetcode-cn.com/problems/course-schedule/
拓扑排序(BFS在(有向)图中的特有名称)
算法参考:https://leetcode-cn.com/problems/course-schedule/solution/tuo-bu-pai-xu-by-liweiwei1419/
liweiwei1419大佬在上述链接中对BFS进行了详细的讲解
我们可以单纯的从题意理解到,如果课程之间彼此互为先修课程,那么我们无法完成学习。因为课程之间形成了一个环
我们遍历图,看看有没有环即可
class Solution {
public:
bool canFinish(int numCourses, vector>& prerequisites) {
vector indegree(numCourses,0);//初始阶段假设入度都是0
//入度数组,关心每门课的入度,索引是课的名称,value是课的入度
vector> graph(numCourses);
//信赖关系,索引是课程名称,value是后续课程
vector v;
for(int i = 0;i myqueue;
for(int i = 0;i 代码参考:https://leetcode-cn.com/problems/course-schedule/solution/c-jian-ji-yi-dong-de-ke-cheng-biao-tuo-bu-pai-xu-b/
210. 课程表 II
https://leetcode-cn.com/problems/course-schedule-ii/
比起上一题,本题更加贴近BFS的遍历
class Solution {
public:
vector findOrder(int numCourses, vector>& prerequisites) {
vector indegree(numCourses,0);//入度
vector>graph(numCourses);//关系
vectorTemp;
for(int i = 0;iRes;//保存结果
queueQ;
for(int i = 0;i{};//不能有环
}
};
下面这道题看似是一道拓扑排序,但是不是
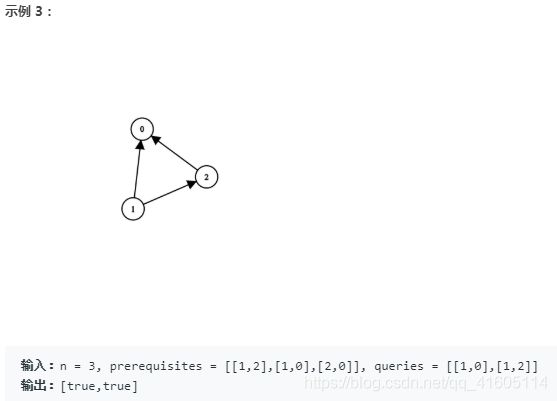
1462. 课程安排 IV
https://leetcode-cn.com/problems/course-schedule-iv/
本题更适合floyd算法,算法介绍:https://blog.csdn.net/Puppet__/article/details/76146848
class Solution {
public:
vector checkIfPrerequisite(int n, vector>& prerequisites, vector>& queries) {
vector> d(n, vector(n,false));
//从i出发,到达j,能否走通
//base case
for(auto p: prerequisites)
d[p[0]][p[1]] = true;
// floyd模板
for(int k = 0; k < n; k++)
for(int i = 0 ; i < n; i++)
for(int j = 0; j < n; j++)
if(d[i][k] && d[k][j])
d[i][j] = true;
vector res;
for(auto q : queries)
res.push_back(d[q[0]][q[1]]);
return res;
}
};
代码参考:https://leetcode-cn.com/problems/course-schedule-iv/solution/c-zhong-gui-zhong-ju-de-500msjie-fa-you-xiang-tu-d/
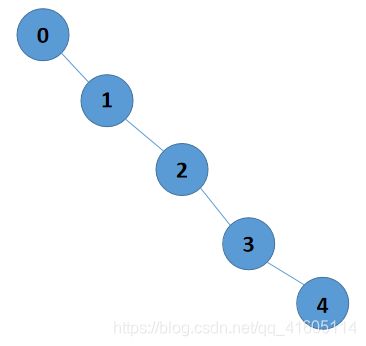
我们的目的是将路径串联起来,举个例子
我们假设dp如下:
那么按照题意,dp【0】【4】也是true,所以我们现在要将他们连接起来:
比如0和2,1是中介,如果dp[0][1]存在,dp[1][2]也存在,那么说明dp[1][2]也存在,所以有了:
for(int k = 0; k < n; k++)
for(int i = 0 ; i < n; i++)
for(int j = 0; j < n; j++)
if(d[i][k] && d[k][j])
d[i][j] = true;k就是中介,i和j分别是开头和结尾
算法参考:https://leetcode-cn.com/problems/course-schedule-iv/solution/floydde-sao-cao-zuo-chuan-di-bi-bao-by-yang-198/
广度优先遍历
寻找无向无权图中最短路径:
内容参考:https://leetcode-cn.com/problems/word-ladder/solution/yan-du-you-xian-bian-li-shuang-xiang-yan-du-you-2/
127. 单词接龙
https://leetcode-cn.com/problems/word-ladder/
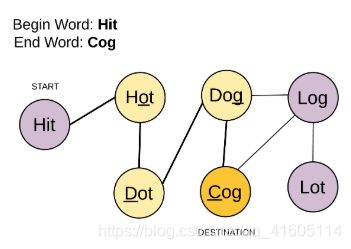
题意可以总结如下:
图源:https://leetcode-cn.com/problems/word-ladder/solution/dan-ci-jie-long-by-leetcode/
可以把问题抽象为无向无权图,使用BFS找到最短路径
解法参考:https://leetcode-cn.com/problems/word-ladder/solution/bfszi-dian-shu-by-elvis-10/
126. 单词接龙 II https://leetcode-cn.com/problems/word-ladder-ii/