这个月内的一些有趣的题
Letter Array
http://codeforces.com/gym/100482/problem/C
tag: 线段树加懒人标记O(mlogn)或前缀和 O(Σ(r-l+1))
题解:
- 因为排序只影响区间[l,r]的前缀和,其他不影响,所以只更改[l,r]的前缀和就可以了。
- 但我一看到区间修改就想到线段树加懒人标记了,所以自己就实现了个。
- 需要注意的是排序操作,可能把一个结点对应区间的元素值移动到与它毫不相关的区间结点上,所以需要先查询一次统计元素值,再找到对应区间挨个倒出来。
#include
#include
using namespace std;
const int MAXN = 1e5+1e3;
#define dbg 1
struct Seg{
int cnt[27], sz;
bool srt;
Seg() {
clr();
srt = false;
sz = 0;
}
void clr() {
memset(cnt, 0, sizeof(cnt));
}
Seg operator + (const Seg& b) {
Seg c;
for(int i=0; i<26; ++i) {
c.cnt[i] = cnt[i]+b.cnt[i];
c.sz += c.cnt[i];
}
return c;
}
}seg[MAXN<<2], ans;
char s[MAXN];
int len, l, r;
void build(int id, int tl, int tr) {
seg[id].sz = tr-tl+1;
seg[id].clr();
if(tl==tr) {
++seg[id].cnt[s[tl]-'A'];
return;
}
int tm=tl+tr>>1;
build(id<<1, tl, tm);
build(id<<1|1, tm+1, tr);
seg[id] = seg[id<<1]+seg[id<<1|1];
}
void pushdown(int id) {
int lch=id<<1;
int rch=id<<1|1;
int lsz = seg[lch].sz;
int rsz = seg[rch].sz;
seg[lch].clr();
seg[rch].clr();
seg[lch].srt=seg[rch].srt=true;
for(int i=0; i<26&&lsz; ++i) {
if(lsz>=seg[id].cnt[i])
lsz -= (seg[lch].cnt[i]=seg[id].cnt[i]);
else {
seg[lch].cnt[i]=lsz;
lsz=0;
}
}
for(int i=25; i>-1&&rsz; --i) {
if(rsz>=seg[id].cnt[i])
rsz -= (seg[rch].cnt[i]=seg[id].cnt[i]);
else {
seg[rch].cnt[i]=rsz;
rsz=0;
}
}
}
void Sort(int id, int tl, int tr) {
if(l<=tl&&tr<=r) {
int sz = seg[id].sz;
seg[id].clr();
for(int i=0; i<26&&sz; ++i) {
if(sz>=ans.cnt[i]) {
sz -= (seg[id].cnt[i]=ans.cnt[i]);
ans.cnt[i] = 0;
}
else {
ans.cnt[i] -= (seg[id].cnt[i] = sz);
sz = 0;
}
}
seg[id].srt = true;
return;
}
if(tl>1;
if(tl<=r&&tm>=l) Sort(id<<1, tl, tm);
if(tm=l) Sort(id<<1|1, tm+1, tr);
seg[id] = seg[id<<1]+seg[id<<1|1];
}
void query(int id, int tl, int tr) {
if(l<=tl&&tr<=r) {
ans = ans+seg[id];
return;
}
if(tl>1;
if(tl<=r&&tm>=l) query(id<<1, tl, tm);
if(tm=l) query(id<<1|1, tm+1, tr);
}
int main() {
int t, kcase=0;
scanf("%d", &t);
while(t--) {
scanf("%s", s);
len = strlen(s);
build(1,0,len-1);
int m;scanf("%d", &m);
printf("Case #%d:\n", ++kcase);
while(m--) {
char cmd[3];
scanf("%s%d%d", cmd, &l, &r);
ans.clr();
if(cmd[0]=='g') {
query(1, 0, len-1);
for(int i=0; i<26; ++i)
{
if(i) putchar(' ');
printf("%d", ans.cnt[i]);
}
puts("");
}
else {
query(1, 0, len-1);
Sort(1, 0, len-1);
}
}
}
return 0;
}
Training Camp
https://vjudge.net/problem/Gym-100676G
tag: dp
题解:
- 印象非常深刻,个人想着用拓扑排序加贪心的办法,找到当前可以选的值最小的点,把他删去,依次下去.但提交后一直WA, 补题时也是如此,搞得都想日站了。
- 后来想到一点,自己的解法不一定是最优的,比如数据
1
3 1
a 1
b 3
c 4
c -> a
最佳排列为 c, a, b 而非 b, c, a.
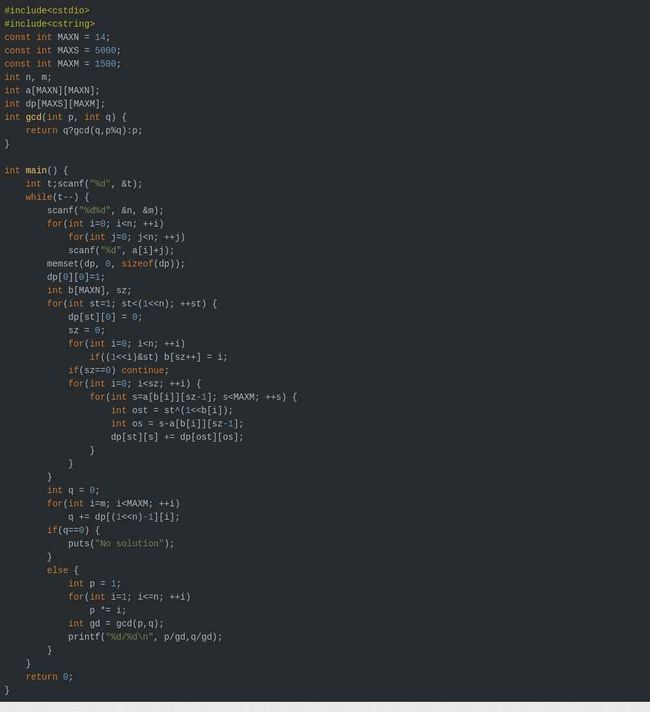
Problem Arrangement
https://vjudge.net/problem/ZOJ-3777
tag: dp
题解:
1.这回长记性了,遇到求排列权值的首先想的是dp;
2.要求权值>=m的方法数,用的是一个很经典的套路。
Paint the Grid Again
https://vjudge.net/problem/ZOJ-3780
tag: 拓扑排序
题解:一道拓扑排序的建模,但不知道为什么我的逆推法不行。