F1 micro macro 区别和详解

micro-F1和macro-F1详解

• • 摘要
  • micro-F1：
  • macro-F1：
  • weighted-F1
  • 调参

 

摘要

F1-score：是统计学中用来衡量二分类模型精确度的一种指标，用于测量不均衡数据的精度。它同时兼顾了分类模型的精确率和召回率。F1-score可以看作是模型精确率和召回率的一种加权平均，它的最大值是1，最小值是0。

在多分类问题中，如果要计算模型的F1-score，则有两种计算方式，分别为micro-F1和macro-F1，这两种计算方式在二分类中与F1-score的计算方式一样，所以在二分类问题中，计算micro-F1=macro-F1=F1-score，micro-F1和macro-F1都是多分类F1-score的两种计算方式；

假设有如下的三分类结果：

根据上述结果我们可以得到一下结果（多分类中每一类都有Precision、Recall和F1-score）：

两种多分类F1-score的计算方法：

micro-F1：

取值范围：(0, 1)；
适用环境：多分类不平衡，若数据极度不平衡会影响结果；
计算方式：

TPi 是指第 i 类的 True Positive 正类判定为正类;
FPi 是指第 i 类的 False Positive 负类判定为正类;
TNi 是指第 i 类的 True Negative 正类判定为负类;
FNi 是指第 i 类的 False Negative 负类判定为负类。

假设现在有一下的三分类结果：

由此表我们可以得出：
对第1类：FP1=d+g；TP1=a；FN1=b+c；TN1=e+f+h+i；
对第2类：FP2=b+h；TP2=e；FN2=d+f； TN2=a+c+g+i；
对第3类：FP3=c+f； TP3=i； FN3=g+h；TN3=a+b+d+e；

对micro-F1来说，mirco的计算方式使将recall和precision合起来算，所以：

对于micro-Recall：召回率为(TP1+TP2+TP3)/(TP1+TP2+TP3+FN1+FN2+FN3 )，即三个类别的TP和FN相加为分母，TP为分子。由上式分析可知，TP1+TP2+TP3 =a+e+i；FN1+FN2+FN3 =b+c+d+f+g+h（即除了TP之外的所有格），所以得到
对于micro-Precision：精确度为(TP1+TP2+TP3)/(TP1+TP2+TP3+FP1+FP2+FP3 )，同理可得，TP1+TP2+TP3 =a+e+i；FP1+FP2+FP3 =d+g+b+h+c+f（即除了TP之外的所有格），得到

然后，根据micro F1-score的计算方式可得：

而且，对于模型准确性Accuracy，定义为正确分类的样本在所有样本中的比例。所以准确性的公式
Acc=(a+e+i)/(a+b+c+d+e+f+g+h+i)
即：

据此我们可以得出结论：若micro-F1=0.5，则模型准确率Acc=0.5，Precision和Recall均为0.5，但是我们不能得出模型基本是靠猜的结论，因为若是三分类结果如下：
Acc=(a+e+i)/(a+b+c+d+e+f+g+h+i)=micro-F1=Precision_mi=Recall_mi=0.5

macro-F1：

取值范围：(0, 1)；
适用环境：多分类问题，不受数据不平衡影响，容易受到识别性高（高recall、高precision）的类别影响；
计算方法：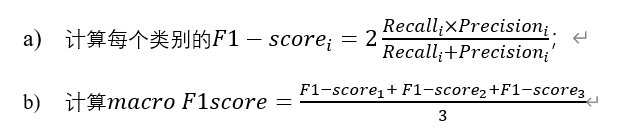

macro-F1有两种计算方式，

1、先求macro-Recall和macro-Pecision，之后由这两个和求macro-F1；
2、对三个类别的F1-score直接求平均。

在sklearn的包中，使用的是第二种方式，两种方式的使用争议一直存在，但在“Training algorithms for linear text classifiers（ Lewis, David D., et al. “Training algorithms for linear text classifiers.” SIGIR. Vol. 96. 1996.）”中，作者指出，macro-F1是所有类中F1-score的平均值，即第二种方式才是macro-F1的计算方式。

我们对两种求平均的方法也可以分析，第一种方式对错误的分布不太敏感“详见论文（Opitz, Juri, and Sebastian Burst. “Macro F1 and Macro F1.” arXiv preprint arXiv:1911.03347 (2019)）”，这一点有点像micro-F1；而第二种方法则被上述论文作者推荐。

同样，我们对每一类的指标都进行分析：
对第1类：FP1=d+g；TP1=a；FN1=b+c；TN1=e+f+h+i；
对第2类：FP2=b+h；TP2=e；FN2=d+f； TN2=a+c+g+i；
对第3类：FP3=c+f； TP3=i； FN3=g+h；TN3=a+b+d+e；

将上述的值带入macro-F1中，得到：

上式即为macro-F1的公式（算到这里我就没有继续化简了感觉没东西）

若使该值=0.5，也得不到有用的结论。

weighted-F1

除了micro-F1和macro-F1，还有weighted-F1，是一个将F1-score乘以该类的比例之后相加的结果，也可以看做是macro-F1的变体吧。例如：

对上述表格，我们可得出precision、recall和F1-score：

所以，对weighted-F1：

同样，我们也可以算weighted-Precision和weighted-Recall：

其实从上面我们也可以看出来，weighted-F1并不等于由weighted-Precision和weighted-Recall计算得出的Weighted-F1(这里为了分别用大写表示)，同理，参考macro的两种计算方式。一般以第一种为结果。

weighted-F1和macro-F1的区别在于：macro-F1对每一类都赋予了相同的权重，而weighted-F1则根据每一类的比例分别赋予不同的权重。

调参

关于scoring的使用：

进行网格调参时，构建GridSearchCV，一般二分类的评分标准为roc_auc，而多分类并不提供roc曲线面积的评分方式，所以在多分类时，我们可以用

grid_search = GridSearchCV(lg, n_jobs=-1, scoring='f1_weighted', param_grid=param_dist, cv=10, verbose=5)

• 1

等评分方式来进行调参，不同的评分方式对结果都会有影响。
还有更多的评分方式可以运行这两行代码获得：

import sklearn.metrics as sm
print(sorted(sm.SCORERS.keys()))

 

 

补充

'micro':Calculate metrics globally by counting the total true positives, false negatives and false positives.

'micro':通过先计算总体的TP，FN和FP的数量，再计算F1

'macro':Calculate metrics for each label, and find their unweighted mean. This does not take label imbalance into account.

'macro':分布计算每个类别的F1，然后做平均（各类别F1的权重相同）

 

“微”（micro）平均：计算所有类别中假正例、假反例和真正例的总数，然后利用这些计数来计算准确率、召回率和f1 分数。

“宏”（macro）平均：计算未加权的按类别f1 分数。它对所有类别给出相同的权重，无论类别中的样本量大小。

如果对每个样本等同看待，那么推荐使用“微”平均f1 分数；如果对每个类别等同看待，那么推荐使用“宏”平均f1 分数

 

F-beta score

当beta大于1，更多关注recall；当beta小于1，更多关注precision

除了F1分数之外，F0.5分数和F2分数，在统计学中也得到了大量应用，其中，F2分数中，召回率的权重高于精确率，而F0.5分数中，精确率的权重高于召回率