说明：
- 文章所有内容截选自实验楼教程【3个C语言实例带你掌握递归方法论】，教程里还有两个实例，感兴趣的可以点击查看；
- 文章主要是带你通过解决这个游戏来利用递归解决实际问题并掌握其核心思想，懂得如何使用递归解决实际问题；
“汉诺塔”游戏规则
首先，我们来看一下“汉诺塔”游戏规则：
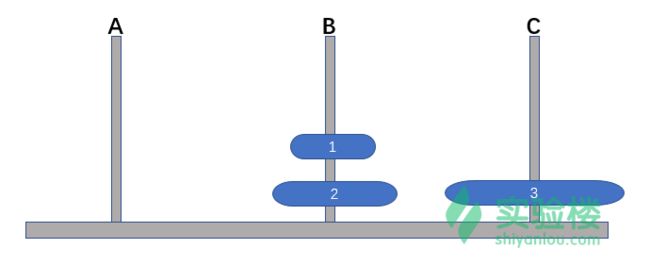
有三根杆子A，B，C。A杆上有N个(N>1)穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C杆：
- 每次只能移动一个圆盘；
- 大盘不能叠在小盘上面。
假设有三个盘，游戏的过程如下图(图片来源于维基百科)：
好了，给你1分钟，你可以思考你如何解决这个问题！
思考后，我们会发现汉诺塔问题，使用传统的思维方式去寻求解决方案，并不是那么容易，当然不排除很擅长这类游戏的人。
这时候，学程序的各位程序员们，就可以采用递归的方式来解决这个问题啊！·
什么是递归
在解决“汉诺塔”问题之前，我们先来看看在解决过程中会用到的“递归”概念。
我们先来看维基百科上的定义：
递归（英语：Recursion），又译为递回，在数学与计算机科学中，是指在函数的定义中使用函数自身的方法。递归一词还较常用于描述以自相似方法重复事物的过程。
有点抽象啊，那我们先讲个故事吧：
从前有座山，山里有座庙，庙里有个老和尚，正在给小和尚讲故事，故事的内容是：
从前有座山，山里有座庙，庙里有个老和尚，正在给小和尚讲故事，故事的内容是：
从前有座山，山里有座庙，庙里有个老和尚，正在给小和尚讲故事，故事的内容是：
....
很熟悉的一个故事吧，我们再从感观来了解一下什么是递归，看下图(图片来源于互动百科)：
从上面两个例子中，我们了解到，递归的本质就是相似的重复。
在计算机领域中，递归作为一种算法策略常用于解决某类特定问题。哪一类问题适合用递归算法来解决呢？
适合使用递归方法的来解决的问题，具备以下两个特点：
- 该问题可以分解成规模更小但形式相同的子问题来解决
- 该问题分解到最后，可以得到基准情况，该情况下无需递归就能解决问题
在计算机领域，解决递归问题，是通过递归函数实现的。递归函数是一种调用自身的函数，一个递归函数通常具备以下形态：
递归函数(输入)
{
if (是基准情况)
return 基准情况下问题的解
输入 = 规模更小的但形式相同的问题
return 递归函数(输入)
}
使用递归解决“汉诺塔”游戏
在实现的编程中，有些问题按照传统的思维方式去寻求解决方案，会异常困难，但如果我们用递归的方式去解决问题则异常的简单，甚至简单到我们给出程序解决了问题，还有可能搞不明白问题到底是怎么解决的。
当然在使用递归解决问题之前，我们必须要学会用递归的方法去思考问题。
下面我们试图使用C程序来解决一个益智游戏--汉诺塔:
关于“汉诺塔”的游戏规则，一开始已经说得很明白了，这里就不再叙述了。
使用递归解决实际问题，需要找准两个关键点：
- 基准情况，不需使用递归解决，一般能轻易得出答案的情况
- 如何将问题分解为规模更小但形式相同的子问题
对于汉诺塔而言，只有一个盘时，就是基准情况，我们可以直接将盘从源杆移动到目标杆：
// 移动一个盘
// disk为需要移动的盘符，src为源杆，dest为目标杆
void move_single_disk(int disk, char src, char dest)
{
fprintf(stdout, "disk%d: %c --> %c\n", disk,src,dest);
}
下面我们来看一下非基准情况下，汉诺塔解决思路。
我们假设我们的初始问题是：有三个盘1、2、3，三个杆A、B、C，将所有盘从A移到C：
那么我们的解决思路：
-
将盘1和盘2移动到B杆：
此处输入图片的描述 -
将盘3移动到C杆：
此处输入图片的描述 -
将盘1和盘2移动到C杆：
此处输入图片的描述
在这个解决过程中，可以看到我们将汉诺塔问题分解成了规模更小但形式相同的子问题：
-
将盘1和盘2移动到B杆时，我们可以看成是这样一个汉诺塔问题，有两个盘1、2，三个杆A、B、C，需要将所有盘从A杆移动到B杆，我们只需将B杆和C杆的名字换一下就变成了跟我们的初始问题形式一样的但规模跟小的问题了：
此处输入图片的描述 -
将盘3移动到C杆，我们可以看成这样一个汉诺塔问题，只有一个盘3，三个杆A、B、C，需要将盘3从A杆移动到C杆：
此处输入图片的描述 -
将盘1和盘2移动到C杆时，我们可以看成是这样一个汉诺塔问题，有两个盘1、2，三个杆A、B、C，需要将所有盘从B杆移动到C杆，我们只需将A杆和B杆的名字换一下就变成了跟我们的初始问题形式一样的但规模跟小的问题了：
此处输入图片的描述
将上述思路整理成伪代码：
// n个盘，盘符由小到大为1——>N, 从A杆移动到C杆
void hanoi(n个盘，A杆， B杆，C杆)
{
// 解决子问题一
hanoi(n-1个盘，A杆，C杆，B杆)；
// 解决子问题二
hanoi(1个盘，A杆，B杆，C杆)；
// 解决子问题三
hanoi(n-1个盘，B杆，A杆，C杆);
}
加入基准情况，我们的汉诺塔函数实现如下：
// 汉诺塔函数，递归方式
// n个盘，n个盘，盘符由小到大为1——>N, 从A杆移动到C杆
// disk 为最大盘的盘符
void hanoi(int n, int disk, char A, char B, char C)
{
// 基准情况
if (1 == n) {
move_single_disk(disk ,A, C);
} else {
// 解决子问题一
hanoi(n-1, disk-1, A, C, B);
// 解决子问题二
hanoi(1, disk, A, B, C);
// 解决子问题三
hanoi(n-1, disk-1, B, A, C);
}
}
完整代码(hanoi.c)：
/*
* file name : hanoi.c
*/
#include
// 移动一个盘
// disk为需要移动的盘符，src为源杆，dest为目标杆
void move_single_disk(int disk, char src, char dest)
{
static step = 1;
fprintf(stdout, "step%d: disk%d %c --> %c\n", step++,disk,src,dest);
}
// 汉诺塔函数，递归方式
// n个盘，n个盘，盘符由小到大为1——>N, 从A杆移动到C杆
// disk 为最大盘的盘符
void hanoi(int n, int disk, char A, char B, char C)
{
// 基准情况
if (1 == n) {
move_single_disk(disk ,A, C);
} else {
// 解决子问题一
hanoi(n-1, disk-1, A, C, B);
// 解决子问题二
hanoi(1, disk, A, B, C);
// 解决子问题三
hanoi(n-1, disk-1, B, A, C);
}
}
int main(int argc, char *argv[])
{
int n = atoi(argv[1]);
fprintf(stdout, "=======hanoi(%d):\n", n);
hanoi(n, n, 'A', 'B', 'C');
fprintf(stdout, "=======hanoi finished\n");
return 0;
}
演示：
编译命令:
$ gcc -o hanoi hanoi.c
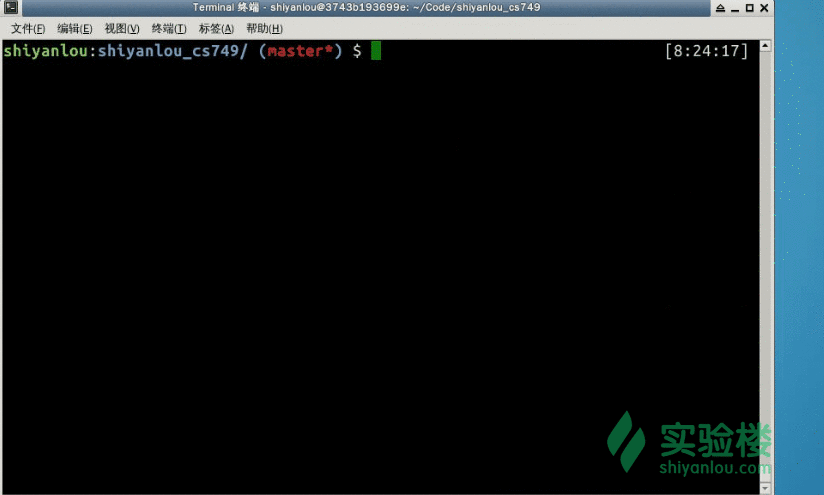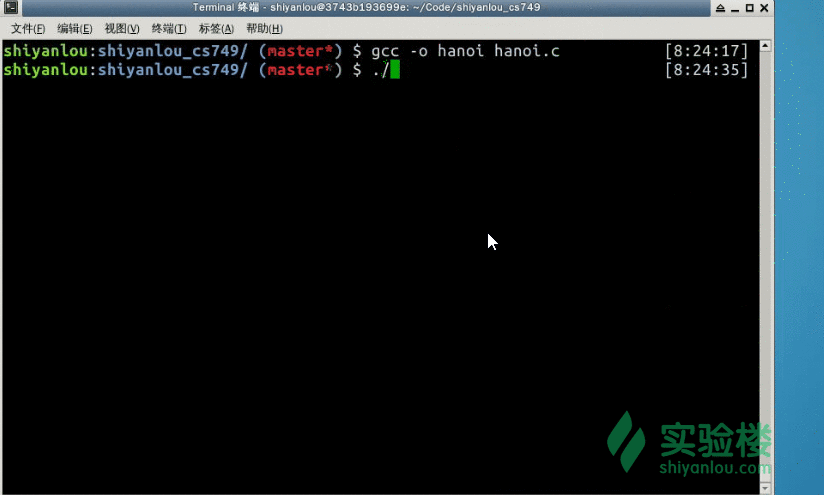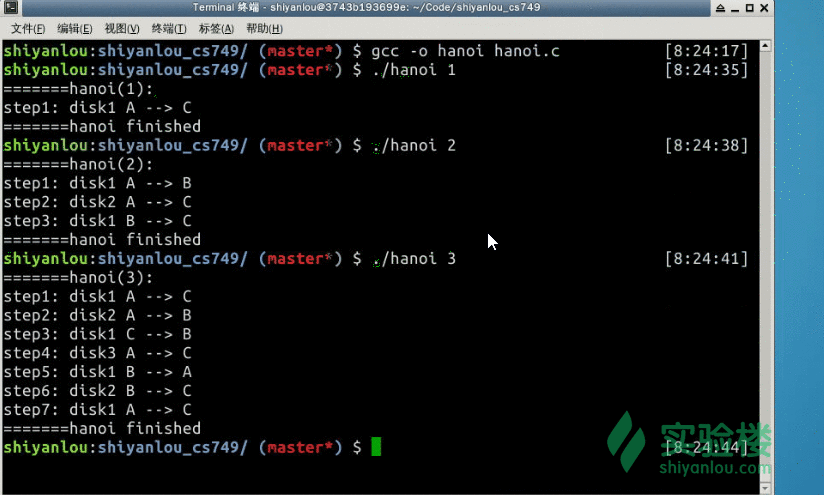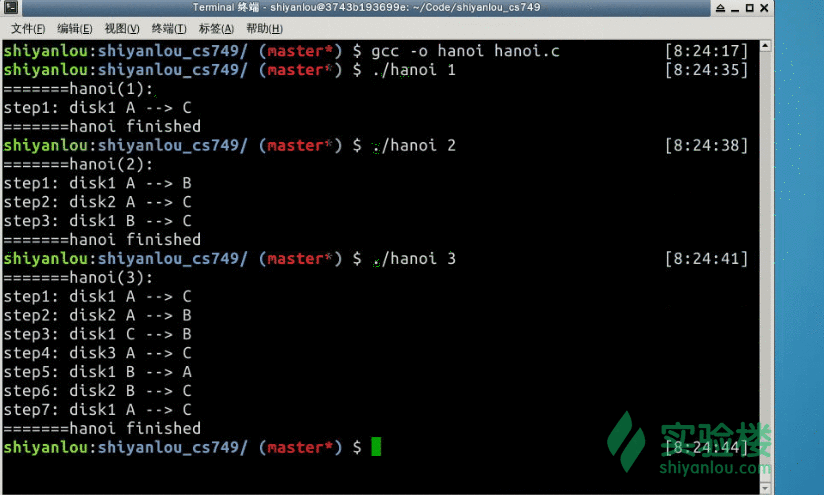
结果：
读者朋友可根据程序给出来的解，自行验证其正确性：
最后：
文章所有内容截选自实验楼教程【3个C语言实例带你掌握递归方法论】，教程里还有两个实例，感兴趣的可以点击查看；
教程里的另外两个实例分别是：
- 使用递归解决数学问题：实现一个递归函数来求斐波那契数列上第N项的值；
- 更加高效解决斐波那契数列：更高效更快的方式来解决斐波那契数列；
感兴趣的点击【3个C语言实例带你掌握递归方法论】即可查看如何用递归来解决哦~