“浪潮杯”第九届山东省ACM大学生程序设计竞赛重现赛 H Dominoes (BFS)
链接:https://www.nowcoder.com/acm/contest/123/H
来源:牛客网
题目描述
Orz likes to play dominoes. Now giving an n∗m chessboard and k dominoes whose size are 1∗2, Orz finds that there is exactly one grid empty, so that he can move dominoes without overlapping them. An initial situation is given, he wants to know how many final situation could be achieved, except the initial situation. Note every domino is different, as they have their own serial number. Since the answer may be very large, please output the answer modulo 1000000009.
输入描述:
There will be multiple test cases. For each test
case:
The first line contains three integers: n,m,k(n≤9,m≤10000).
The following k lines, each line contains four
integers: a b c d, indicating that this domino occupies (a, b) and (c, d).
The input guarantees that the domino does not
overlap, and there is exactly one empty grid.输出描述:
For each test cases, output the answer modulo
1000000009.
示例1
输入
复制
5 5 12
1 1 2 1
1 2 2 2
1 3 2 3
1 4 1 5
2 4 2 5
3 4 3 5
3 1 3 2
4 1 4 2
5 1 5 2
4 3 5 3
4 4 5 4
4 5 5 5输出
复制
81.题意:
现在给出一个n∗m棋盘和k个多米诺骨牌,其大小为1∗2,且只有一个网格是空的,这样他就可以移动多米诺骨牌而不重叠它们。求有多少最终情况可以实现,除了最初的情况。每个多米诺骨牌都是不同的,因为他们有自己的序列号。输出答案取余1000000009。
2.思路:
按空格位置(右上角顶点)进行搜索,检查状态合不合格就好:
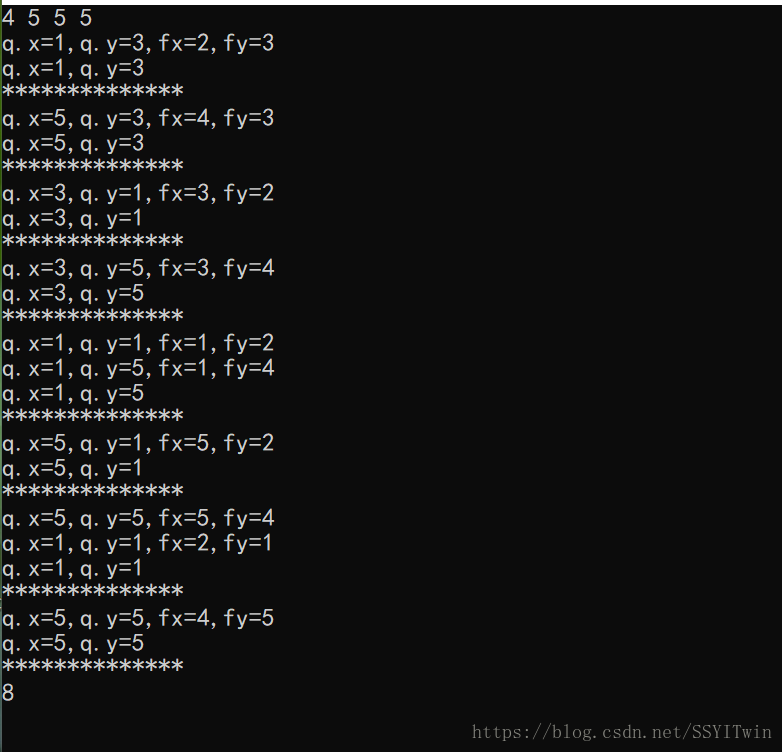
如上图所示的题目样例, 5*5的格子,12张诺骨牌,最开始标记空格的位置是(3,3),然后进行广搜,八个位置如下:
特别注意有一个要判断的就是,属不属于一个多骨诺牌:设空格现在位于(3,3)移动后到达(1,3) 。现在搜索的时候让它往下面移动,就会到达(1,1)这个位置,由上面的图片我们知道,这显然是不合适的,因为(1,1)和(1,2)属于不同的颜色。
3.代码:
#include
using namespace std;
typedef long long LL;
const LL mod = 1e9+7;
int n,m,k;
int mp[10][10010];
int vis[10][10010];
int dir[4][2]={-2,0,2,0,0,-2,0,2};
struct node
{
int x,y;
};
int judge( int x , int y )
{
if ( x<1||x>n||y<1||y>m )
return 0;
else
return 1;
}
int bfs( int sx , int sy )
{
memset (vis,0,sizeof(vis));
node p,q;
p.x = sx;
p.y = sy;
queueQ;
Q.push(p);
vis[p.x][p.y] = 1;
while ( !Q.empty() )
{
//int dir[4][2]={-2,0,2,0,0,-2,0,2};
// 左 右 下 上
p = Q.front();
Q.pop();
for ( int i=0 ; i<4 ; i++ )
{
q.x = p.x + dir[i][0];
q.y = p.y + dir[i][1];
if ( !judge(q.x,q.y)||vis[q.x][q.y] )//越出边界就继续
continue;
int fx=p.x+dir[i][0]/2;
int fy=p.y+dir[i][1]/2;
//cout<<"q.x="<