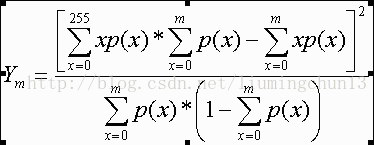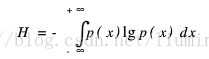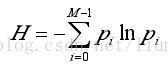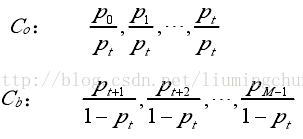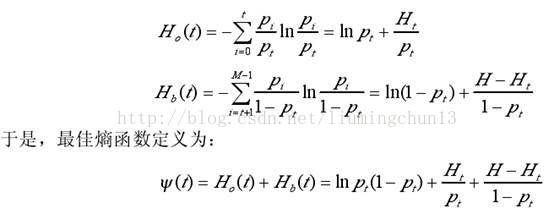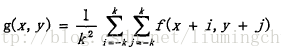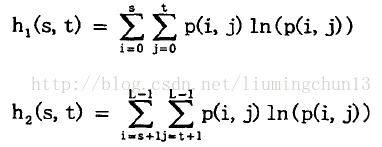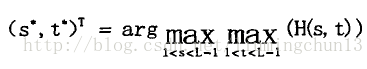图像分割笔记
迭代阈值分割:
迭代法是基于逼近的思想,其步骤如下:
法一:
1. 求出图象的最大灰度值和最小灰度值,分别记为ZMAX和ZMIN,令初始阈值T0=(ZMAX+ZMIN)/2;
2. 根据阈值TK将图象分割为前景和背景,分别求出两者的平均灰度值ZO和ZB
3. 求出新阈值TK+1=(ZO+ZB)/2;
4. 若TK==TK+1,则所得即为阈值;否则转2,迭代计算。
法二:
1. 统计图像灰度直方图
2. 找到最大灰度值ZMAX和最小灰度值ZMIN,并计算T0=(ZMAX+ZMIN)/2
3. 计算小于T0的所有灰度的均值ZO和大于T0的所有灰度的均值ZB(用直方图求就可以)。
例如,你的直方图从10到250有值,则T0 = 260/2 = 130.
ZO = Sum(nHist[i] * i) / Sum(nHist[i]); 10 <= i <= 130
BO = Sum(nHist[i] * i) / Sum(nHist[i]); 131 <= i <= 250
自适应阈值分割
当照明不均匀,有突发噪声或者背景灰度变化较大时,整幅图像分割时将没有合适的单一阈值。因此对于自适应阈值分割的思想,即图像中的每个像素对应的阈值可能不相同。
常用的自适应阈值选取方法是:每个像素的阈值由自身为中心的邻域窗口确定,把中值 均值 或者高斯卷积作为阈值。
上下阈值法:利用正态分布求可信区间
大津法 (OTSU,最大类间方差法):
最大类间方差法是由日本学者大津于1979年提出的,是一种自适应的阈值确定的方法,又叫大津法,简称OTSU。它是按图像的灰度特性,将图像分成背景和目标2部分。背景和目标之间的类间方差越大,说明构成图像的2部分的差别越大,当部分目标错分为背景或部分背景错分为目标都会导致2部分差别变小。因此,使类间方差最大的分割意味着错分概率最小。
对于图像I(x,y),前景(即目标)和背景的分割阈值记作T,属于前景的像素点数占整幅图像的比例记为ω0,其平均灰度μ0;背景像素点数占整幅图像的比例为ω1,其平均灰度为μ1。图像的总平均灰度记为μ,类间方差记为g。
假设图像的背景较暗,并且图像的大小为M×N,图像中像素的灰度值小于阈值T的像素个数记作N0,像素灰度大于阈值T的像素个数记作N1,则有:
ω0=N0/ M×N (1) ω0前景比例
ω1=N1/ M×N (2) ω1背景比例
N0+N1=M×N (3) N0(N1)前景(背景)像素点数
ω0+ω1=1 (4)
μ=ω0*μ0+ω1*μ1 (5) (μ0前景;μ1背景;μ总)平均灰度
g=ω0(μ0-μ)^2+ω1(μ1-μ)^2 (6)
将式(5)代入式(6),得到等价公式:
g=ω0ω1(μ0-μ1)^2 (7)
采用遍历的方法得到使类间方差最大的阈值T,即为所求。
另一种描述方法:灰度级x的点的概率为P(x);则OSTU就是求下式达到最大值的灰度级m。
OSTU多阈值分割
双阈值ostu图像分割代码: http://download.csdn.net/detail/liumingchun13/9863154
最大熵阈值法(几种图像分割阈值选取方法的比较与研究):
一维最大熵阈值法(基于最大熵的灰度阈值选取方法):
1985年Kapur等人提出了一维最大熵阈值法。熵是平均信息量的表征,根据信息论,熵定义为:
其中p(x)是随机变量x的概率密度函数。对于数字图像,x可以是灰度、区域灰度、梯度等特征。根据最大熵原理,用灰度的一维熵求取阈值就是选取一个阈值t使图像分割出来的两部分的一阶灰度统计的信息量最大,即一维熵最大。
假设图像灰度级为[0~M-1],pi为灰度值为i的像素点的概率,设图像灰度阈值为t,t将图像分成目标和背景两类:Co={0,1,2,…,t},Cb={t+1,t+2,…,M-1};则熵可表示为:
假设图像的灰度概率分布为p0,p1,p2,…,pM-1,则由t分成两类后的概率分布为:
即pi表示灰度值为i像素在所在类占的比例,则Co和Cb两类基于概率分布的熵分别为
二维最大熵阈值法:
二维最大熵阈值法中二维指像素灰度值为i同时领域平均灰度值为j的像素点个数n(i, j)。领域平均灰度值定义为:
其中k为搜索领域窗口的尺寸,一般为3.
则二元组(i,j)的概率为P(i,j)=n(i,j)/M*N。
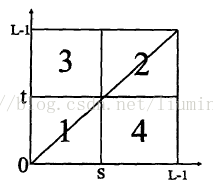
假设((s,t)为图像的分割阈值,0 因此可根据一维信息熵定义离散二维信息熵: 则区域A的信息熵为: 同理B的熵为: 其中 因此最大阈值向量为