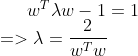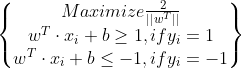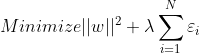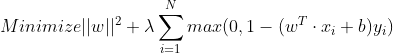NLP学习笔记29-SVM 支持向量机

一 序

   本文属于贪心NLP训练营学习笔记。上一节梯度下降法的收敛推导，整理了半天，真头大。

Linear classifier 回顾

有数据集D={(x1​,y1​),(x2​,y2​),...,(xn​,yn​)},y∈{−1,1},i=1,2,...,n

对于线性模型的参数

决策边界：

判断条件表达式:时，

时，

上面的可以写成:

二 SVM

Max margin

  

假如我们有这样一些数据，有3条线（决策边界）也能完全分开，这里三个分类边界，到底那一条线最好呢？

明显2号要最好，因为它的安全区域最大，对于类似绿色圆圈的噪音扰动perturbation，2号线的robust鲁棒性最好。这个现象也叫：robust to the perturbation。

SVM就是这么样一个方法,接下来看margin的数学表示。

Margin的表示

说明：

1分界线的方程我们知道是，三条线分别设置为：

为啥这里单位取得的是1 而不是10，100，跟单位向量一个原理，我们把看做是  平移的结果。

2 向量w的方向与分界线为什么是垂直的？

假设分界线上有两个点：，那么我们可以写出这两个点满足

两式相减得：,  这个表示w与垂直.

注意，这是空间向量表示的方法。为啥乘积=0就垂直，可看这篇https://blog.csdn.net/u014756380/article/details/77901834

3、Margin的表示

假设是w上两个点，且分别与两个margin边界相交。因此根据这些条件有：

  (式子1)

 (式子2)

 (式子3)

先求，把式子3 代入到式子1，

 

=》  (代入式子2)

=

=  ( 代入)  

SVM的目的就是使得margin值最大。

SVM Objective:Hard Constraint

SVM目标函数，下面是限制条件

按惯例求最大值需要转换为求最小值：

硬约束 是说margin内部是不允许有样本点的（截图的红圈部分），所有点都要在安全区域外。

Soft Constraint（弱限制条件）

硬约束不一定是最合适的，下面的例子进行说明。

采用硬约束会有截图上的问题 ：过拟合，因为硬限制 要求必须100%准确导致的。

硬分类转换为软分类，也就是允许有错误的分类在安全区域，甚至在错误的分类线外。

分类条件作了换个方式表达：st 

修改后变成，目标函数不变，约束条件变成 ，其中 代表犯错程度(slack variable，中文：松弛因子）

当然我们希望这个犯错越小越好，因此可以在目标函数中加入一项，进行约束：

其中是一个平衡参数，当的时候，也就是整个目标函数不允许犯错，因为一旦有错误就会被放大。

Hinge Loss

一般像上面那种的带有约束条件的目标函数，我们能不能想之前拉格朗日函数那种处理，就是要想办法把约束条件融入到目标函数中。

我们要最小化

因此就是要使得 尽量小，由约束可知，

也就是说 最小 时 

还有个补充条件 >0, ==> ( 如果就变成了硬约束的条件了，不符合软约束的假设,可见截图)

目标函数可以写成：

  （目标函数）

其中：

   关于x<0 可以理解为硬约束不产生任何损失,x >0 就是有损失。

其中也叫Hinge Loss。老师说Hinge Loss是很重要的概念，很多地方有广泛的应用，不止是SVM。

到此为止，我们讨论的都是用线性方程来分割样本，所以属于线性SVM（linear SVM）.目标函数已经有了，后面再往下就是用梯度下降来求解最优解。

随机梯度下降算法计算目标函数

观察目标函数，

 

对比下之前的逻辑回归， 是L2正则，而  才是真正的损失函数。

根据之前的约束条件，x<0是 max(0，x)为0，就是不产生损失，也就不需要梯度下降法。

梯度下降法，需要有初始化条件及步长迭代。

首先初始化参数：

然后循环所有样本（参见截图）

然后分情况进行讨论：

当 <=0,就是损失函数为0不产生损失，也就不需要梯度下降法。所以只需要前面的正则项参与梯度运算。

 (这里是套用公式)

 >0 ,分别求损失函数对w和b的偏导

现在这种算法只能计算线性可分的数据.也可以计算非线性的数据，就引出了SVM的由primal-form到dual-form

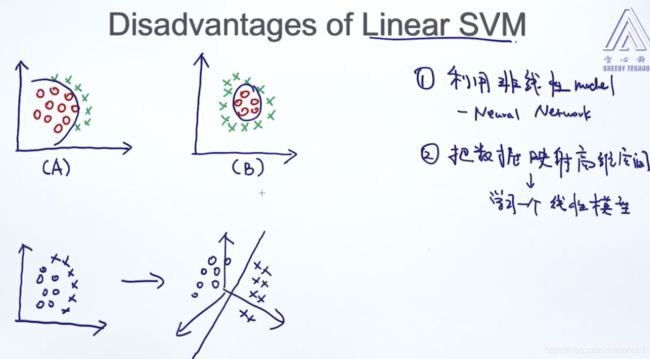
Linear SVM 缺点

  由于线性SVM的决策边界都是线性的，因此下面的截图的非线性SVM的效果不好

解决方案：
1、使用非线性模型，例如：神经网络NN 
2、将数据映射到高维空间，再学习一个线性的模型。