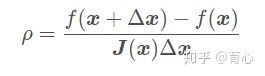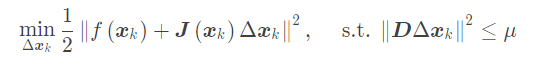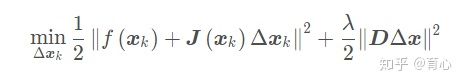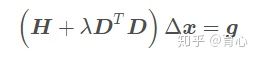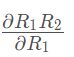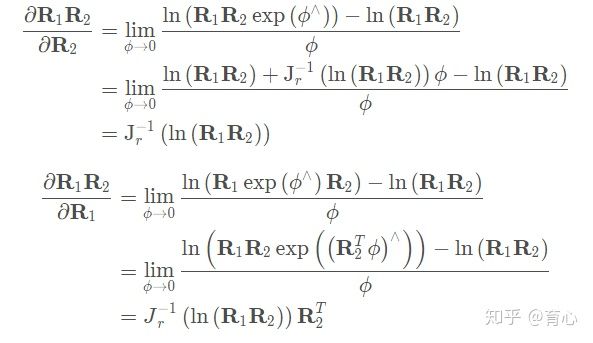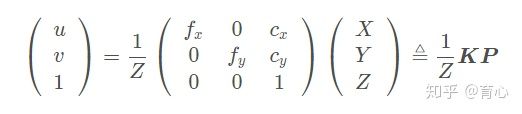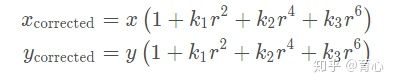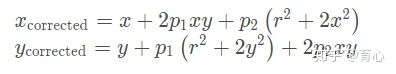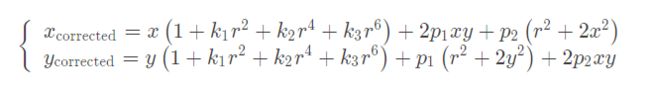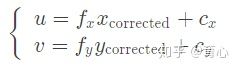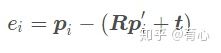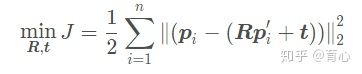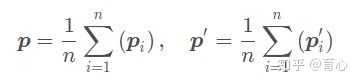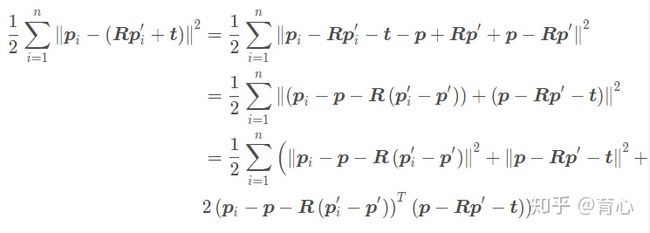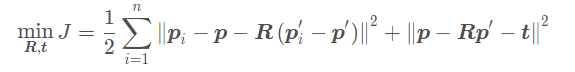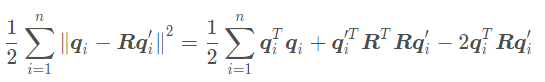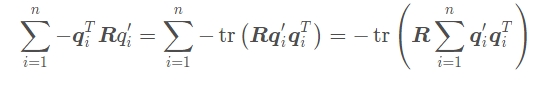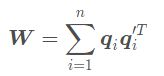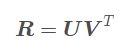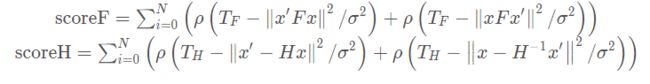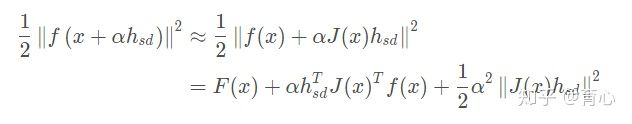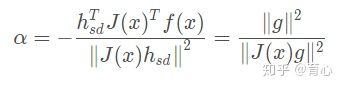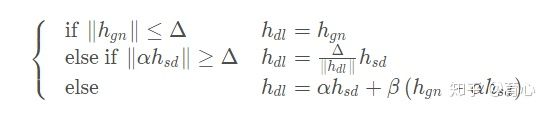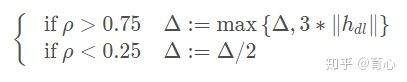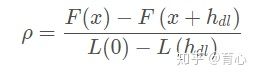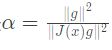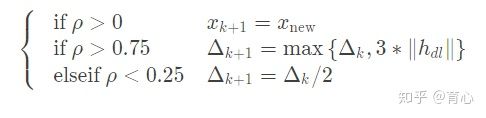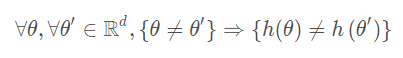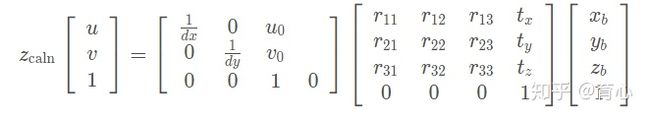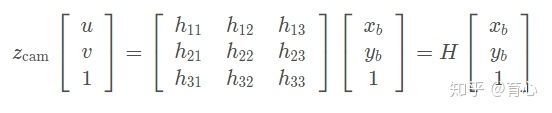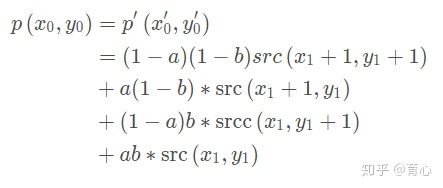slam特征点深度 svd_万字干货！视觉SLAM面试题汇总（19年秋招）——第二部分

上周给大家放松的视觉SLAM面试题汇总（19年秋招）——第一部分，受到了大家的喜爱和众多收藏，原文见育心：视觉SLAM面试题汇总（2019年秋招题库参考）——第一部分

本周福利又双叒叕来了！视觉SLAM面试题汇总（19年秋招）的第二部分为大家倾情放送！点赞关注不迷路！为了保证学习效果，建议大家收藏后细读^-^

以下为本次放送的面试题及解答部分

---

视觉SLAM总结——视觉SLAM面试题汇总（后26个）

26. 除了RANSAC之外，还有什么鲁棒估计的方法？

27. 3D地图点是怎么存储的？表达方式？

28. 给你m相机n个点的bundle adjustment。当我们在仿真的时候，在迭代的时候，相机的位姿会很快的接近真值。而地图点却不能很快的收敛这是为什么呢？

29. LM算法里面那个λ是如何变化的呢？

30. 说一下3D空间的位姿如何去表达?

31. 李群和李代数的关系

32.求导

33. Mat是如何访问元素的？先访问行还是先访问列？

34. 写出单目相机的投影模型，畸变模型。

35. 安装2D lidar的平台匀速旋转的时候，去激光数据畸变，写代码

36. 给两组已经匹配好的3D点，计算相对位姿变换，写代码

37. ORB-SLAM初始化的时候为什么要同时计算H矩阵和F矩阵？

38. 说一下Dog-Leg算法

39. Vins-Mono里面什么是边缘化？First Estimate Jacobian？一致性？可观性？

40. 说一下VINS-Mono的优缺点

41.导一下VINS-Mono里面的预积分公式

42.给定一些有噪声的GPS信号的时候如何去精准的定位？

43.何标定IMU与相机之间的外参数？

44 给你xx误差的GPS，给你xx误差的惯导你怎么得到一个cm级别的地图?

45. 计算H矩阵和F矩阵的时候有什么技巧呢？

46. 给一组点云，从中提取平面。

47. 给一张图片，知道相机与地面之间的相对关系，计算出图的俯视图。

48. 双线性插值如何去做，写公式。

49. RGB-D的SLAM和RGB的SLAM有什么区别？

50.什么是ORB特征? ORB特征的旋转不变性是如何做的? BRIEF算子是怎么提取的?

51.ORB-SLAM中的特征是如何提取的？如何均匀化的？

还是老规矩，先自己想，再看答案哟~^-^

---

26. 除了RANSAC之外，还有什么鲁棒估计的方法？

在《机器人的状态估计》一书中还介绍了M估计（广义的最大似然估计）和协方差估计，所谓M估计指的是加入鲁棒代价函数最大似然估计，而协方差估计指的是同时估计状态和协方差的方法，也称自适应估计。

27. 3D地图点是怎么存储的？表达方式？

以ORB SLAM2为例，3D地图点是以类的形式存储的，在类里面除了存储3D地图点的空间点，同时还存储了3D点的描述子（其实就是BRIFE描述子），用来快速进行与特征点的匹配，同时还用一个map存储了与其有观测关系的关键帧以及其在关键帧中的Index等等。

28. 给你m相机n个点的bundle adjustment。当我们在仿真的时候，在迭代的时候，相机的位姿会很快的接近真值。而地图点却不能很快的收敛这是为什么呢？

约束相机位姿的方程远多于约束地图点的方程

29. LM算法里面那个λ是如何变化的呢？

这里我想从头开始理一遍，参考《视觉SLAM十四讲》首先LM算法优势在哪里，GN法采用雅克比矩阵

的形式来代替难求的海森矩阵，但是

是半正定的，可能出现奇异矩阵或者病态的情况，而且Δx太大的时候也会导致这种二阶泰勒展开的近似不够准确，为解决第二个问题，提出了给Δx添加一个信赖区域方法，也就是LM法，其采用下式判断近似差异的大小进而确定信赖区域范围：

其中分析是实际的代价函数下降值，分母是近似下降值。如果ρ越接近1说明近似越准确，ρ过小说明实际下降较小，需要缩小信赖区域范围，如果ρ过大说明实际下降较大，需要扩大信赖区域范围。其步骤如下：

1.初始化

和优化半径μ；

2.进行迭代求解

这里D为单位阵是信赖区域范围为一个球形

3.计算ρ

4.如果ρ>3/4，则μ=2μ（扩大信赖区域范围）

5.如果ρ=1/4，则μ=0.5μ（缩小信赖区域范围）

6.如果ρ大于某一阈值，则进行更新

这里面需要优化一个带约束的非线性优化函数，采用拉格朗日乘子法就引入了λ，如下

求解后获得

当D=I时有

求解后当λ较小时说明Δx近似于GN方法求解的结果，二阶是较好的近似，而λ较大时说明近似于一阶梯度下降法，二阶近似效果不够好。

30. 说一下3D空间的位姿如何去表达?

李群或者李代数

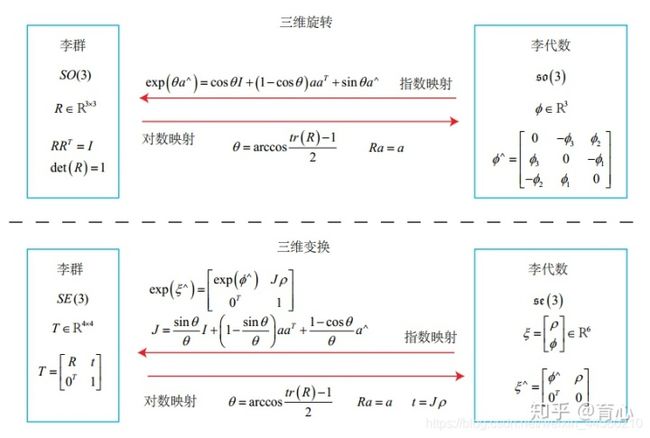
31. 李群和李代数的关系

如上图所示（摘自《视觉SLAM十四讲》），从李群到李代数是对数映射，形式上是先取对数，然后取∨，从李代数到李群是对数映射，形式上先取∧，再取指数，下面具体说：

三维旋转：李群就是三维旋转矩阵，李代数是三维轴角（长度代表旋转大小，方向代表旋转轴方向），从李群到李代数是分别求轴角的角θ(通过矩阵的迹求反余弦)和向量a（旋转矩阵特征值1对应的特征向量），从李代数到李群就是罗德罗杰斯公式。

三维变换：李群是四元变换矩阵，李代数是六维向量，从李群到李代数同样先求角和向量，然后需要求t，从李代数到李群的话通过上面的公式计算。

32. 求导

33. Mat是如何访问元素的？先访问行还是先访问列？

Mat访问像素一共有三种方法：使用at()方法、使用ptr()方法、使用迭代器、使用data指针

（1）使用at()方法：at()方法又是一个模板方法，所以在使用的时候需要传入图像像素的类型，例如：

（2）使用ptr()方法： ptr()方法能够返回指定行的地址（因此正常是先访问行的），然后就可以移动指针访其他的像素。例如

这里需要注意的是，有时候在内存中会为了对齐而对末尾的像素有填充，而有时候没有填充。可以使用isContinue()来访问图像是否有填充，对于没有填充的图像，即连续的图像来说，遍历的时候就可以只要一层循环就可以了，他会自己换行将图像变成一维的来处理。

（3）使用迭代器：对Mat类型来说，他的迭代器类型可以使用MatIterator_或者Mat_::Iterator类型，具体使用如下

用这两个迭代器便可以指定Mat对象的迭代器，注意需要传入模板参数。对迭代器的初始化与C++中的STL一致。

遍历也和前面指针一样，从图像左上角第一个像素开始遍历三个字节，然后第二个字节，依次遍历，到第一行遍历完后，就会到第二行来遍历。

（4）使用data指针：用Mat存储一幅图像时，若图像在内存中是连续存储的（Mat对象的isContinuous == true），则可以将图像的数据看成是一个一维数组，而data（uchar*）成员就是指向图像数据的第一个字节的，因此可以用data指针访问图像的数据，从而加速Mat图像的访问速度。

一般经过裁剪的Mat图像，都不再连续了，如cv::Mat crop_img = src(rect);crop_img 是不连续的Mat图像，如果想转为连续的，最简单的方法，就是将不连续的crop_img 重新clone()一份给新的Mat就是连续的了，例如

34. 写出单目相机的投影模型，畸变模型。

投影模型一般应该都知道写，但是畸变模型就不一定了…参考《视觉SLAM十四讲》

投影模型如下：

注意啊，这里空间点是非齐次坐标，而像素变成了齐次坐标，如果空间点也是齐次坐标的话，需要讲变换矩阵写成3×4

的矩阵，最后一列全为0;。

畸变模型如下：

畸变模型分为径向畸变和切向畸变，径向畸变如下：

切向畸变如下：

组合上面两式，通过五个畸变系数找到空间点在像素平面上的正确位置：

1.将三维空间点P(X,Y,Z)投影到归一化图像平面。设它的归一化坐标为

。

2.对归一化平面上的点进行径向畸变和切向畸变纠正

3.将纠正后的点通过内参数矩阵投影到像素平面，得到该点在图像上的正确位置

值得一提的是，存在两种去畸变处理（Undistort，或称畸变校正）做法。我们可以选择先对整张图像进行去畸变，得到去畸变后的图像，然后讨论此图像上的点的空间位置。或者，我们也可以先考虑图像中的某个点，然后按照去畸变方程，讨论它去畸变后的空间位置。二者都是可行的，不过前者在视觉 SLAM 中似乎更加常见一些。

35. 安装2D lidar的平台匀速旋转的时候，去激光数据畸变，写代码

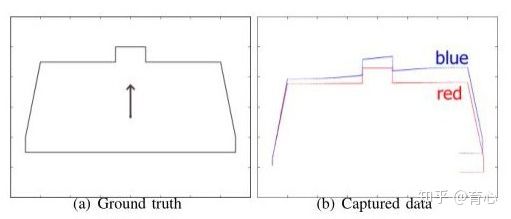
激光雷达里面提到的畸变一般指运动畸变，如果激光数据帧率较同时机器人在运动时就会出现如下图所示情况：

参考激光slam理论与实践（三）：传感器数据处理之激光雷达运动畸变去除

有两种方法：纯估计方法和里程计辅助方法，其中:

纯估计方法：未知对应点的求解方法，采用极大似然估计方法，而已知对应点的话采用ICP，流程如下：

（1）寻找对应点；

（2）根据对应点，计算R与T；

（3）对点云进行转换，计算误差；

（4）不断迭代，直到误差小于某一值。

里程计辅助方法：用CPU读取激光雷达数据，同时单片机上传里程计数据，两者进行时间同步，在CPU上统一进行运动畸变去除，流程如下：

（1）已知当前激光帧的起始时间

，

（2）两个激光束间的时间间隔∗t

（3）里程计数据按照时间顺序存储在一个队列里。

（4）求解当前帧激光数据中的每一个激光点对应的里程计数据（即机器人位姿）

（5）根据求解的位姿把所有的激光点转换到同一坐标系下

（6）重新封装成一帧激光数据发布出去

36. 给两组已经匹配好的3D点，计算相对位姿变换，写代码

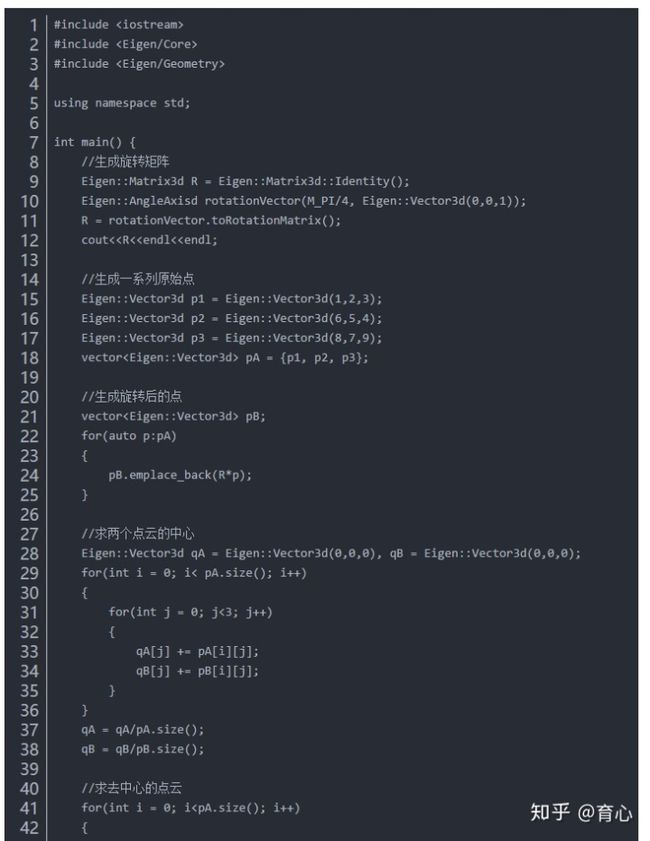
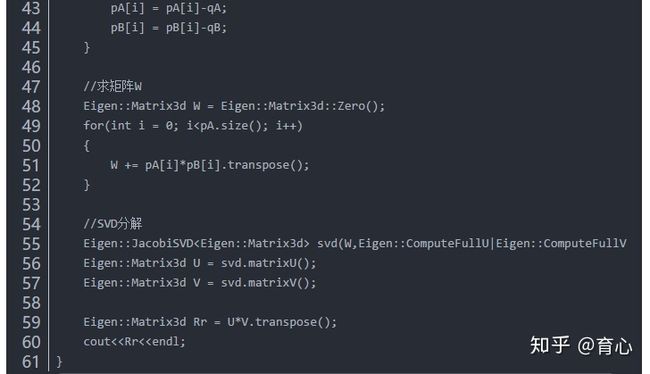
匹配两组已知坐标的3D点当然是采用ICP，参考《视觉SLAM十四讲》，ICP的解法一共有两种：SVD方法和非线性优化方法，下面过一遍SVD方法的推导过程：

构建最小二乘的代价函数，求得使误差平方和达到最小的R,t

定义两组点的质心

对代价函数做如下处理：

上面三项中最后一项求和为零，因此代价函数变为

第一项只和R有关，因此我们可以先求得一个R使得第一项最小然后再求t，我们记去质心的点分别为

和

，我们对第一项展开得：

第一项和第二项都与R无关，因此最后优化目标函数变为：

最后通过SVD方法求得使得上述代价函数最小的R，先定义矩阵：

对其进行SVDF分解

当W满秩时，R为：

解得R后就可以进一步求得t。代码如下：

37. ORB-SLAM初始化的时候为什么要同时计算H矩阵和F矩阵？

简单地说，因为初始化的时候如果出现纯旋转或者所有特征点在同一个平面上的情况，F矩阵会发生自由度退化，而这个时候H矩阵会有较小误差，因此要同时计算H矩阵和F矩阵，那么这里补充两个问题：

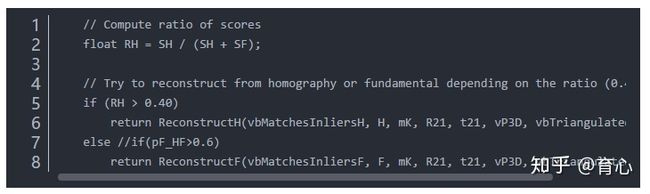
（1）ORB SLAM是怎样选用哪个矩阵去恢复旋转和平移的呢？

这部分代码是这个样子的：

计算SF和SH的公式如下：

其中：

然后SH和SF的比值公式如果结果大于0.4的话就选择H矩阵，如果小于0.4的话就选择F矩阵来进行初始化。

（2）F矩阵退化会发生在哪些情况下？

F矩阵会在两种条件下发生退化，准确地说是三种，第一种是发生在仅旋转的情况下，第二种是发生在所有空间点共面的情况下，第三种是所有空间点和两个摄像机中心在一个二次曲面上，有可能发生退化（第三种情况暂时不予讨论，可参看《多视图几何》一书），下面我们来看下他们为什么会退化：

第一种情况：仅发生旋转，这个比较好理解，基础矩阵满足

在这种情况下，t是零向量，此时求得的基础矩阵是零矩阵，因此无法通过下面的公式求得基础矩阵

第二种情况：所有空间点在一个平面上，这种情况下，匹配点的点集

满足射影棉变换，即

，这时基础矩阵的方程变为

注意这时只要

是一个任意的反对称矩阵都满足这个方程，因此F矩阵可以写成

S为任意的反对称矩阵，因此这种情况下只能求出来的F矩阵是一个三参数簇，而不是一个具体的解。

这里再补充一点，我们还要区分好退化和简化的区别，什么情况下会发生F矩阵的简化呢？

第一种情况：纯平移运动（就是沿着相机坐标系的z轴运动），这种情况下F矩阵简化成了一个反对称矩阵，并且只有两个自由度（反对称矩阵并且尺度不变性），因此两组匹配点就可以求解这种情况，因此这种情况下，上面退化的第二种情况就不会发生了，因为两组匹配点构成的两个空间点肯定都是公面的。

第二种情况：纯平面运动（就是沿着相机坐标系的x轴运动），这种情况下F矩阵的对称部分秩为2（具体为什么可能需要查资料推导了），所以会在原本的F矩阵上再添加一个约束，使得自由度变成六个自由度。

第三种情况：标定之后的情形，其实就是F矩阵在把内参获得之后就变成了E矩阵,自由度变成五个自由度，这个没什么好说的。

38. 说一下Dog-Leg算法

参考非线性最小二乘法之Gauss Newton、L-M、Dog-Leg

Dog-Leg算法是一种高斯牛顿法和最速下降法混合使用的方法，LM法也是这样一种方法，这两者不同的是，LM法采用的是使用一个阻尼项λ来控制下降的速度在一个合理的半径内，如果λ较小的话说明二阶近似较好，方法更加接近于高斯牛顿法，如果λ较大的话说明二阶近似较差，方法更加接近毓最速下降法

Dog-Leg算法是怎么做的呢？在这之前我们要先回顾下最速下降法和高斯牛顿法中：

最速下降法：在《视觉SLAM十四讲》中也提到，最速下降法的增量方向是

，沿着反向梯度方向前进一个补偿λ即可进行梯度下降，那么λ取多少合适呢？十四讲中并没有说，Dog-Leg算法中给出了评判标准：

假设

：

其中

是最速下降法下降方向，使得上式最小，对α 求导得

因此对于最速下降法有

高斯牛顿法：这种方法当中是可以同时求得下降方向和下降大小的

然后接着介绍信赖域，所谓信赖域就是将下降范围控制在这个区域内，在这个范围内二阶泰勒展开能有较好的近似，也即是说不管我们是选择高斯牛顿法还是最速下降法都需要满足

,二阶近似才能较好成立，因此Dog-Leg法给出了如下准则：

其中

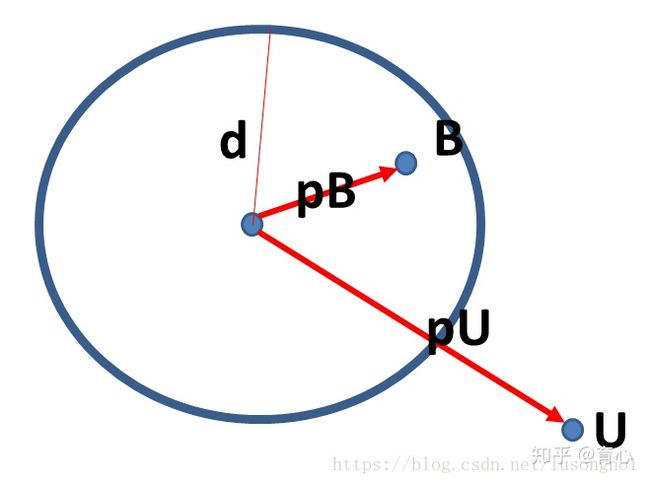
为，上式中第一种情况迭代后下降的点为B点（因为是从另一个博客扒的图，所以里面符号不一样，其中pB指的是高斯牛顿的下降方向，pU指的是最速下降法下降方向）

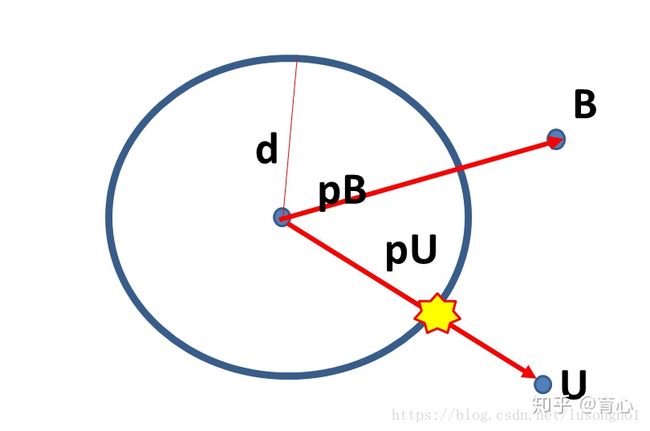
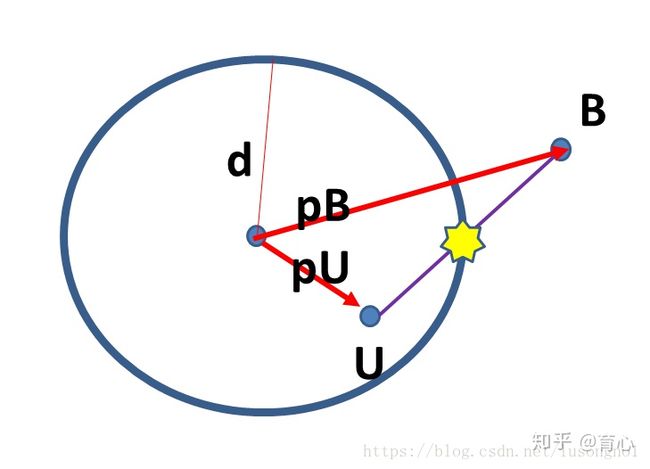
第二种情况为迭代后下降的点为黄色星星点

第二种情况为迭代后下降的点为黄色星星点

由此可见通过上式成功地将下降区域控制在了信赖区域内，那么信赖区域的半径Δ是怎么更新的呢？如下：

其中

综上所述，Dog-Leg的步骤如下：

step1：初始化

step2：求解梯度

，如果

，则退出，否则继续。如果

，则退出，否则继续。

step3：如果半径

，则退出迭代；否则继续；

step4：分别根据GaussNewton法和最快下降法计算

和

，然后计算最快下降法的迭代步长

。

step5：根据

，

和信赖区域半径

，来计算Dog-Leg步进值

。若

，则退出迭代；否则继续。

step6：

，计算增益比

重复step2。

对于ϵ1,ϵ2,ϵ3可以选取任意小的值如

，只是作为迭代的终止条件，其值得选取对最终的收敛结果影响不大。

对比可以进一步发现LM法是通过阻尼器λ控制下降范围的，λ的不同会导致LM法跟接近于高斯牛顿法还是更接近于最速下降法，而Dog-Leg是先计算高斯牛顿法和最速下降法的结果，然后根据两者结果以及信赖区域半径来确定最后迭代采用那个结果。

39. Vins-Mono里面什么是边缘化？First Estimate Jacobian？一致性？可观性？

边缘化其实简单说就是将滑窗中丢弃的图像帧的信息保留下来传递给剩余变量的方式

First Estimate Jacobian是为了解决新测量信息和旧的先验信息构建新的系统时，对某一优化变量求雅克比的线性化点不同导致信息矩阵的零空间发生变化，不可观的变量变成可观变量的问题，做法就是保证变脸的线性化点不变。

一致性应该指的就是线性化点的一致不变，而可观性的定义和现代控制理论中能观性定义是一致的，即通过测量获得状态变量的信息，即该变量是能观的这里给出在深蓝学院的课程中给定一种定义：

对于测量系统 z=h(θ)+ε, 其中

为测量值， θ∈Rd为系统状态量,ε为测量噪声向量。h(·)是个非线性函数，将状态量映射成测量。对于理想数据，如果以下条件成立，则系统状态量θ可观：

40. 说一下VINS-Mono的优缺点

VINS-Mono缺点网上总结得好像不是很多，我根据我的经验总结下面几个缺点：

（1）VINS-Mono的前段是采用的提取关键点然后采用光流法追踪，因此对于弱纹理，关键点少的环境鲁棒性和精度差；

（2）同样还是因为前段的问题，因为没有提取特征描述子，而是使用光流法进行的追踪匹配，一旦画面模糊或者图像丢失，相机就会丢，而且没有重定位模块；

（3）在恒速运动下，会使得IMU有一个自由度不客观，因此会发生漂移。

41. 推导一下VINS-Mono里面的预积分公式

参考博客VINS-Mono关键知识点总结——预积分和后端优化IMU部分

42. 在给定一些有噪声的GPS信号的时候如何去精准的定位？

43. 如何标定IMU与相机之间的外参数？

目前我还没有实际标定过，标定方法可以参考贺博的博客Kalibr 标定双目内外参数以及 IMU 外参数，像Intel出的D435i是已经标定号外参数的，另外在VINS-mono中可以对相机的外参数进行估计。

44. 给你xx误差的GPS，给你xx误差的惯导你怎么得到一个cm级别的地图?

45. 计算H矩阵和F矩阵的时候有什么技巧呢？

其中我能想到的技巧有两点，第一个是RANSAC操作，第二个是归一化操作，RANSAC操作前面已经解释过了，这里主要来分析下归一化操作，在《多视图几何》中提到了一种归一化八点法，方法是先用归一化矩阵对图像坐标进行平移和尺度缩放，然后利用八点法求解单应或者基础矩阵，最后再利用归一化矩阵恢复真实的单应或者基础矩阵，归一化具体操作和优势如下：

具体操作：又称各项同性缩放（非同性缩放有额外开销，但是效果并未提升），步骤如下

（1）对每幅图像中的坐标进行平移（每幅图像的平移不同）使点集的形心移至原点

（2）对坐标系进行缩放使得点x=(x,y,w)中的x,y,w总体上有一样的平均值，注意，对坐标方向，选择的是各向同性，也就是说一个点的x和y坐标等量缩放

（3）选择缩放因子使得点x到原点的平均距离等于

优势：

（1）提高了结果的精度；

（2）归一化步骤通过为测量数据选择有效的标准坐标系，预先消除了坐标变换的影响，使得八点法对于相似变换不变。

46. 给一组点云，从中提取平面。

应该有很多方法的，慢慢补充：

（1）区域生长法：首先依据点的曲率值对点进行排序，之所以排序是因为，区域生长算法是从曲率最小的点开始生长的，这个点就是初始种子点，初始种子点所在的区域即为最平滑的区域，从最平滑的区域开始生长可减少分割片段的总数，提高效率，设置一空的种子点序列和空的聚类区域，选好初始种子后，将其加入到种子点序列中，并搜索邻域点，对每一个邻域点，比较邻域点的法线与当前种子点的法线之间的夹角，小于平滑阀值的将当前点加入到当前区域，然后检测每一个邻域点的曲率值，小于曲率阀值的加入到种子点序列中，删除当前的种子点，循环执行以上步骤，直到种子序列为空

（2）随机抽样一致算法

（3）基于凸包的凹点挖掘算法：

1.提取点云的凸包

2.计算凸包每条边的顶点的点密度（即该点 K 个临近点到该点的距离平均值）

3.如果顶点点密度大于所在边的长度的 X 倍，则删除该边，并从内部点中选择出一个满足夹角最大的点，插入边界边，形成两条新的边界边

4.迭代 2 和 3，一直到全部边界边的 X 倍小于其端点的点密度，算法结束

（4）基于 Delaunay 三角网的轮廓提取算法：

A. 不使用辅助点：

1.首先对点云进行 Delaunay 三角构网

2.同上，判断每条网格边长度的X倍和其端点的点密度之间的大小关系，并删除长的网格边

3.提取只属于一个三角形的边界，作为边界边

4.分类排序，得到有顺序关系的内外轮廓

B. 使用辅助点：

1.手动在点云的边界附近选点

2.Delaunay构网

3.判断每个三角形，如果其中一个点是辅助点，而另外两个点是点云中的点，则连接这两个点做为边界边

4.分类排序，得到有顺序关系的内外轮廓

参考提取平面点云的轮廓

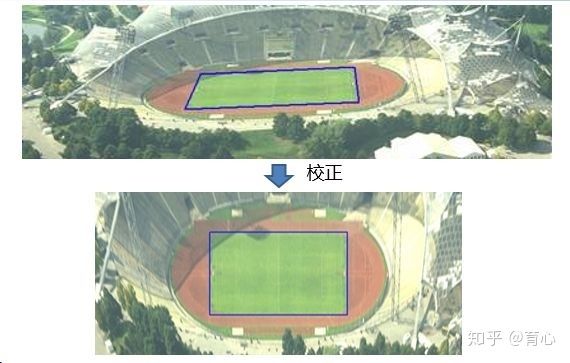
47. 给一张图片，知道相机与地面之间的相对关系，计算出图的俯视图。

参考如何计算一张图片的俯视图？

简单地说利用射影变换，将原本不垂直的线垂直化（用多视图几何上的话说就是消除透视失真），如下图所示

理论推导如下：

从世界坐标系到图像坐标系的变换如下：

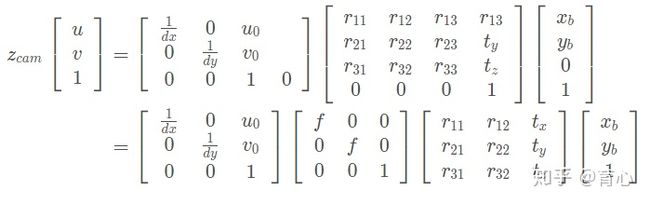
上面的透视变换（射影变换）是将一个平面上的点投影到另外一个平面上去，因此上面的空间点[x0,y0,z0,1] 也在同一平面上，我们不妨设第三维坐标为0，有：

上式可以简化为

这就变化了求解一个单应矩阵，采用四对点就可以进行求解。

因此针对上面那个例子我们的实际操作步骤如下：

（1）灰度化处理

（2）滤波处理

（3）边缘检测

（4）寻找四个点——霍夫变换直线识别

（5）计算 H 矩阵

（6）消除透视失真

48. 双线性插值如何去做，写公式。

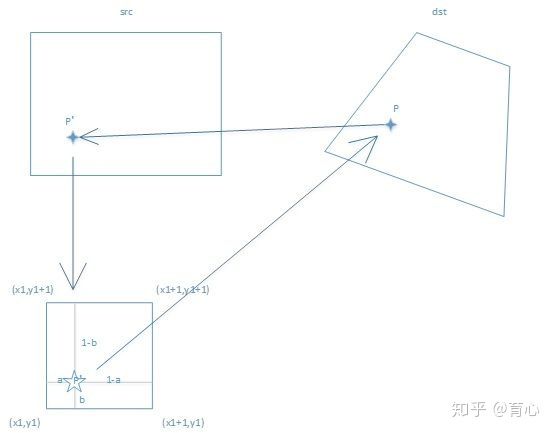
有同学肯定会好奇为嘛会有这个题，这个问题是承接上一个问题来的，在进行透视变换时会遇到的一个实际问题如下图所示

右图（原始图像）中的p点像素(x0,y0)为整数，而到左图中)（变换后的图像）中的p′点像素(x′0,y′0)就不一定是整数，这如何操作呢？一般就是用双线性插值去做。

我们可以发线，p′会落在(x1,y1),(x1+1,y1),(x1+1,y1+1),(x1,y1+1)这四个相邻点的中间，因此我们就要利用(x1,y1),(x1+1,y1),(x1+1,y1+1),(x1,y1+1)，(x1,y1+1),的像素值来计算(x′0,y′0)这点的像素值

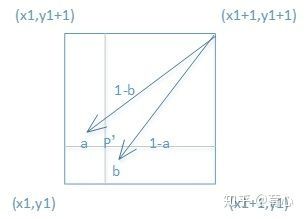
其实很好记忆的，看下面这张图

写公式的话记住(x1+1,y1+1)前面的系数是ab abab

49. RGB-D的SLAM和RGB的SLAM有什么区别？

网上讨论这个的实在太多，我个人觉得单目比较困难点的就是初始化（纯旋转不行，对着平面不行）和尺度问题（需要用Sim解决回环），RGBD-SLAM的话因为有深度因此尺度问题解决了，再环境重建方面会有天然的优势…答得不全，可以再作补充

50. 什么是ORB特征? ORB特征的旋转不变性是如何做的? BRIEF算子是怎么提取的?

ORB特征指的是Oriented FAST and rotated BREIF，包括改进后的FAST角点和BREIF特征子，ORB特征的旋转不变形主要是通过计算半径r范围内像素点的一阶矩，连接质心到特征点的向量作为主方向来对周围像素进行旋转，然后提取BRIEF特征子，BRIEF特征描述子通过计算出来的一个二进制串特征描述符来进行提取的。

51. ORB-SLAM中的特征是如何提取的？如何均匀化的？

ORB描述子的提取流程：

1.输入图像，并对输入图像进行预处理，将其转换成灰度图像；

2.初始化参数，包括特征点数量nfeatures，尺度scaleFactor，金字塔层数nlevel，初始阈值iniThFAST，最小阈值minThFAST等参数；

3.计算金字塔图像，使用8层金字塔，尺度因子为1.2，则通过对原图像进行不同层次的resize，可以获得8层金字塔的图像；

4.计算特征点：

（1）将图像分割成网格，每个网格大小为WW=3030像素；

（2）遍历每个网格；

（3）对每个网格提取FAST关键点，先用初始阈值iniThFAST提取，若提取不到关键点，则改用最小阈值minThFAST提取。（注意，初始阈值一般比最小阈值大）

5.对所有提取到的关键点利用八叉树的形式进行划分：

（1）按照像素宽和像素高的比值作为初始的节点数量，并将关键点坐标落在对应节点内的关键点分配入节点中；

（2）根据每个节点中存在的特征点数量作为判断依据，如果当前节点只有1个关键点，则停止分割。否则继续等分成4份；

（3）按照上述方法不断划分下去，如图所示，可见出现一个八叉树的结构，终止条件是节点的数目Lnode大于等于要求的特征点数量nfeatures；

（4）对满足条件的节点进行遍历，在每个节点中保存响应值最大的关键点，保证特征点的高性能；

6.对上述所保存的所有节点中的特征点计算主方向，利用灰度质心的方法计算主方向，上一讲中我们已经讲解过方法，这讲就不再赘述了；

7.对图像中每个关键点计算其描述子，值得注意的是，为了将主方向融入BRIEF中，在计算描述子时，ORB将pattern进行旋转，使得其具备旋转不变性；参考ORBSLAM2中ORB特征提取的特点

-------------------我是一条可爱的分割线-----------------

（文章转载至深蓝学院学员总结-彭季超）

近期仍然会陆续放送面试题库类文章，点赞加关注，方便及时收取更多干货哟^-^

文章中若有需要讨论的问题，欢迎评论或私信交流！