本系列博客习题来自《算法(第四版)》,算是本人的读书笔记,如果有人在读这本书的,欢迎大家多多交流。为了方便讨论,本人新建了一个微信群(算法交流),想要加入的,请添加我的微信号:zhujinhui207407 谢谢。另外,本人的个人博客 http://www.kyson.cn 也在不停的更新中,欢迎一起讨论
知识点
- java的基本语法:递归调用
- 直方图预习
- 斐波那契数列的递归调用实现以及优化
题目
1.1.15 编写一个静态方法 histogram(),接受一个整型数组 a[] 和一个整数 M 为参数并返回一个大小为 M 的数组,其中第 i 个元素的值为整数 i 在参数数组中出现的次数。如果 a[] 中的值均在 0 到 M-1之间,返回数组中所有元素之和应该和 a.length 相等。
1.1.15 Write a static method histogram() that takes an array a[] of int values and an integer M as arguments and returns an array of length M whose i th entry is the number of times the integer i appeared in the argument array. If the values in a[] are all between 0 and M–1, the sum of the values in the returned array should be equal to a.length.
分析
这道题如果只是看题目的话,绝对会把你绕晕,但如果你看函数的话,一下就豁然开朗了:histogram(直方图),对的,这道题目其实就是让你去实现一个直方图。关于直方图详细,请看这个习题:算法练习(14):直方图(1.1.32)
因此这道题也就有两种解法,一种是按题目上的字面信息解法,另外一种就是我们通过直方图的定义来解答。
答案
解法一:
public static int[] histogram(int[] a,int M)
{
int[] b = new int[M];
int n = 0;
int m = 0;
for(int i = 0; i < M; i++)
{
for(int j = 0; j < a.length ; j++ )
{
if(i == a[j])
{
n++;
}
b[i] = n;
}
n = 0;
}
for(int i = 0 ; i < M ; i++)
{
m = m + b[i];
}
return b;
}
解法二:(感谢读者 蛋黄七分熟 提出)
public static int[] histogram2(int[] a,int M)
{
int[] h = new int[M];
int N = a.length;
for (int i = 0; i < N; i++)
if (a[i] < M)
h[a[i]]++;
return h;
}
测试用例
public static void main(String[] args) {
int a[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 11, 11, 12 };
int M = 13;
int b[] = histogram(a, M);
System.out.println("调用函数后获取的数组:");
for (int i = 0; i < b.length; i++) {
System.out.println(b[i]);
}
}
代码索引
HistogramSample.java
题目
1.1.16 给出 exR1(6) 的返回值:
1.1.16 Give the value of exR1(6):
public static String exR1(int n)
{
if (n <= 0) return "";
return exR1(n-3) + n + exR1(n-2) + n;
}
分析
递归的情况:
f(6)=f(3)+6+f(4)+6
因为f(3)=f(0)+3+f(1)+3 f(0)="" f(1)=f(-2)+1+f(-1)+1=11
所以f(6)=31136+f(4)+6
又因为f(4)=f(1)+4+f(2)+4 f(1)=11 f(2)=f(-1)+2+f(0)+2=22
从而f(6)=311361142246
答案
311361142246
题目
1.1.17 找出以下递归函数的问题:
public static String exR2(int n) {
String s = exR2(n - 3) + n + exR2(n - 2) + n;
if (n <= 0)
return "";
return s;
}
答案
这段代码中的基础情况永远不会被访问。调用 exR2(3) 会产生调用 exR2(0)、exR2(-3) 和exR2(-6),循环往复直到发生 StackOverflowError。
题目
1.1.18 请看以下递归函数:
public static int mystery(int a, int b) {
if (b == 0) return 0;
if (b % 2 == 0) return mystery(a+a, b/2);
return mystery(a+a, b/2) + a;
}
mystery(2, 25) 和 mystery(3, 11) 的返回值是多少?给定正整数 a 和 b,mystery(a,b)计算的结果是什么?将代码中的 + 替换为 * 并将 return 0 改为 return 1,然后回答相同
的问题。
答案
public static int mystery(int a, int b) {
if (b == 0)
return 0;
if (b % 2 == 0)
return mystery(a+a, b/2);
return mystery(a+a, b/2) + a;
}
public static int mystery1(int a, int b) {
if (b == 0)
return 1;
if (b % 2 == 0)
return mystery1(a*a, b/2);
return mystery1(a*a, b/2) * a;
}
public static void main(String args[]) {
System.out.println(mystery(2,25)); // 输出50
System.out.println(mystery(3,11)); //输出33
System.out.println(mystery1(2,25)); // 输出33554432
System.out.println(mystery1(3,11)); //输出177147
}
//这道题目考了一个思想,数据和操作,即第一个参数是数据,第二个参数是操作的。这在实际编程中也是一种解耦的思想
题目
1.1.19 在计算机上运行以下程序:
public class Fibonacci {
public static long F(int N) {
if (N == 0)
return 0;
if (N == 1)
return 1;
return F(N - 1) + F(N - 2);
}
public static void main(String[] args) {
for (int N = 0; N < 100; N++)
StdOut.println(N + " " + F(N));
}
}
计算机用这段程序在一个小时之内能够得到 F(N) 结果的最大 N 值是多少?开发 F(N) 的一个更好的实现,用数组保存已经计算过的值。
答案
public class Fibonacci {
public static long F(int N) {
if (N == 0) return 0;
if (N == 1) return 1;
return F(N-1) + F(N-2);
}
public static void main(String[] args) {
for (int N = 0; N < 100; N++)
StdOut.println(N + " " + F(N));
}
}
//具体能算到多少不知道,部分结果如下:
0 0
1 1
2 1
3 2
4 3
5 5
6 8
7 13
8 21
9 34
10 55
11 89
12 144
13 233
14 377
15 610
16 987
17 1597
18 2584
19 4181
20 6765
21 10946
22 17711
23 28657
24 46368
25 75025
26 121393
27 196418
28 317811
29 514229
30 832040
31 1346269
32 2178309
33 3524578
34 5702887
35 9227465
36 14930352
37 24157817
38 39088169
39 63245986
40 102334155
41 165580141
42 267914296
43 433494437
44 701408733
45 1134903170
46 1836311903
47 2971215073
48 4807526976
49 7778742049
50 12586269025
//这是计算了5分钟左右能计算到第50个,越往后越慢,因为使用了递归的方式,每次的时间都是所有之前的时间的总和
//改良版本:
public class Fibonacci {
public static long F1(int N) {
if (N == 0) return 0;
if (N == 1) return 1;
long f = 0;
long g = 1;
for (int i = 0; i < N ; i++) {
f = f + g;
g = f - g;
}
return f;
}
public static void main(String[] args) {
for (int N = 0; N < 100; N++)
System.out.println(N + " " + F1(N));
}
}
/**需要注意的是,long类型大小限制,后面就会出现负数
81 37889062373143906
82 61305790721611591
83 99194853094755497
84 160500643816367088
85 259695496911122585
86 420196140727489673
87 679891637638612258
88 1100087778366101931
89 1779979416004714189
90 2880067194370816120
91 4660046610375530309
92 7540113804746346429
93 -6246583658587674878
94 1293530146158671551
95 -4953053512429003327
96 -3659523366270331776
97 -8612576878699335103
98 6174643828739884737
99 -2437933049959450366
所以需要替换成其他类型比如BigInteger
*/
1.1.20 编写一个递归的静态方法计算 ln(N!) 的值。
分析
背景知识
- ln是数学中的对数符号。
数学领域自然对数用ln表示,前一个字母是小写的L(l),不是大写的i(I)。
ln 即自然对数 ln=loge a。
以e为底数的对数通常用于ln,而且e还是一个超越数。 - N!是N的阶乘
- 对数的运算法则:两个正数的积的对数,等于同一底数的这两个数的对数的和,即
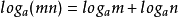
题目中我们使用归纳法来解决问题
令f(N)= ln(N!)
f(1) = ln(1!) = 0
f(2) = ln(2!) = ln(2 * 1) = ln2 + ln1
f(3) = ln(3!) = ln(3 * 2 * 1) = ln3 + ln2 + ln1 = f2 + ln3
f(4) = ln(4!) = ln(4 * 3 * 2 * 1) = ln4 + ln3 + ln2 + ln1 = f(3) + ln4
f(5) = ln(5!) = ln(5 * 4 * 3 * 2 * 1) = ln5 + ln4 + ln3 + ln2 + ln1 = f(4) + ln5
...
f(n) = f(n-1) +lnn
答案
public static double logarithmic(int N) {
if (N == 0)
return 0;
if (N == 1)
return 0;
return (logarithmic(N - 1) + Math.log(N));
}
public static void main(String[] args) {
double result = logarithmic(2);
System.out.println(result);
}
代码索引
Logarithmic.java
题目
1.1.21 编写一段程序,从标准输入按行读取数据,其中每行都包含一个名字和两个整数。然后用printf() 打印一张表格,每行的若干列数据包括名字、两个整数和第一个整数除以第二个整数 的结果,精确到小数点后三位。可以用这种程序将棒球球手的击球命中率或者学生的考试分数 制成表格。
1.1.21 Write a program that reads in lines from standard input with each line containing a name and two integers and then uses printf() to print a table with a column of the names, the integers, and the result of dividing the first by the second, accurate to three decimal places. You could use a program like this to tabulate batting averages for baseball players or grades for students.
分析
关于“标准输入”,本书的库提供了相应的类StdIn来处理,我们来看一下
书中也给出了相应的例子
public class Average
{
public static void main(String[] args)
{ // Average the numbers on StdIn.
double sum = 0.0;
int cnt = 0;
while (!StdIn.isEmpty())
{ // Read a number and cumulate the sum.
sum += StdIn.readDouble();
cnt++;
}
double avg = sum / cnt;
StdOut.printf("Average is %.5f\n", avg);
}
}
答案
public static void main(String[] args) {
int M = 3;
int index = 0;
String[] strs = new String[M];
while (index < M)
strs[index++] = StdIn.readLine();
for (int i = 0; i < strs.length; ++i) {
String[] arr = strs[i].split("\\s+");
double temp = Double.parseDouble(arr[1]) / Double.parseDouble(arr[2]);
StdOut.printf("%-10s %-10s %-10s %-13.3f\n", arr[0], arr[1], arr[2], temp);
}
}
代码索引
Recursion.java
视频讲解
顶级程序员教你学算法(3) :递归(1.1.15-1.1.21)
广告
我的首款个人开发的APP壁纸宝贝上线了,欢迎大家下载。
