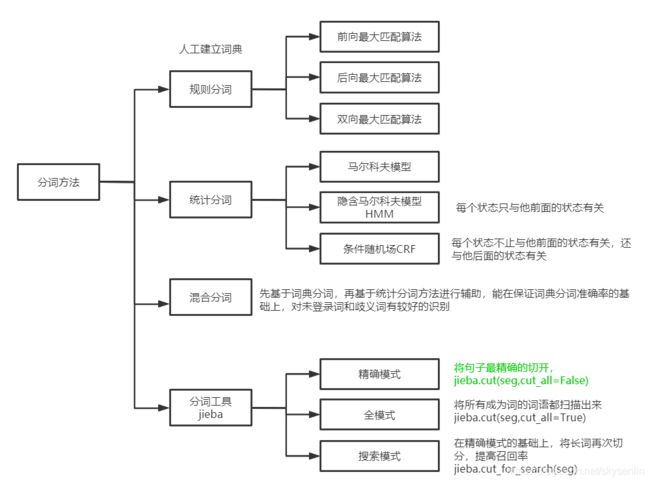
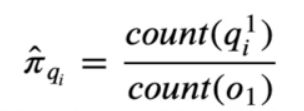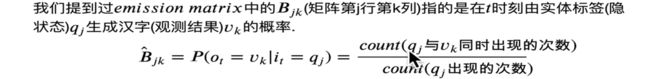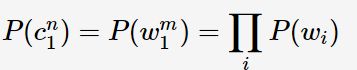自然语言处理训练营NLP--笔记
一、分词
1.1 规则分词
目的:按照最大匹配法(最长字数)分词
参考网址:https://blog.csdn.net/weixin_44735126/article/details/100941826
中文分词时遇到数字、英文、标点等干扰项移除参考地址:https://blog.csdn.net/wiborgite/article/details/79886947?utm_medium=distribute.pc_aggpage_search_result.none-task-blog-2~all~first_rank_v2~rank_v25-2-79886947.nonecase&utm_term=%E4%B8%AD%E6%96%87%E6%96%87%E6%9C%AC%E4%B8%AD%E6%9C%89%E6%95%B0%E5%AD%97%E6%97%A0%E6%B3%95%E5%88%86%E8%AF%8D&spm=1000.2123.3001.4430
分词有3种方法,前向最大匹配算法、后向最大匹配算法、双向最大匹配,他们的共同目的是将一句中文分为若干个词,这些词必须是词典里有的,并且要事先规定一个词包含的最大字数,在此我们规定max_len=5。
1.1.1、前向最大匹配算法
首先我们假设max_len=5,即假设单词最大长度为5;
再假设词典里的单词如下:
[ '岁', '大爷', '玩', '轮滑', '和', '未', '牵绳', '的', '狗', '相撞']
现在我们有一句话:“60岁大爷玩轮滑和未牵绳的狗相撞”
我们移除数字,变成“岁大爷玩轮滑和未牵绳的狗相撞”
分词思想:每次取5个字,去字典查找有没有,没有的话去掉最后一个字继续查,查到后追加到分词结果中:
例:60岁大爷玩轮滑和未牵绳的狗相撞
第一轮:取子串:“岁大爷玩轮”,正向取词,如果匹配失败,每次去除匹配子串最后面一个字
- “岁大爷玩轮”,扫描词典中的5字单词,没有,子串长度减1,子串变为“岁大爷玩”
- “岁大爷玩”,扫描字典中的4字单词,没有,子串长度减1,子串变为“岁大爷”
- “岁大爷”,扫描词典中的3字单词,没有,子串长度减1,子串变为“岁大”
- “岁大”,扫描词典中的2字单词,没有,子串长度减1,子串变为“岁”
- “岁”,扫描词典中的1字单词,匹配成功,输出,输入变成“大爷玩轮滑和未牵绳的狗相撞”
第二轮:子串“大爷玩轮滑”,正向匹配,如果词典中没有,每次减去子串最后面一个字
- “大爷玩轮滑”,扫描词典中5字单词,没有,子串长度减1,子串变为“大爷玩轮”
- “大爷玩轮”,扫描词典中4字单词,没有,子串长度减1,子串变为“大爷玩”
- “大爷玩”,扫描词典中3字单词,没有,子串长度减1,子串变为“大爷”
- “大爷”,扫描词典中2字单词,匹配成功,输出,输入变为“玩轮滑和未牵绳的狗相撞”
以此类推,直到输入的长度为0,停止迭代
最终,前向最大匹配法得到的最终结果为:
[ '岁', '大爷', '玩', '轮滑', '和', '未', '牵绳', '的', '狗', '相撞']
import jieba
import re
import sys
from string import punctuation
if sys.getdefaultencoding() != 'utf-8':
reload(sys) #python在安装时,默认的编码是ascii
sys.setdefaultencoding('utf-8')
# 定义要删除的标点等字符
add_punc=',。、【 】 “”:;()《》‘’{}?!⑦()、%^>℃:.”“^-——=&#@¥'
all_punc=punctuation+add_punc
sentence='60岁ds大爷玩轮滑和?未牵绳的狗相撞.'
sentence_clear=' '.join(jieba.cut(sentence)).split(' ')
sentence_clear_list=[]
#移除数字、标点符号
for i in sentence_clear:
print("i:",i)
#移除英文和数字
i_clear=re.sub(r'[A-Za-z0-9]|/d+','',i)
#移除标点符号
if i_clear in all_punc:
i_clear=''
if len(i_clear)>0:
print("i_clear:",i_clear)
sentence_clear_list.append(i_clear)
print("-"*30)
#清洗后的结果
sentence_clear_result=''.join(sentence_clear_list)
#假设词典
word_dict=['司机', '遇险', '暗', '打手势', '收费员', '秒', '懂', '报警','岁', '大爷', '玩', '轮滑', '和', '未', '牵绳', '的', '狗', '相撞']
#最大单词长度
word_len=5
#句子字数
sentence_len=len(sentence_clear_result)
#从此位置查询5个字
index=0
segmentation=[]
while index
1.1.2、后向最大匹配算法
基本思路和前向分词法一样,只是分词从语句从后向前取词;
我们假设单词最大长度max_len=5;
再假设词典里的单词如下:
['司机', '遇险', '暗', '打手势', '收费员', '秒', '懂', '报警','岁', '大爷', '玩', '轮滑', '和', '未', '牵绳', '的', '狗', '相撞']
现在,我们有一句:“60岁大爷玩轮滑和未牵绳的狗相撞”
分词思想:与前向最大匹配算法类似,只是从后往前匹配词库里的词然后输出。
第一轮:取子串“绳的狗相撞”,后向取词,如果匹配失败,每次去掉匹配子串最前面一个字:
- 子串“绳的狗相撞”,扫描词典中的5字单词,匹配失败,子串长度减1变为“的狗相撞”
- 子串“的狗相撞”,扫描词典中的4字单词,匹配失败,子串长度减1变为“狗相撞”
- 子串“够相撞”,扫描词典中的3字单词,匹配失败,子串长度减1变为“相撞”
- 子串“相撞”,扫描词典中的2字单词,匹配成功,输出,输入变为“岁大爷玩轮滑和未牵绳的狗”
第二轮:取子串“未牵绳的狗”,后向取词
- 子串“未牵绳的狗”,扫描词典中的5字单词,匹配失败,子串长度减1变为“牵绳的狗”
- 子串“牵绳的狗”,扫描词典中的4字单词,匹配失败,子串长度减1变为“绳的狗”
- 子串“绳的狗”,扫描词典中的3字单词,匹配失败,子串长度减1变为“的狗”
- 子串““的狗””,扫描词典中的2字单词,匹配失败,子串长度减1变为“狗”
- 子串“狗”,扫描词典中的1字单词,匹配成功,输出,输入变为“岁大爷玩轮滑和未牵绳的”
以此类推,直到输入长度为0,停止迭代。
最终,后向最大匹配算法的分词结果为:
#清洗后的结果
sentence_clear_result='岁大爷玩轮滑和未牵绳的狗相撞'
#假设词典
word_dict=['司机', '遇险', '暗', '打手势', '收费员', '秒', '懂', '报警','岁', '大爷', '玩', '轮滑', '和', '未', '牵绳', '的', '狗', '相撞']
#最大单词长度
word_len=5
#句子字数
sentence_len=len(sentence_clear_result)
#从此位置查询5个字
index=sentence_len
segmentation=[]
while index>0:
for size in range(index-5,index):
print("size:",size,"index:",index)
piece=sentence_clear_result[size:index]
print(piece)
if piece in word_dict:
print("匹配成功:",piece)
break
print("-"*30)
index=size
segmentation.append(piece)1.1.3、双向最大匹配算法
双向最大匹配算法是对前向最大匹配算法和后向最大匹配算法的结果进行比较,从而给出正确的分词方法。
步骤如下:
1、如果分词结果一样,任取一种结果;
2、分词结果不一样,如果分词数量不一样,取较少词数的分词方法
如果分词数量也一样,取最长单词字数较少的分词方法
如果分词数量一样并且字数也一样,任取一种方法
import jieba
import re
import sys
from string import punctuation
if sys.getdefaultencoding() != 'utf-8':
reload(sys) #python在安装时,默认的编码是ascii
sys.setdefaultencoding('utf-8')
# 定义要删除的标点等字符
add_punc=',。、【 】 “”:;()《》‘’{}?!⑦()、%^>℃:.”“^-——=&#@¥'
all_punc=punctuation+add_punc
def FMM(text,window_size=5):
"""算法:前向最大匹配分词
输入参数:
text:输入文本
window_size:单词最大长度
输出:
分词列表
"""
text_clear=' '.join(jieba.cut(text)).split(' ')
text_clear_list=[]
#移除数字、标点符号
for i in text_clear:
print("i:",i)
#移除英文和数字
i_clear=re.sub(r'[A-Za-z0-9]|/d+','',i)
#移除标点符号
if i_clear in all_punc:
i_clear=''
if len(i_clear)>0:
print("i_clear:",i_clear)
text_clear_list.append(i_clear)
print("-"*30)
#清洗后的结果
text_clear_result=''.join(text_clear_list)
#假设词典
word_dict=['司机', '遇险', '暗', '打手势', '收费员', '秒', '懂', '报警','岁', '大爷', '玩', '轮滑', '和', '未', '牵绳', '的', '狗', '相撞']
#句子字数
text_len=len(text_clear_result)
#从此位置查询5个字
index=0
segmentation=[]
while index0:
print("i_clear:",i_clear)
text_clear_list.append(i_clear)
print("-"*30)
#清洗后的结果
text_clear_result=''.join(text_clear_list)
#假设词典
word_dict=['司机', '遇险', '暗', '打手势', '收费员', '秒', '懂', '报警','岁', '大爷', '玩', '轮滑', '和', '未', '牵绳', '的', '狗', '相撞']
#句子字数
sentence_len=len(text_clear_result)
#从此位置查询5个字
index=sentence_len
segmentation=[]
while index>0:
for size in range(index-5,index):
print("size:",size,"index:",index)
piece=text_clear_result[size:index]
print(piece)
if piece in word_dict:
print("匹配成功:",piece)
break
print("-"*30)
index=size
segmentation.append(piece)
return segmentation
a=FMM('60岁ds大爷玩轮滑和?未牵绳的狗相撞.')
a.sort()
b=BMM('60岁ds大爷玩轮滑和?未牵绳的狗相撞.')
b.sort()
#1、如果前向最大匹配算法分词结果和后向相同,返回任一结果
if a == b:
print(a)
#2.1、如果分词结果不同,取分词次数较少的分词方法
if lena > lenb:
print(b)
if lena < lenb:
print(a)
#2.2、如果前向最大匹配算法分词结果和后向不同,但分词次数相同,返回单词长度较小的分词方法
count1 = 0
count2 = 0
lena = len(a)
lenb = len(b)
if lena == lenb:
for DY1 in a:
if len(DY1) == 5:
count1 = count1 + 1
for DY2 in b:
if len(DY2) == 5:
count2 = count2 + 1
if count1 > count2:
print(b)
else:
print(a)
2、统计分词
相连的字在不同的文本中出现的次数越多,组合频度超过某一个临界值时,此字组可能会构成一个词语,步骤:
1)建立统计语言模型
2)对句子进行单词划分,然后对划分结果进行概率计算,获得概率最大的分词方式
语言模型有以下几种
2.1 语言模型(Language Model LM)
语言模型用来判断:是否一句话从语法上通顺
目标:计算一句话出现的概率
一句话S可以有几种分词方法,为了简单起见,假设有以下三种结果:
![]()
![]()
![]()
最好的分词结果应该保证分完词后这个句子出现的概率最大,其概率满足:
![]()
![]()
为了简化![]() ,我们假设各个分词结果
,我们假设各个分词结果![]() 只与他前k个词相关,即
只与他前k个词相关,即![]()
如果k=1时,各个词是相互独立的,N-gram中的1-gram
![]()
如果k=2时,每个词只与他前面一个词相关,N-gram中的二元语法(bigram,2-gram)
![]()
我们可以在词料库(Corpus)中,数一下![]() 这对词在词料库文本中前后相邻出现多少次(x),以及
这对词在词料库文本中前后相邻出现多少次(x),以及![]() 在同样的词料库文本中出现多少次(y),这这个频数同时除以词料库大小z(可以约去),变得到这个二元组的相对频度:
在同样的词料库文本中出现多少次(y),这这个频数同时除以词料库大小z(可以约去),变得到这个二元组的相对频度:
建立语言模型代码
import jieba
#语料句子
sentence="研究生物很有意思。他大学时代是研究生物的。生物专业是他的首选目标。他是研究生语言模型。"
# dict_ori={}
# ori_list=[]
# sentence_ori_temp=""
#测试句子
sentence_test="他是研究生物的语言模型"
# sentence_test_temp=""
# test_list=[]
# count_list=[]
# p=0
#-------------------------序列标注-----------------------------------------
#训练数据
if sentence.endswith("。"):
sentence=sentence[:-1]
#添加起始符BOS和终止符EOS
sentence_modify_ori1=sentence.replace("。", "EOSBOS")
sentence_modify_ori2="BOS"+sentence_modify_ori1+"EOS"
#测试数据
if sentence_test.endswith("。"):
sentence_test=sentence_test[:-1]
#添加起始符BOS和终止符EOS
sentence_test_modify_test1=sentence_test.replace("。", "EOSBOS")
sentence_test_modify_test2="BOS"+sentence_test_modify_test1+"EOS"
#-------------------------训练数据,目的统计词频-----------------------------------------
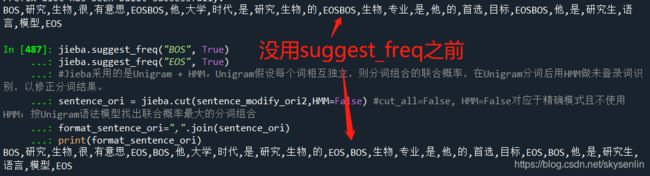
#分词并将结果存入一个list,词频统计结果存入字典,suggest_freq(segment, tune=True)可动态调节单个词语的词频,使其能-参数False(或不能-参数True)分出来。
jieba.suggest_freq("BOS", True)
jieba.suggest_freq("EOS", True)
#Jieba采用的是Unigram + HMM。Unigram假设每个词相互独立,则分词组合的联合概率,在Unigram分词后用HMM做未登录词识别,以修正分词结果。
sentence_ori = jieba.cut(sentence_modify_ori2,HMM=False) #cut_all=False, HMM=False对应于精确模式且不使用HMM;按Unigram语法模型找出联合概率最大的分词组合
format_sentence_ori=",".join(sentence_ori)
print(format_sentence_ori)
#将词按","分割后依次填入数组word_list[]
lists_ori=format_sentence_ori.split(",")
#统计词频,如果词在字典word_dir{}中出现过则+1,未出现则=1
dicts_ori={}
#如果是空字典,为 dict 添加 key-value 对,即统计词出现的频率
if not bool(dicts_ori):
for word in lists_ori:
if word not in dicts_ori:
dicts_ori[word]=1
else:
dicts_ori[word]+=1
#-------------------------测试数据,目的统计词频-----------------------------------------
#分词并将结果存入一个list,词频统计结果存入字典
jieba.suggest_freq("BOS", True)
jieba.suggest_freq("EOS", True)
sentence_test = jieba.cut(sentence_test_modify_test2,HMM=False)
format_sentence_test=",".join(sentence_test)
#将词按","分割后依次填入数组word_list[]
lists_test=format_sentence_test.split(",")
#统计词频,如果词在字典word_dir{}中出现过则+1,未出现则=1
dicts_test={}
#如果是空字典,为 dict 添加 key-value 对,即统计词出现的频率
if not bool(dicts_test):
for word in lists_test:
if word not in dicts_test:
dicts_test[word]=1
else:
dicts_test[word]+=1
#-------------------------#比较两个数列,二元语法-----------------------------------------
#申请空间
count_list=[0]*(len(lists_test))
#遍历测试的字符串
for i in range(0,len(lists_test)-2): ##最后一个词是EOS,倒数第二个词后面没有词结合,没必要统计
#遍历语料字符串,且因为是二元语法,不用比较语料字符串的最后一个字符
for j in range(0,len(lists_ori)-2):#最后两个词是
#如果测试的第一个词和语料的第一个词相等则比较第二个词一个词+EOS,组合没有意义
print("i",i,"j",j,"lists_test[i]",lists_test[i],"lists_ori[j]",lists_ori[j],"lists_test[i+1]",lists_test[i+1],"lists_ori[j+1]",lists_ori[j+1])
if lists_test[i]==lists_ori[j]:
if lists_test[i+1]==lists_ori[j+1]:
print("两重if")
count_list[i]+=1
print("~"*10)
print(count_list)
print("="*30)
lists_ori[len(lists_ori)-2:]
#-------------------------计算一个句子出现的概率-----------------------------------------
flag=0
#概率值为p
p=1
for key in lists_test:
#数据平滑处理:加1法
p*=(float(count_list[flag]+1)/float(dicts_ori[key]+1))
flag+=1 参考网址:语言模型n-gram 视频教学:实现bigram 原始代码:代码
参考网址:python 与自然语言处理之语言模型n-gram
参考网址:语言模型困惑度的两种形式及python实现
语言模型平滑算法:平滑算法
如何让jieba分词不分开某些词(suggest_freq方法的使用):点此链接
瞎聊深度学习——词性标注(jieba词性标注实战:jieba.posseg):点此链接
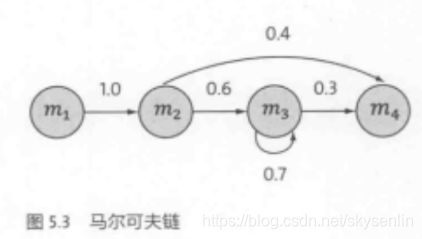
2.2 隐含马尔科夫模型(Hidden Markov Model)
定义:隐马尔可夫模型是关于时序的概率模型。描述由一个隐藏的马尔科夫链随机生成的不可观测的状态随机序列(state sequence),再由各个状态生成一个观测而产生的观测随机序列(observation sequence)的过程,序列的每个位置又可以看作一个时刻。
![]()
![]()
隐含马尔科夫模型是马尔科夫链的一个扩展:任一时刻t的状态![]() 是不可见的。所以观察者没法通过观察到一个状态序列
是不可见的。所以观察者没法通过观察到一个状态序列![]() 来推测转移概率等参数。但是,隐含马尔科夫模型在每个时刻t会输出一个符号
来推测转移概率等参数。但是,隐含马尔科夫模型在每个时刻t会输出一个符号![]() ,而且
,而且![]() 跟
跟![]() 相关且仅跟
相关且仅跟![]() 相关。这个被称为独立输出假设。隐含马尔科夫模型的结构如下:
相关。这个被称为独立输出假设。隐含马尔科夫模型的结构如下:![]() 是一个典型的马尔科夫链。
是一个典型的马尔科夫链。
备注:隐状态![]() 必须是分散的,而观测状态
必须是分散的,而观测状态![]() 可以是连续。
可以是连续。
隐含马尔科夫模型的一个场景是一个人去附近散步、在家打扫、出门游玩是可以观测的,但影响这个人决策的可能是天气原因或节假日因素,是隐含的,我们可以根据观测到序列,推测出隐含的状态有几个,隐含状态之间的转移概率是多少,以及某个隐含状态会发生每种事情的概率是多少。
围绕着隐含马尔科夫模型有3个基本问题:
- 概率计算问题:前向-后向算法----动态规划,给定一个模型λ=(A,B,π)和观测序列O={
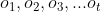 },计算模型λ下观测序列O出现的概率P(O|λ);
},计算模型λ下观测序列O出现的概率P(O|λ); - 学习问题:EM算法,已知O={
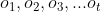 },估计模型λ=(A,B,π)的参数,使得在模型下观测序列P(O|λ)最大;
},估计模型λ=(A,B,π)的参数,使得在模型下观测序列P(O|λ)最大; - 预测问题:Viterbi算法----动态规划,解码问题,已知模型λ=(A,B,π)和观测序列O={
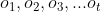 },求给定观测序列条件概率P(S|O,λ)最大的状态序列S。
},求给定观测序列条件概率P(S|O,λ)最大的状态序列S。
HMM的确定
HMM由初始概率分布π、状态转移概率分布A以及观测概率分布B确定。
λ=(A,B,π)![]()
2.2.1 HMM-计算在模型λ下观测序列O出现的概率P(O|λ)-前向算法
实例:假设三个不同的骰子。第一个骰子是我们平常见的骰子(称这个骰子为D6),6个面,第二个骰子是个四面体(称这个骰子为D4),第三个骰子有八个面(称这个骰子为D8),我们用骰子和点数的例子来显示前向概率的计算
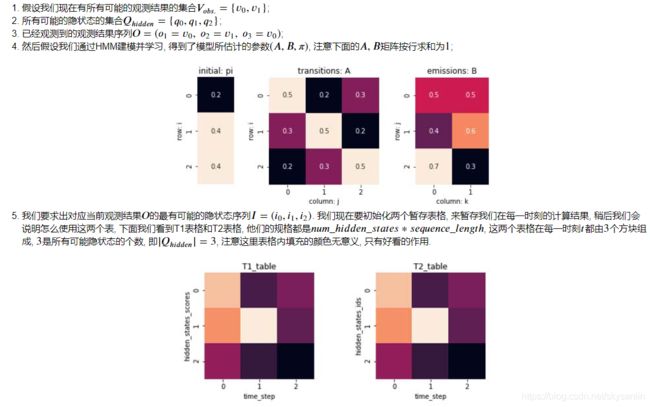
我们的观察集合是:
V={1,2,3,4,5,6,7,8} M=8
我们的状态集合是:
Q={D6,D4,D8} N=3
初始状态分布为
![]()
状态转移概率分布矩阵为
| D6 | D4 | D8 | |
| D6 | 0.5 | 0.2 | 0.3 |
| D4 | 0.3 | 0.5 | 0.2 |
| D8 | 0.2 | 0.3 | 0.5 |
观测状态概率分布矩阵
| O S |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| D6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 0 | 0 |
| D4 | 1/4 | 1/4 | 1/4 | 1/4 | 0 | 0 | 0 | 0 |
| D8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 |
骰子点数观测序列
O={1 6 3}
import numpy as np
states = ('D6', 'D4', 'D8') #状态集合
observations = ('1','2','3','4','5','6','7','8') #观测集合
start_probability = {'D6':1/3, 'D4':1/3, 'D8':1/3}
#转移概率
transition_probability = {
'D6': {'D6':0.5, 'D4':0.2, 'D8':0.3},
'D4': {'D6':0.3, 'D4':0.5, 'D8':0.2},
'D8': {'D6':0.2, 'D4':0.3, 'D8':0.5}
}
#生成概率
emission_probability = {
'D6': {'1': 1/6, '2': 1/6, '3': 1/6, '4': 1/6,'5': 1/6,'6': 1/6,'7': 1/6,'8':1/6},
'D4': {'1': 1/4, '2': 1/4, '3': 1/4, '4': 1/4,'5': 0,'6': 0,'7': 0,'8':0},
'D8': {'1': 1/8, '2': 1/8, '3': 1/8, '4': 1/8,'5': 1/8,'6': 1/8,'7': 1/8,'8':1/8}
}
# 观测序列 O={1 6 3}
obs_seq=('1','6','3')
#矩阵向量化
#转移矩阵
A=np.array([[0.5, 0.2, 0.3],
[0.3, 0.5, 0.2],
[0.2, 0.3, 0.5]])
#生成概率
B=np.array([[0.16666667,0.16666667,0.16666667,0.16666667,0.16666667,0.16666667,0.16666667,0.16666667],
[0.25,0.25,0.25,0.25,0.,0.,0.,0.],
[0.125,0.125,0.125,0.125,0.125,0.125,0.125,0.125]])
#观测集合索引化
observations_index=[0, 1, 2, 3, 4, 5, 6, 7]
#初始概率
pi=np.array([0.33333333, 0.33333333, 0.33333333])
# 观测序列索引化 O={1 6 3}
obs_seq_index=[0,5,2]前向算法计算步骤,首先根据第1次三个状态的前向概率:
第1次是1点,隐藏状态是D6的概率为:
隐藏状态是D4的概率为:
隐藏状态是D8的概率为:
# F对应alpha
N = A.shape[0] #隐藏状态数量
T = len(obs_seq_index) #观测状态数量
F = np.zeros((N,T)) #F最后一列求和代表观察序列产生的概率,行代表某个隐藏状态 列代表第几次或第几个时序 Fij代表第j次i隐藏状态下的产生某个观察的概率
F[:,0] = pi * B[:, obs_seq_index[0]] #第一次观察的发生概率现在我们开始递推了,首先递推第2次三个骰子的前向概率
第2次是6点,
隐藏状态是D6的概率为:
隐藏状态是D4的概率为:
隐藏状态是D8的概率为:
#第2次 6点
#第一次隐藏状态转移到D6 D6索引为0
D6_index=0 #隐藏状态索引位置
obs_index=5 #观察值6点索引 B[D6_index,obs_index]
F[:,1][D6_index]=np.dot(F[:,0],A[:,D6_index])*B[D6_index,obs_index]
#第一次隐藏状态转移到D4
D4_index=1 #隐藏状态索引位置
obs_index=5 #观察值6点索引 B[D4_index,obs_index]
F[:,1][D4_index]=np.dot(F[:,0],A[:,D4_index])*B[D4_index,obs_index]
#第一次隐藏状态转移到D8
D8_index=2 #隐藏状态索引位置
obs_index=5 #观察值6点索引 B[D8_index,obs_index]
F[:,1][D8_index]=np.dot(F[:,0],A[:,D8_index])*B[D8_index,obs_index]继续递推,现在我们第3次是3点三个状态的前向概率:
隐藏状态是D6的概率为:
隐藏状态是D4的概率为:
隐藏状态是D8的概率为:
#第3次 3点
D6_index=0 #隐藏状态索引位置
obs_index=2 #观察值3点索引
F[:,2][D6_index]=np.dot(F[:,1],A[:,D6_index])*B[D6_index,obs_index]
#第一次隐藏状态转移到D4
D4_index=1 #隐藏状态索引位置
obs_index=2 #观察值3点索引
F[:,2][D4_index]=np.dot(F[:,1],A[:,D4_index])*B[D4_index,obs_index]
#第一次隐藏状态转移到D8
D8_index=2 #隐藏状态索引位置
obs_index=2 #观察值3点索引
F[:,2][D8_index]=np.dot(F[:,1],A[:,D8_index])*B[D8_index,obs_index]最终我们求出观测序列:O={1 6 3}的概率为:
F[:,2].sum()前向算法完整代码:
import numpy as np
def generate_index_map(lables):
index_label = {}
label_index = {}
i = 0
for l in lables:
index_label[i] = l
label_index[l] = i
i += 1
return label_index, index_label
def convert_observations_to_index(observations, label_index):
list = []
for o in observations:
list.append(label_index[o])
return list
def convert_map_to_vector(map, label_index):
v = np.empty(len(map), dtype=float)
for e in map:
v[label_index[e]] = map[e]
return v
def convert_map_to_matrix(map, label_index1, label_index2):
m = np.empty((len(label_index1), len(label_index2)), dtype=float)
for line in map:
for col in map[line]:
m[label_index1[line]][label_index2[col]] = map[line][col]
return m
# λ=(A,B,π)
states = ('D6', 'D4', 'D8') #状态集合
observations = ('1','2','3','4','5','6','7','8') #观测结合
start_probability = {'D6':1/3, 'D4':1/3, 'D8':1/3} #初始概率
#转移概率
transition_probability = {
'D6': {'D6':0.5, 'D4':0.2, 'D8':0.3},
'D4': {'D6':0.3, 'D4':0.5, 'D8':0.2},
'D8': {'D6':0.2, 'D4':0.3, 'D8':0.5}
}
#生成概率
emission_probability = {'D6': {'1': 1/6, '2': 1/6, '3': 1/6, '4': 1/6,'5': 1/6,'6': 1/6,'7': 1/6,'8':1/6},
'D4': {'1': 1/4, '2': 1/4, '3': 1/4, '4': 1/4,'5': 0,'6': 0,'7': 0,'8':0},
'D8': {'1': 1/8, '2': 1/8, '3': 1/8, '4': 1/8,'5': 1/8,'6': 1/8,'7': 1/8,'8':1/8}}
states_label_index, states_index_label = generate_index_map(states)
observations_label_index, observations_index_label = generate_index_map(observations)
A = convert_map_to_matrix(transition_probability, states_label_index, states_label_index)
B = convert_map_to_matrix(emission_probability, states_label_index, observations_label_index)
observations_index = convert_observations_to_index(observations, observations_label_index)
pi = convert_map_to_vector(start_probability, states_label_index)
# 观测序列索引化 O={1 6 3}
obs_seq=('1','6','3')
obs_seq_index=[observations_label_index[i] for i in obs_seq]
# F对应alpha
N = A.shape[0] #隐藏状态数量
T = len(obs_seq_index) #观测状态数量
F = np.zeros((N,T)) #列求和代表第几次概率 行代表某个隐藏状态 Fij代表第j次i隐藏状态下的概率
F[:,0] = pi * B[:, obs_seq_index[0]]
for t in range(1, T):
for n in range(N):
print(t,n)
F[n,t] = np.dot(F[:,t-1], (A[:,n])) * B[n, obs_seq_index[t]]
# 观测序列 O={1 6 3} 发生的概率
prob=F[:,T-1].sum()
print(prob)
2.2.2 HMM-计算在模型λ下观测序列O出现的概率P(O|λ)-后向算法
![]()
后向算法计算步骤,首先最后一次三个状态的后向概率初始化:
第3次是3点,隐藏状态是D6的概率为:
![]()
![]()
隐藏状态是D4的概率为:
![]()
隐藏状态是D8的概率为:
![]()
#λ里的参数仍使用前向算法里的参数
# X对应β
N = A.shape[0]
T = len(obs_seq)
X = np.zeros((N,T))
# 初始化时刻T的各个隐藏状态后向概率
X[:,T-1]=1 第2次是6点,
隐藏状态是D6的概率为:
隐藏状态是D4的概率为:
隐藏状态是D8的概率为:
![]()
# 往前递推即第2次,产生6点
# 隐藏状态是D6的概率为:
# 如果第2次是D6,下一个状态的转移概率A[n,:],下一个状态已知概率是X[:,t+1],通过转移概率和已知概率相乘后再相加,相当于把处于i状态分散的概率再集合
t=1
n=0 #D6索引
# 第2次是D6,产生第3次是3点的概率是B[n,obs_seq_index[t+1]]
X[:,t][n]=np.sum(A[n,:]*X[:,t+1]*B[:,obs_seq_index[t+1]])
# 隐藏状态是D4的概率为:
t=1
n=1 #D4索引
# 第2次是D4,产生第3次是3点的概率是B[n,obs_seq_index[t+1]]
X[:,t][n]=np.sum(A[n,:]*X[:,t+1]*B[:,obs_seq_index[t+1]])
# 隐藏状态是D8的概率为:
t=1
n=2 #D8索引
# 第2次是D8,产生第3次是3点的概率是B[n,obs_seq_index[t+1]]
X[:,t][n]=np.sum(A[n,:]*X[:,t+1]*B[:,obs_seq_index[t+1]])继续递推,现在我们第1次是1点三个状态的前向概率:
隐藏状态是D6的概率为:
![]()
![]()
隐藏状态是D4的概率为:
隐藏状态是D8的概率为:
# 往前递推即第1次,第2次产生6点
# 隐藏状态是D6的概率为:
# 如果第2次是D6,下一个状态的转移概率A[n,:],下一个状态已知概率是X[:,t+1],通过转移概率和已知概率相乘后再相加,相当于把处于i状态分散的概率再集合
t=0
n=0 #D6索引
# 第2次是D6,产生第3次是3点的概率是B[n,obs_seq_index[t+1]]
X[:,t][n]=np.sum(A[n,:]*X[:,t+1]*B[:,obs_seq_index[t+1]])
# 隐藏状态是D4的概率为:
t=0
n=1 #D4索引
# 第2次是D4,产生第3次是3点的概率是B[n,obs_seq_index[t+1]]
X[:,t][n]=np.sum(A[n,:]*X[:,t+1]*B[:,obs_seq_index[t+1]])
# 隐藏状态是D8的概率为:
t=0
n=2 #D8索引
# 第2次是D8,产生第3次是3点的概率是B[n,obs_seq_index[t+1]]
X[:,t][n]=np.sum(A[n,:]*X[:,t+1]*B[:,obs_seq_index[t+1]])综合代码如下:
# X对应β
N = A.shape[0]
T = len(obs_seq)
X = np.zeros((N,T))
X[:,-1:] = 1
for t in reversed(range(T-1)):
for n in range(N):
print("t:",t,"n:",n)
print("X[:,t+1]",X[:,t+1],"A[n,:]:",A[n,:],"obs_seq_index[t+1]:",obs_seq_index[t+1],"B[:, obs_seq_index[t+1]]:",B[:, obs_seq_index[t+1]])
X[n,t] = np.sum(X[:,t+1] * A[n,:] * B[:, obs_seq_index[t+1]])
print("="*30)最终我们求出观测序列:O={1 6 3}的概率为:
![]() , 其中
, 其中![]()
O={1 6 3}的概率后向算法为0.04982639,前向算法为0.002896,二者相乘可以解决smoothing算法。
# 后向算法观测序列 O={1 6 3} 发生的概率
prob=X[:,0:1].sum()
print(prob)
HMM前后向算法主要参考:
强烈推荐思想过程和代码实现:http://www.hankcs.com/ml/hidden-markov-model.html
HMM概率问题、学习算法、预测公式大神级细致推导:https://www.bilibili.com/video/BV1MW41167Rf?p=1
通俗易懂:https://www.cnblogs.com/fulcra/p/11065474.html
2.2.2 HMM-学习算法
隐马尔科夫模型的3个基本问题之一:给定足够量的观测数据,如何估计隐含马尔科夫模型的参数,最简单的方式是直接用极大似然估计来估计参数(就是利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值):
1、初始隐状态概率π的参数估计
上式指的是,计算第1时刻,也就是文本中的第一个字,![]() 出现的次数占总第一个字
出现的次数占总第一个字![]() 观测次数(既有多少个句子)的比例。
观测次数(既有多少个句子)的比例。![]() 标1指的是第1时刻,小标i表示第i种隐状态,count是记录次数,具体解释如下图:
标1指的是第1时刻,小标i表示第i种隐状态,count是记录次数,具体解释如下图:
初始隐状态发生的概率为第1刻各个隐状态发生的概率,字位置的4个隐状态B(词首)M(词中) E(词尾)S(单独成词)假设发生了5次即5句话,其中每句话第1个隐状态是B的有3次,是S的有两次,那么
![]()
![]()
![]()
![]()
![]()
['十亿', '中华', '儿女', '踏上', '新', '的', '征', '程', '。']
['B', 'E', 'B', 'E', 'B', 'E', 'B', 'E', 'S', 'S', 'S', 'S', 'S']
==============================
['过去', '的', '一', '年', ',']
['B', 'E', 'S', 'S', 'S', 'S']
==============================
['是', '全国', '各族', '人民', '在', '中国', '共产党', '领导', '下', ',']
['S', 'B', 'E', 'B', 'E', 'B', 'E', 'S', 'B', 'E', 'B', 'M', 'E', 'B', 'E', 'S', 'S']
==============================
['从', '党', '的', '十一届', '三中全会', '实现', '伟大', '历史', '转折', '到', '现在']
['S', 'S', 'S', 'B', 'M', 'E', 'B', 'M', 'M', 'E', 'B', 'E', 'B', 'E', 'B', 'E', 'B', 'E', 'S', 'B', 'E']
==============================
['坚持', '改革', '、', '开放', ',']
['B', 'E', 'B', 'E', 'S', 'B', 'E', 'S']
==============================
['在', '十年动乱', '之后']
['S', 'B', 'M', 'M', 'E', 'B', 'E']
2、转移概率矩阵A的参数估计
我们还利用初始隐状态的数据,统计各个隐状态相邻发生的概率,比如B总共发生23次,其中BB相邻发生0次,BM相邻发生4次,BE相邻发生19次,BS相邻发生0次,那么BB的概率为0/23,BM的概率为4/23,BE的概率为19/23,BS的概率为0/23,依次如下
状态 B M E S
出现次数 23 6 23 20
{'B': {'B': 0/23, 'M': 4/23, 'E': 19/23, 'S': 0/23},
'M': {'B': 0/6, 'M': 2/6, 'E': 4/6, 'S': 0/6},
'E': {'B': 14/23, 'M': 0/23, 'E': 0/23, 'S': 7/23},
'S': {'B': 0.3, 'M': 0.0, 'E': 0.0, 'S': 0.5}}
3、发射概率矩阵B的参数估计
我们还利用初始隐状态的数据,统计各个隐状态生成汉子的数量,比如由B生成的汉字,“中”有2次,“儿”有1次,那么由B生成“中”的概率是(2+1)/23,“儿”的概率是(1+1)/23
各个隐状态生成的汉子数量
{'B': {'中': 2.0, '儿': 1.0, '踏': 1.0, '全': 1.0, '各': 1.0, '人': 1.0, '共': 1.0, '领': 1.0, '十': 2.0, '三': 1.0, '实': 1.0, '伟': 1.0, '历': 1.0, '转': 1.0, '现': 1.0, '改': 1.0, '开': 1.0, '之': 1.0},
'M': {'产': 1.0, '一': 1.0, '中': 1.0, '全': 1.0, '年': 1.0, '动': 1.0},
'E': {'亿': 1.0, '华': 1.0, '女': 1.0, '上': 1.0, '去': 1.0, '国': 2.0, '族': 1.0, '民': 1.0, '党': 1.0, '导': 1.0, '届': 1.0, '会': 1.0, '现': 1.0, '大': 1.0, '史': 1.0, '折': 1.0, '在': 1.0, '持': 1.0, '革': 1.0, '放': 1.0, '乱': 1.0, '后': 1.0},
'S': {'新': 1.0, '的': 3.0, '征': 1.0, '程': 1.0, '。': 1.0, '一': 1.0, '年': 1.0, ',': 3.0, '在': 1.0, '下': 1.0, '党': 1.0, '到': 1.0, '、': 1.0}}
转移概率
{'B': {'中': 3/23, '儿': 2/23, '踏': 0.0869, '全': 0.0869, '各': 0.0869, '人': 0.0869, '共': 0.0869, '领': 0.0869, '十': 0.1304, '三': 0.0869, '实': 0.0869, '伟': 0.0869, '历': 0.0869, '转': 0.0869, '现': 0.0869, '改': 0.0869, '开': 0.0869, '之': 0.0869},
'M': {'产': 0.3333, '一': 0.3333, '中': 0.3333, '全': 0.3333, '年': 0.3333, '动': 0.3333},
'E': {'亿': 0.0869, '华': 0.0869, '女': 0.0869, '上': 0.0869, '去': 0.0869, '国': 0.1304, '族': 0.0869, '民': 0.0869, '党': 0.0869, '导': 0.0869, '届': 0.0869, '会': 0.0869, '现': 0.0869, '大': 0.0869, '史': 0.0869, '折': 0.0869, '在': 0.0869, '持': 0.0869, '革': 0.0869, '放': 0.0869, '乱': 0.0869, '后': 0.08695,
'S': {'新': 0.1, '的': 0.2, '征': 0.1, '程': 0.1, '。': 0.1, '一': 0.1, '年': 0.1, ',': 0.2, '在': 0.1, '下': 0.1, '党': 0.1, '到': 0.1, '、': 0.1}}到此为止,我们就可以遍历所有语料,根据上面的方式得到模型的参数A,B,π的估计,代码如下:
# 状态值集合
state_list = ['B', 'M', 'E', 'S'] #B词首 M词中 E词尾 S单独成词
# 状态转移概率(状态->状态的条件概率)
A_dic = {}
# 发射概率(状态->词语的条件概率)
B_dic = {}
# 状态的初始概率
Pi_dic = {}
#用于统计隐状态出现的数量
Count_dic={}
# 初始化相关参数
for state in state_list:
A_dic[state]={s:0 for s in state_list}
B_dic[state]={}
Pi_dic[state]=0
Count_dic[state]=0
#语料库
sentence_list=['十亿 中华 儿女 踏上 新 的 征 程 。',
'过去 的 一 年 ,',
'是 全国 各族 人民 在 中国 共产党 领导 下 , ',
'从 党 的 十一届 三中全会 实现 伟大 历史 转折 到 现在',
'坚持 改革 、 开放 ,',
'在 十年动乱 之后']
#构词位置标注
def makeLabel(text):
out_text = []
if len(text) == 1:
out_text.append('S')
else:
out_text += ['B'] + ['M'] * (len(text) - 2) + ['E']
return out_text
line_nums=0
words=set()
for line in sentence_list:
line_nums+=1
line=line.strip()
#统计每行中的每个字
word_list=[i for i in line if i !=' ']
words |= set(word_list)
#统计每行每个字的构词位置
line_state=[]
for w in line.split():
line_state.extend(makeLabel(w))
#统计参数
for k,v in enumerate(line_state):
Count_dic[v]+=1
#句子初始状态统计
if k==0:
Pi_dic[v]+=1
else:
A_dic[line_state[k-1]][v]+=1
B_dic[v][word_list[k]]=B_dic[v].get(word_list[k],0)+1
print("="*30)
#初始概率 第1时刻各个隐状态占总记录数比例
Pi_dic={k: v/line_nums for k,v in Pi_dic.items()}
#转移概率
A_dic={k:{k1:v1/Count_dic[k] for k1,v1 in v.items()} for k,v in A_dic.items()}
#发射概率 v1+1是为了解决某些词概率过小,实现平滑
B_dic_1={k:{k1:(v1+1)/Count_dic[k] for k1,v1 in v.items()} for k,v in B_dic.items()}
参考链接:隐马尔可夫模型命名实体识别NER-HMM-从零解读-概率图模型-生成模型
2.2.3 HMM-预测算法--解码--viterbi
![]()
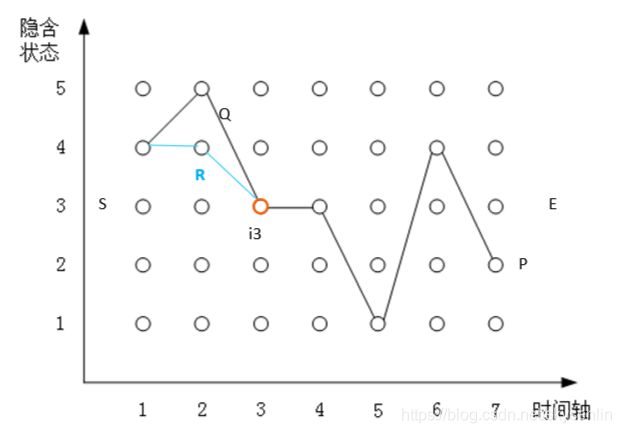
维特比算法的基础:
- 如果最大概率的路径P(或最短路径),经过某个点,比如经过第3时刻的状态
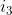 ,那么这条路径上从S到
,那么这条路径上从S到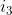 的这一段子路径Q,一定是从S到
的这一段子路径Q,一定是从S到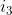 的最短路径,否则,用从S到
的最短路径,否则,用从S到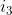 的最短路径R替代Q,构成了一条比P更短的路径,这显然是矛盾的;
的最短路径R替代Q,构成了一条比P更短的路径,这显然是矛盾的;
- 从S到E的路径必定经过第i时刻的某个状态,假定第i时刻有k个状态,那么如果记录了从S到第i时刻(比如第6时刻)所有k个节点的最短路径,最终的最短路径必经过其中的一条。这样,在任何时刻,只要考虑非常有限条候选路径即可。
- 结合上述两点,假定当我们从时刻t进入时刻t+1时,从S到时刻t上各个节点的最大概率(最短)路径已经找到,并且记录到这些节点上,那么在计算从起点S到第t+1时刻的某个状态的最大概率(最短)路径时,只要考虑从S到前一个时刻t所有k个节点的最大概率(最短)路径,以及从这k个节点到t+1时刻的概率即可
我们以实例的方式介绍下维特比算法的计算过程((注意我们在这里下标从0开始算起):),实例如下:
import numpy as np
A = np.array([
[.5, .2, .3],
[.3, .5, .2],
[.2, .3, .5]
])
B = b = np.array([
[.5,.5],
[.4,.6],
[.7,.3]
])
pi = np.array([
[.2],
[.4],
[.4]
])
states = ('q0', 'q1', 'q2') #状态集合
observations= ('v0','v1') #观测集合
obs2idx={'v0':0, 'v1':1} # 观测序列索引化
obs_seq = ('v0','v1','v0')
tag_size=len(states)
seq_len=len(obs_seq)
T1=np.zeros([tag_size,seq_len])
T2=np.zeros([tag_size,seq_len])
HMM的解码就是根据已知的观测序列去预测生成观测序列最大可能概率的状态序列,用的是维特比算法,维特比算法的思想是动态规划,即最终目标可以拆解成4个组成:
- 最终问题和子问题
最终问题如下图所示,生产观测序列(v0,v1,v0,v0,v4,v5,…,v3)最大概率的状态序列如蓝色箭头所示:
子问题:
假设在当前时刻比如第5时刻![]() 最大概率的状态是
最大概率的状态是![]() ,
,![]() 最大概率是从上一状态
最大概率是从上一状态![]() 过来的,依次回溯便组成在第5时刻的最大概率状态序列,那么从第5时刻到最后时刻的路径必然是在这段距离所有路径中最短的路径,否则在第5时刻存在另一个状态
过来的,依次回溯便组成在第5时刻的最大概率状态序列,那么从第5时刻到最后时刻的路径必然是在这段距离所有路径中最短的路径,否则在第5时刻存在另一个状态![]() 到最后时刻的路径最优,那么我们把从第1时刻到最后时刻的路径通过
到最后时刻的路径最优,那么我们把从第1时刻到最后时刻的路径通过![]() 连接起来, 那么就存在两条最优路径从第0时刻到第5时刻,和刚才的假设矛盾。
连接起来, 那么就存在两条最优路径从第0时刻到第5时刻,和刚才的假设矛盾。
最优路径有以下特性: 假设我们有一条最优路径在时刻通过一个隐状态![]() , 那么这一路径从
, 那么这一路径从![]() 到最优路径的终点
到最优路径的终点![]() 相对于在这段距离里所有可能出现的路径里, 也必须是最优的. 否则从
相对于在这段距离里所有可能出现的路径里, 也必须是最优的. 否则从![]() 到
到![]() 就会有更优的一条路径, 如果把他和从
就会有更优的一条路径, 如果把他和从![]() 到
到![]() 的路径(最优路径
的路径(最优路径![]() 之前的部分)连起来, 等于我们又有一条更优路径, 这是矛盾的.
之前的部分)连起来, 等于我们又有一条更优路径, 这是矛盾的.
利用这一特性, 我们只要按上面的步骤计算直到得出最后一步达到的最大概率的隐状态, 再确认最大概率是从前一步哪一个隐状态转移过来的, 然后再回溯直到第一时刻, 就可以找出最优路径了。
- 转移方程
转移方程由两个矩阵组成,T1和T2,T1记录前一状态转移到当前状态的最大概率,T2记录当前最大概率的状态是由前一个状态转移过来的
其行列规格是隐藏状态数量*观察序列长度
- 初始状态和边界
T1的初始状态即第1列,是π(初始状态概率)乘以转移矩阵B得出,T2的初始状态即第1列,其值均是NAN,第一步没有上一状态转移;因为整个维特比算法 是矩阵算法,故没有边界;
T1初始值:
![]()
T2初始值:
![]()
#T1和T2初始化
element=obs_seq[0] #得到第1时刻的观测值
obs_element_token = obs2idx.get(element,0) #得到第1时刻的观测值对应的索引位置
start_Obs_State=B[:,obs_element_token]#得到第1时刻的转移概率
T1[:,0]=pi.flatten()*start_Obs_State
T2[:,0]=np.nan- 计算顺序,
T1和T2均是从前往后计算,T1的每个格子记录从S起始点到当前格子路径的最大概率,T2的每个格子记录着当前格子最大概率是从上一个时刻哪个格子过来的,方便回溯。
#第2时刻i=1-----------------------------------------------------------
#当状态为q0时
i=1 #第i时刻
q=0 #第几个状态
element=obs_seq[i]#观测值
obs_element_token=obs2idx[element] #观测值所在索引
p_obs_state=B[q,obs_element_token] #转移概率
# 上一时刻所有状态概率T1[:,i-1]乘以 由T1时刻各个状态Qj转移到q的转移概率 A[:,q],再乘以转移概率,对比得到最大概率
T1_iq=T1[:,i-1]*A[:,q]*p_obs_state
T1_iq_max=T1_iq.max()
T1[q,i]=T1_iq_max
T2[q,i]=T1_iq.argmax()
q=1 #第几个状态
element=obs_seq[i]#观测值
p_obs_state=B[q,obs_element_token] #转移概率
# 上一时刻所有状态概率T1[:,i-1]乘以 由T1时刻各个状态Qj转移到q的转移概率 A[:,q],再乘以转移概率,对比得到最大概率
T1_iq=T1[:,i-1]*A[:,q]*p_obs_state
T1_iq_max=T1_iq.max()
T1[q,i]=T1_iq_max
T2[q,i]=T1_iq.argmax()
q=2 #第几个状态
element=obs_seq[i]#观测值
p_obs_state=B[q,obs_element_token] #转移概率
# 上一时刻所有状态概率T1[:,i-1]乘以 由T1时刻各个状态Qj转移到q的转移概率 A[:,q],再乘以转移概率,对比得到最大概率
T1_iq=T1[:,i-1]*A[:,q]*p_obs_state
T1_iq_max=T1_iq.max()
T1[q,i]=T1_iq_max
T2[q,i]=T1_iq.argmax()
#第2时刻i=1-----------------------------------------------------------#第3时刻i=2-----------------------------------------------------------
#当状态为q0时
i=2 #第i时刻
q=0 #第几个状态
element=obs_seq[i]#观测值
obs_element_token=obs2idx[element] #观测值所在索引
p_obs_state=B[q,obs_element_token] #转移概率
# 上一时刻所有状态概率T1[:,i-1]乘以 由T1时刻各个状态Qj转移到q的转移概率 A[:,q],再乘以转移概率,对比得到最大概率
T1_iq=T1[:,i-1]*A[:,q]*p_obs_state
T1_iq_max=T1_iq.max()
T1[q,i]=T1_iq_max
T2[q,i]=T1_iq.argmax()
q=1 #第几个状态
element=obs_seq[i]#观测值
p_obs_state=B[q,obs_element_token] #转移概率
# 上一时刻所有状态概率T1[:,i-1]乘以 由T1时刻各个状态Qj转移到q的转移概率 A[:,q],再乘以转移概率,对比得到最大概率
T1_iq=T1[:,i-1]*A[:,q]*p_obs_state
T1_iq_max=T1_iq.max()
T1[q,i]=T1_iq_max
T2[q,i]=T1_iq.argmax()
q=2 #第几个状态
element=obs_seq[i]#观测值
p_obs_state=B[q,obs_element_token] #转移概率
# 上一时刻所有状态概率T1[:,i-1]乘以 由T1时刻各个状态Qj转移到q的转移概率 A[:,q],再乘以转移概率,对比得到最大概率
T1_iq=T1[:,i-1]*A[:,q]*p_obs_state
T1_iq_max=T1_iq.max()
T1[q,i]=T1_iq_max
T2[q,i]=T1_iq.argmax()
#第3时刻i=2-----------------------------------------------------------
# 回溯
#最后一步最大概率的隐状态
best_tag_id = int(np.argmax(T1[:,-1]))
best_tags=[best_tag_id,]
#第2时刻,通过第3时刻追溯第2时刻最大概率状态
i=2 #
best_tag_id=int(T2[best_tag_id,i])
best_tags.append(best_tag_id)
#第1时刻,通过第2时刻追溯第1时刻最大概率状态
i=1
best_tag_id=int(T2[best_tag_id,i])
best_tags.append(best_tag_id)
维特比综合代码:
import numpy as np
def get_p_Obs_State(element,tag_size,obs2idx):
# 计算p( observation | state)
# 如果当前观测值属于未知, 则讲p( observation | state)设为均匀分布
obs_element_token = obs2idx.get(element,-1) #得到第1时刻的观测值对应的索引位置
if obs_element_token == -1:
return np.ones(tag_size)/tag_size
return B[:,obs_element_token]#得到某时刻的转移概率
A = np.array([
[.5, .2, .3],
[.3, .5, .2],
[.2, .3, .5]
])
B = b = np.array([
[.5,.5],
[.4,.6],
[.7,.3]
])
pi = np.array([
[.2],
[.4],
[.4]
])
states = ('q0', 'q1', 'q2') #状态集合
observations= ('v0','v1') #观测集合
obs2idx={'v0':0, 'v1':1} # 观测序列索引化
obs_seq = ('v0','v1','v0')
tag_size=len(states)
seq_len=len(obs_seq)
T1=np.zeros([tag_size,seq_len])
T2=np.zeros([tag_size,seq_len])
#T1和T2初始化
element=obs_seq[0] #得到第1时刻的观测值
obs_element_token = obs2idx.get(element,0) #得到第1时刻的观测值对应的索引位置
start_Obs_State=B[:,obs_element_token]#得到第1时刻的转移概率
T1[:,0]=pi.flatten()*start_Obs_State
T2[:,0]=np.nan
#计算过程
# 第i列某空格计算逻辑 T1[:,i-1]*B*A[:,该空格索引]
for i in range(1,seq_len):
element=obs_seq[i] #得到第1时刻的观测值
p_obs_state=get_p_Obs_State(element,tag_size,obs2idx)#得到第i时刻的转移概率
T1_B_A=T1[:,i-1].reshape(tag_size,-1)*A*p_obs_state #利用了numpy的广播机制,虽然pre_p.shape为(3,),但会随着0轴向下扩展成3行,也可以写成A*np.expand_dims(pre_p, axis=0)
T1[:,i]=np.max(T1_B_A,axis=0)
T2[:,i]=np.argmax(T1_B_A,axis=0)
print(T1,'\n',T2)
# 回溯
best_tag_id = int(np.argmax(T1[:,-1]))
best_tags = [best_tag_id, ]
for i in range(seq_len-1, 0, -1):
best_tag_id = int(T2[best_tag_id,i])
best_tags.append(best_tag_id)
print("最优路径",list(reversed(best_tags))) ![]()
![]()
参考链接:点此链接
参考资料:《数学之美》--吴军
2.2.4 HMM-预测算法--解码--小结
2.3条件随机场CRF
2.4 分词工具
Jieba是由fxsjy大神开源的一款中文分词工具,一款属于工业界的分词工具——模型易用简单、代码清晰可读,推荐有志学习NLP或Python的读一下源码。与采用分词模型Bigram + HMM 的ICTCLAS 相类似,Jieba采用的是Unigram + HMM。Unigram假设每个词相互独立,则分词组合的联合概率:
在Unigram分词后用HMM做未登录词识别,以修正分词结果。
作者:Treant
出处:http://www.cnblogs.com/en-heng/
3、如何衡量分词结果
3.1、分词的一致性
好的方法和坏的方法可以根据分词结果和人工切分的比较来衡量。
3.2、词的颗粒度和层次
分词器同时支持不同层次的词的切分,“清华大学”既可以被看成一个整体,也可以被切分开。
原理和实现:
首先需要一个基本词表和复合词表。基本词表包含像“清华”、“大学”、“贾里尼克”这样无法再分的词。复合词表包含复合词以及它们由哪些基本词构成,比如“清华大学:清华-大学”、“搜索引擎:搜索-引擎”。
接下来需要根据基本词表和复合词表各建立一个语言模型,比如L1和L2。
然后根据基本词表和语言模型L1对句子进行分词,就得到了小颗粒度的分词结果,这里的字串是输入,词串是输出。基本词比较稳定,除了偶尔增加点新词外,不需要额外的研究和工作。
最后,在此基础上,再用复合词表和语言模型L2进行第二次分词,这里输入是基本词串,输出是复合词串。
分词的不一致性可以分为错误和颗粒度不一致性两种。
错误有分成两类,一类是越界性错误,比如把“北京大学生”分成“北京大学-生”。另一类是覆盖性错误,比如把“贾里尼克”分成4个字。这些是明显的错误,是改进分词器时要尽可能要消除的。
颗粒度不一致,人工分词的不一致性大多属于此类,因为不同人的看法左右了对分词器的度量,可以不作为错误,需要做的是尽可能找到各种复合词,完善复合词典。
二、词性标注于命名实体识别
1.1 词性标注对照表--HanLP词性标注集
| 英文 | 中文 | 英文 | 中文 | 英文 | 中文 |
| a | 形容词 | nmc | 化学品名 | udeng | 等 等等 云云 |
| ad | 副形词 | nn | 工作相关名词 | udh | 的话 |
| ag | 形容词性语素 | nnd | 职业 | ug | 过 |
| al | 形容词性惯用语 | nnt | 职务职称 | uguo | 过 |
| an | 名形词 | nr | 人名 | uj | 助词 |
| b | 区别词 | nr1 | 复姓 | ul | 连词 |
| begin | nr2 | 蒙古姓名 | ule | 了 喽 | |
| bg | 区别语素 | nrf | 音译人名 | ulian | 连 (“连小学生都会”) |
| bl | 区别词性惯用语 | nrj | 日语人名 | uls | 来讲 来说 而言 说来 |
| c | 连词 | ns | 地名 | usuo | 所 |
| cc | 并列连词 | nsf | 音译地名 | uv | 连词 |
| d | 副词 | nt | 机构团体名 | uyy | 一样 一般 似的 般 |
| dg | 辄,俱,复之类的副词 | ntc | 公司名 | uz | 着 |
| dl | 连语 | ntcb | 银行 | uzhe | 着 |
| e | 叹词 | ntcf | 工厂 | uzhi | 之 |
| end | 仅用于终##终 | ntch | 酒店宾馆 | v | 动词 |
| f | 方位词 | nth | 医院 | vd | 副动词 |
| g | 学术词汇 | nto | 政府机构 | vf | 趋向动词 |
| gb | 生物相关词汇 | nts | 中小学 | vg | 动词性语素 |
| gbc | 生物类别 | ntu | 大学 | vi | 不及物动词(内动词) |
| gc | 化学相关词汇 | nx | 字母专名 | vl | 动词性惯用语 |
| gg | 地理地质相关词汇 | nz | 其他专名 | vn | 名动词 |
| gi | 计算机相关词汇 | o | 拟声词 | vshi | 动词“是” |
| gm | 数学相关词汇 | p | 介词 | vx | 形式动词 |
| gp | 物理相关词汇 | pba | 介词“把” | vyou | 动词“有” |
| h | 前缀 | pbei | 介词“被” | w | 标点符号 |
| i | 成语 | q | 量词 | wb | 百分号千分号,全角:% ‰ 半角:% |
| j | 简称略语 | qg | 量词语素 | wd | 逗号,全角:, 半角:, |
| k | 后缀 | qt | 时量词 | wf | 分号,全角:; 半角: ; |
| l | 习用语 | qv | 动量词 | wh | 单位符号,全角:¥ $ £ ° ℃ 半角:$ |
| m | 数词 | r | 代词 | wj | 句号,全角:。 |
| mg | 数语素 | rg | 代词性语素 | wky | 右括号,全角:) 〕 ] } 》 】 〗 〉 半角: ) ] { > |
| Mg | 甲乙丙丁之类的数词 | Rg | 古汉语代词性语素 | wkz | 左括号,全角:( 〔 [ { 《 【 〖 〈 半角:( [ { < |
| mq | 数量词 | rr | 人称代词 | wm | 冒号,全角:: 半角: : |
| n | 名词 | ry | 疑问代词 | wn | 顿号,全角:、 |
| nb | 生物名 | rys | 处所疑问代词 | wp | 破折号,全角:—— -- ——- 半角:— —- |
| nba | 动物名 | ryt | 时间疑问代词 | ws | 省略号,全角:…… … |
| nbc | 动物纲目 | ryv | 谓词性疑问代词 | wt | 叹号,全角:! |
| nbp | 植物名 | rz | 指示代词 | ww | 问号,全角:? |
| nf | 食品,比如“薯片” | rzs | 处所指示代词 | wyy | 右引号,全角:” ’ 』 |
| ng | 名词性语素 | rzt | 时间指示代词 | wyz | 左引号,全角:“ ‘ 『 |
| nh | 医药疾病等健康相关名词 | rzv | 谓词性指示代词 | x | 字符串 |
| nhd | 疾病 | s | 处所词 | xu | 网址URL |
| nhm | 药品 | t | 时间词 | xx | 非语素字 |
| ni | 机构相关(不是独立机构名) | tg | 时间词性语素 | y | 语气词(delete yg) |
| nic | 下属机构 | u | 助词 | yg | 语气语素 |
| nis | 机构后缀 | ud | 助词 | z | 状态词 |
| nit | 教育相关机构 | ude1 | 的 底 | zg | 状态词 |
| nl | 名词性惯用语 | ude2 | 地 | ||
| nm | 物品名 | ude3 | 得 |
其他词性标注:点此链接
1.2 命名实体识别
命名实体识别(英语:Named Entity Recognition,简称NER), 是指识别文本中具有特定意义的实体,主要包括人名、地名、机构名、专有名词等等, 并把我们需要识别的词在文本序列中标注出来。
例如有一段文本: 济南市成立自由贸易试验区.
我们要在上面文本中识别一些区域和地点, 那么我们需要识别出来内容有:
济南市(地点), 自由贸易试验区(地点).
在我们今天使用的NER数据集中, 一共有7个标签:
- "B-ORG": 组织或公司(organization)
- "I-ORG": 组织或公司
- "B-PER": 人名(person)
- "I-PER": 人名
- "O": 其他非实体(other)
- "B-LOC": 地名(location)
- "I-LOC": 地名
列出来BIOES分别代表什么意思:
B,即Begin,表示开始
I,即Intermediate,表示中间
E,即End,表示结尾
S,即Single,表示单个字符
O,即Other,表示其他,用于标记无关字符
将“小明在北京大学的燕园看了中国男篮的一场比赛”这句话,进行标注,结果就是:
[B-PER,E-PER,O, B-ORG,I-ORG,I-ORG,E-ORG,O,B-LOC,E-LOC,O,O,B-ORG,I-ORG,I-ORG,E-ORG,O,O,O,O]
那么,换句话说,NER的过程,就是根据输入的句子,预测出其标注序列的过程。
算法:
1)HMM和CRF等机器学习算法
隐马尔科夫的三要素训练代码: (数据源:链接:https://pan.baidu.com/s/1kW1mdLkjHX5vDLzj-VS2hA 提取码:mjb0 )
import numpy as np
from tqdm import tqdm
import os
os.chdir('D:/jupyter/NLP/a_journey_into_math_of_ml-master/05_NER_hidden_markov_model/HMM_model/')
import json
def load_dict(path):
"""
加载字典
:param path:
:return:
"""
with open(path, "r", encoding="utf-8") as f:
return json.load(f)
def load_data(path):
"""
读取txt文件, 加载训练数据
:param path:
:return:
[{'text': ['当', '希', '望', ...],
'label': ... }, {...}, ... ]
"""
with open(path, "r", encoding="utf-8") as f:
return [eval(i) for i in f.readlines()]
char2idx_path="./dicts/char2idx.json"
tag2idx_path="./dicts/tag2idx.json"
# 载入一些字典
# char2idx: 字 转换为 token
char2idx = load_dict(char2idx_path)
# tag2idx: 标签转换为 token
tag2idx = load_dict(tag2idx_path)
# idx2tag: token转换为标签
idx2tag = {v: k for k, v in tag2idx.items()}
# 初始化隐状态数量(实体标签数)和观测数量(字数)
tag_size = len(tag2idx)
vocab_size = max([v for _, v in char2idx.items()]) + 1
# 初始化A, B, pi为全0
transition = np.zeros([tag_size,
tag_size])
emission = np.zeros([tag_size,
vocab_size])
pi = np.zeros(tag_size)
# 偏置, 用来防止log(0)或乘0的情况
epsilon = 1e-8
#/*-----------------------------------------------*/
#/* fit
#/*-----------------------------------------------*/
print("initialize training...")
train_dic_path="./corpus/train_data_1.txt"
train_dic = load_data(train_dic_path)
# 估计转移概率矩阵, 发射概率矩阵和初始概率矩阵的参数
# estimate_transition_and_initial_probs(train_dic)
"""
转移矩阵和初始概率的参数估计, 也就是bigram二元模型
estimate p( Y_t+1 | Y_t )
:param train_dic:
:return:
"""
print("estimating transition and initial probabilities...")
for dic in tqdm(train_dic):
print(dic)
print("="*30)
for i, tag in enumerate(dic["label"][:-1]): #:-1去掉最后一个元素,因为需要解决[i+1]越界
if i == 0:
pi[tag2idx[tag]] += 1
curr_tag = tag2idx[tag]
next_tag = tag2idx[dic["label"][i+1]]
transition[curr_tag, next_tag] += 1
transition[transition == 0] = epsilon
transition /= np.sum(transition, axis=1, keepdims=True) # axis=1 以竖轴为基准 ,同行相加;keepdims主要用于保持矩阵的二维特性
pi[pi == 0] = epsilon
pi /= np.sum(pi)
# estimate_emission_probs(train_dic)
"""
发射矩阵参数的估计
estimate p( Observation | Hidden_state )
:param train_dic:
:return:
"""
print("estimating emission probabilities...")
for dic in tqdm(train_dic):
for char, tag in zip(dic["text"], dic["label"]):
emission[tag2idx[tag],
char2idx[char]] += 1
emission[emission == 0] = epsilon
emission /= np.sum(emission, axis=1, keepdims=True)
# take the logarithm
# 取log防止计算结果下溢
pi = np.log(pi)
transition = np.log(transition)
emission = np.log(emission)
print("DONE!")![]()
参考链接:点此链接
三、关键词提取算法
3.1 TF-IDF
3.2 TEXT-RANK
Text-Rank和PageRank算法相似,都是通过转移矩阵和初始概率的不断迭代得到词(网页)的权重,只是PageRank是无权有向图,Text-Rank是无权无向图,PageRank的转移矩阵通过网页出链数并归一化后求得,而Text-Rank是利用词共现关系得到转移矩阵。
题目描述:
给一段文字,用TEXT-RANK提取其关键词
text='奈飞目前是全世界最大的互联网视频公司,市值超过2000亿美元。奈飞和谷歌旗下的YouTube,两个网站的流量大约占了全球互联网流量的四成。但在20多年前奈飞刚起步的时候,不过是一家租借录像带的小公司。'
过程:
- 1)分句:
我们根据“。.!!??;”等标点符号将文本分成3句:
['奈飞目前是全世界最大的互联网视频公司,市值超过2000亿美元',
'奈飞和谷歌旗下的YouTube,两个网站的流量大约占了全球互联网流量的四成',
'但在20多年前奈飞刚起步的时候,不过是一家租借录像带的小公司']
- 2)分词:
我们根据词性筛选出名词、动词、时间词(an i j l n nr nrfg ns nt nz t v vd vn eng),并去掉停用词,得到分词结果:
[['奈飞', '目前', '全世界', '互联网', '视频', '公司', '市值', '超过'],
['奈飞', '谷歌', '旗下', 'YouTube', '网站', '流量', '占', '全球', '互联网', '流量'],
['奈飞', '租借', '录像带', '小', '公司']]
- 3)构建邻接矩阵:
词与词之间的边,则利用“共现”关系来确定。所谓“共现”,就是共同出现,即在一个给定大小的滑动窗口内的词,认为是共同出现的,而这些单词间也就存在着边,举例:
给定窗口为2,依次滑动:
('奈飞', '目前')
('目前', '全世界')
('全世界', '互联网')
('互联网', '视频')
('视频', '公司')
('公司', '市值')
('市值', '超过')
...
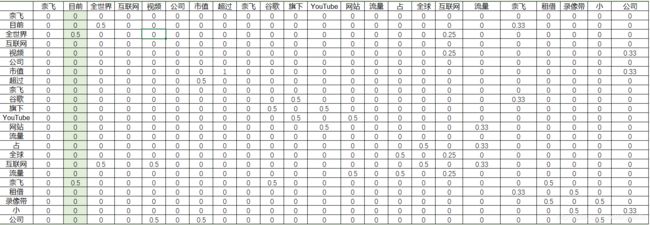
我们需要得到一个邻接矩阵,即一个 n×n 的矩阵,其中 n 表示分词后的单词总数。这个矩阵第 i 行第 j 列的值表示:前一个词是 wi,当前词是 否是wj,是的话是1,1表示无权重,如果是有权重,则这里的1可以替换为相应权重。例如下面这个邻接矩阵:(PS:奈飞在第一行没有数据是因为该词重复,在最下面统计词语共现关系)
可以看到,邻接矩阵是一个对称矩阵,行是奈飞列是目前是共现关系值为1,那么行是目前列是奈飞的值也为1。
有了邻接矩阵,通过标准化,我们可以计算出概率转移矩阵ad_matrix:
- 4)初始概率
#N为单词总数
pr = np.full([N, 1], 1 / N)- 5)加入阻尼因子迭代计算
lpha=0.85
max_iter=100
for _ in range(max_iter):
pr = np.dot(ad_matrix, pr) * alpha + (1 - alpha)
pr = pr / pr.sum() #归一化- 6)对pr排序取前N个关键词
实战
实战代码参照知乎。项目主要结构如下:
-TextRank
--textPro.py : 文本处理,分句分词去停用词,根据词性过滤词。
--textRank.py:实现抽取N个关键词和N个关键句。
--utils.py:共现矩阵的构造,值的计算等。
--const.py:某些常量代码:点此链接
知乎链接:点此链接
上面从原理到实现有了比较初步的了解,下面砍一下jieba的源码,比上面简洁:
基于TextRank算法抽取关键词的主调函数是TextRank.textrank函数,主要是在jieba/analyse/textrank.py中实现。
其中,TextRank是为TextRank算法抽取关键词所定义的类。类在初始化时,默认加载了分词函数和词性标注函数tokenizer = postokenizer = jieba.posseg.dt、停用词表stop_words = self.STOP_WORDS.copy()、词性过滤集合pos_filt = frozenset(('ns', 'n', 'vn', 'v')),窗口span = 5,(("ns", "n", "vn", "v"))表示词性为地名、名词、动名词、动词。
首先定义一个无向有权图,然后对句子进行分词;依次遍历分词结果,如果某个词i满足过滤条件(词性在词性过滤集合中,并且词的长度大于等于2,并且词不是停用词),然后将这个词之后窗口范围内的词j(这些词也需要满足过滤条件),将它们两两(词i和词j)作为key,出现的次数作为value,添加到共现词典中;
然后,依次遍历共现词典,将词典中的每个元素,key = (词i,词j),value = 词i和词j出现的次数,其中词i,词j作为一条边起始点和终止点,共现的次数作为边的权重,添加到之前定义的无向有权图中。
然后对这个无向有权图进行迭代运算textrank算法,最终经过若干次迭代后,算法收敛,每个词都对应一个指标值;
如果设置了权重标志位,则根据指标值值对无向有权图中的词进行降序排序,最后输出topK个词作为关键词;
import jieba
import jieba.posseg
from collections import defaultdict
#定义无向有权图
class UndirectWeightGraph:
d = 0.05
def __init__(self):
self.graph = defaultdict(list)
def addEdge(self, start, end, weight): #添加无向图边
self.graph[start].append((start, end, weight))
self.graph[end].append((end, start, weight))
def rank(self): #根据文本无向图进行单词权重排序,其中包含训练过程
ws = defaultdict(float) #pr值列表
outSum = defaultdict(float) #节点出度列表
ws_init = 1.0/(len(self.graph) or 1.0) #pr初始值
for word, edge_lst in self.graph.items(): #pr, 出度列表初始化
ws[word] = ws_init
outSum[word] = sum(edge[2] for edge in edge_lst)
sorted_keys = sorted(self.graph.keys())
for x in range(10): #多次循环计算达到马尔科夫稳定
for key in sorted_keys:
s = 0
for edge in self.graph[key]:
s += edge[2]/outSum[edge[1]] * ws[edge[1]]
ws[key] = (1 - self.d) + self.d * s
min_rank, max_rank = 100, 0
for w in ws.values(): #归一化权重
if min_rank > w:
min_rank = w
if max_rank < w:
max_rank = w
for key, w in ws.items():
ws[key] = (w - min_rank)*1.0/(max_rank - min_rank)
return ws
import os
class KeywordExtractor(object): #加载停用词表
stop_words = set()
def set_stop_words(self, stop_word_path):
if not os.path.isfile(stop_word_path):
raise Exception("jieba: file does not exit: " + stop_word_path)
f = open(stop_word_path, "r", encoding="utf-8")
for lineno, line in enumerate(f):
self.stop_words.add(line.strip("\n"))
return self.stop_words
class TextRank(KeywordExtractor):
def __init__(self, stop_word_path=None):
self.tokenizer = self.postokenizer = jieba.posseg.dt
if not stop_word_path:
stop_word_path = r"E:\学习相关资料\NLP\停用词表\stopwords-master\百度停用词表.txt"
self.stop_words = KeywordExtractor.set_stop_words(self, stop_word_path=stop_word_path)
self.pos_filter = frozenset(("ns", "n", "vn", "v"))
self.span = 5
def pairfilter(self, wp): # wp 格式为 (flag, word)
state = (wp.flag in self.pos_filter) and (len(wp.word.strip()) >= 2) and (wp.word.lower() not in self.stop_words)
#print("1:", state)
return state
def textrank(self, sentence, topK=20, withWeight=False, allowPOS=("ns", "n", "vn", "v")):
self.pos_filt = frozenset(allowPOS)
g = UndirectWeightGraph()
word2edge = defaultdict(int)
words = tuple(self.tokenizer.cut(sentence))
for i, wp in enumerate(words): #将句子转化为边的形式
#print(wp.flag, wp.word)
if self.pairfilter(wp):
for j in range(i+1, i+self.span):
if j >= len(words):
break
if not self.pairfilter(words[j]):
continue
word2edge[(wp.word, words[j].word)] += 1
for terms, w in word2edge.items():
g.addEdge(terms[0], terms[1], w)
nodes_rank = g.rank()
if withWeight:
tags = sorted(nodes_rank.items(), key=lambda x: x[1], reverse=True)
else:
tags = sorted(nodes_rank)
if topK:
return tags[: topK]
else:
tags
stop_word_path = r"E:\学习相关资料\NLP\停用词表\stopwords-master\百度停用词表.txt"
sentence = r"上海一银行女员工将银行1亿多人民币据为已有,海内外购置10多套房产"
extract_tags = TextRank(stop_word_path=stop_word_path).textrank
print(extract_tags(sentence=sentence, topK=2, withWeight=False))原始链接:点此链接
jieba源码优秀博文:点此链接
3.3 LSI
3.4 LDA
四、句法分析
五、文本向量化
六、情感分析技术
七、NLP中用到的机器学习算法
八、基于深度学习的NLP算法
九、jieba应用
9.1 常用词典
这个网站有很多词典可以下载使用:点此链接
9.2 分词
载入词典
调整词典
9.3 关键词抽取
基于 TF-IDF 算法的关键词抽取
基于 TextRank 算法的关键词抽取
9.4 词性标注







![\alpha_{2}(D6)=[\sum_{j=D6}^{N}\alpha_{1(j)}a_{j-D6}]*B_{D6-O2=6}=[\frac{1}{18}*0.5+\frac{1}{12}*0.3+\frac{1}{24}*0.2]*\frac{1}{6}=0.010185](http://img.e-com-net.com/image/info8/c3170a79f6a94c6eb4dc6a0667c55803.gif)
![\alpha_{2}(D4)=[\sum_{j=D6}^{N}\alpha_{1(j)}a_{j-D4}]*B_{D4-O2=6}=[\frac{1}{18}*0.2+\frac{1}{12}*0.5+\frac{1}{24}*0.3]*0=0](http://img.e-com-net.com/image/info8/5308e98b44974481a918ef22e76ffc5f.gif)
![\alpha_{2}(D8)=[\sum_{j=D6}^{N}\alpha_{1(j)}a_{j-D8}]*B_{D8-O2=6}=[\frac{1}{18}*0.3+\frac{1}{12}*0.2+\frac{1}{24}*0.5]*\frac{1}{8}=0.00677](http://img.e-com-net.com/image/info8/6f0d5b7bff9645b88686afa322bd88e8.gif)
![\alpha_{3}(D6)=[\sum_{j=D6}^{N}\alpha_{2(j)}a_{j-D6}]*B_{D6-O2=3}=[0.010185*0.5+0*0.3+0.00677*0.2]*\frac{1}{6}=0.001074](http://img.e-com-net.com/image/info8/962b72f406ab478480f4a12ab231a75a.gif)
![\alpha_{3}(D4)=[\sum_{j=D4}^{N}\alpha_{2(j)}a_{j-D4}]*B_{D4-O2=3}=[0.010185*0.2+0*0.5+0.00677*0.3]*\frac{1}{4}=0.001017](http://img.e-com-net.com/image/info8/dcbb210510544220a63dbca916484f12.gif)
![\alpha_{3}(D8)=[\sum_{j=D8}^{N}\alpha_{2(j)}a_{j-D8}]*B_{D8-O2=3}=[0.010185*0.3+0*0.2+0.00677*0.5]*\frac{1}{8}=0.000805](http://img.e-com-net.com/image/info8/79261af6e2284cf38b84eb78f596b2ba.gif)
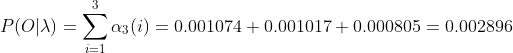


![\beta_{2}(D6)=\sum_{j=D6}^{N}a_{D6-j}*b_{j-2}*\beta_{2+1(j)}=SUM([0.5*\frac{1}{6}*1, 0.2*\frac{1}{4}*1, 0.3*\frac{1}{8}*1])=0.170833](http://img.e-com-net.com/image/info8/1b728143a9d54a11888283586e539fa5.gif)
![\beta_{2}(D4)=\sum_{j=D4}^{N}a_{D4-j}*b_{j-2}*\beta_{2+1(j)}=SUM([0.3*\frac{1}{6}*1, 0.5*\frac{1}{4}*1, 0.2*\frac{1}{8}*1])=0.2](http://img.e-com-net.com/image/info8/e0f9aa4e36af44dd97b30cd1f9487015.gif)
![\beta_{1}(D4)=\sum_{j=D4}^{N}a_{D4-j}*b_{j-5}*\beta_{1+1(j)}=SUM([0.3*\frac{1}{6}*0.17083333, 0.5*0*0.2, 0.2*\frac{1}{8}*0.17083333])=0.0128125](http://img.e-com-net.com/image/info8/1046099c86264904a0368013a77af186.gif)
![\beta_{1}(D8)=\sum_{j=D8}^{N}a_{D8-j}*b_{j-5}*\beta_{1+1(j)}=SUM([0.2*\frac{1}{6}*0.17083333, 0.3*0*0.2, 0.5*\frac{1}{8}*0.17083333])=0.01637153](http://img.e-com-net.com/image/info8/3699c3a2c36a477d950c78d430715169.gif)