一、知识点介绍
1.1 历史模拟法
我们在之前有用到Delta-Normal的GARCH和RiskMetrics方法来计算VaR和ES,假设的是残差满足正态分布,对残差进行二次相关序列的建模并拟合残差,能够得到未来的预测值。而这里说的历史模拟法和蒙特卡罗模拟法跟上面有点不太一样,所基于的前提跟GARCH和RiskMetrics方法认为残差存在着二次自相关不同,本节所涉及到的两种方法也是认为历史可以预测未来(即趋势存在着一定的平稳性),历史模拟法认为历史的分布和未来的分布是一致的,因此历史所计算出来的VaR和ES可以用来代替未来的VaR和ES。有点像电影《土拨鼠之日》不断重复的一天。
1.2 蒙特卡罗模拟法
跟历史模拟法不同,蒙特卡罗模拟法认为的是标准化残差是满足某种分布的(比如说学生t分布),它跟《土拨鼠之日》有些不同,并不是每天的简单重复,有点类似于《楚门的世界》,每天都会有向前一点点的变化,而在这个波动率的变化当中,这里的一点点变化就是标准化残差沿着学生t分布在变动。在这里我有必要解释下标准化残差的概念,其实一开始对这个概念也是糊里糊涂的,但是后来看到代码的实现,其实发现跟标准化正态分布的数据点有点类似。实际上我们在刻画残差的时候,假设说没有其他无关的扰动,数据的数值变动(也就是残差)是完全遵循我们模型算出来的总体标准差sigma的变动的,如果是正态分布,我们应该能看到所有数据点都整整齐齐排在正态分布的曲线上(注意跟数据点出现的顺序无关,并且样本要足够大),但实际上不可能这么理想,本身模拟出来sigma也要变动,并且这个变动(err)我们假设是满足t 学生分布的,那么残差=sigama * err,这里的err是均值为0,标准差为1,自由度为df的标准的t分布,相当于t分布的err其实是一个标准,sigma*err相当于是一个线性的作用(思考利率一定的情况下,本金越多,收益当然越大)。
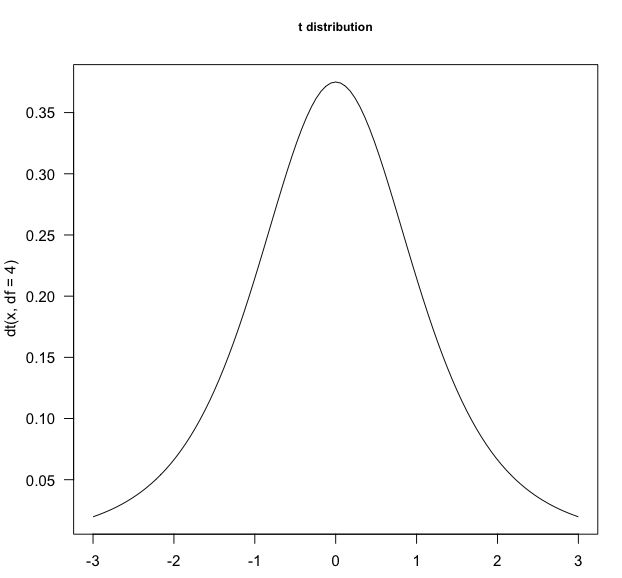
我们绘制一下自由度为4的t分布图。
curve(dt(x,df=4),from=-3, to=3, las='1', main='t distribution', cex.main=0.8)
二、数据处理
2.1 历史模拟法
2.1.1 读取数据
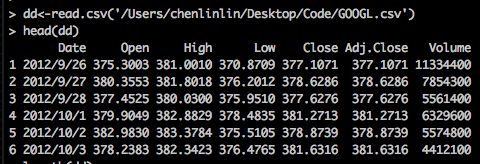
dd<-read.csv('GOOGL.csv')
head(dd)#打印出前几行看一看
dim(dd)#看看data的维度请款
输出结果
从返回的结果来看,数据一共有7列,有1258行。
接下来,我们以收盘价计算出收益率的大小,同样是对数取差。
dd<-diff(log(dd$Adj.Close))
head(dd)#打印出前6行看看结果
2.1.2 计算VaR值
#接下来我重新命名下改为loss,并每个值都转换成百分比的值
loss<- -dd*100
#计算置信水平为95%的分位数
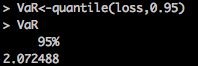
VaR<-quantile(loss,0.95)
接下来我们知道了单日VaR的值是2.072488%,也就是在95%置信水平下的波动率不会超过这个值,这个是单日的,如果是多日的,则要乘以sqrt(T),然后再乘以投资金额就可以了。当然也可以用5天为一个滚动窗口,求平均值以及求这个5天窗口形成的数据的分位数VaR值,这样就不用乘以sqrt(T),但结果应该是有差别的。
2.1.3 计算ES值
ES是指当损失大于VaR以后的损失均值,因此我们通过排序把95%置信区间以后的最大数筛选出来,然后求算术平均就可以了。
sloss<-sort(loss, decreasing=FALSE)#在这里是递增的
ES<-sum(sloss[length(sloss):round(0.95*length(sloss))])/(length(sloss)-round(0.95*length(sloss)))#在这里上面是取前5%的sloss的数进行加和,然后分母是前5%的数据点的个数,整个算数相当于是在求平均值
ES
所计算的单日头寸ES为2.942944%。
2.2 蒙特卡罗模拟法
我们接下来试着用代码来建模预测
步骤如下:
- 建立GARCH模型,预测出均值和方差方程
-
进行蒙特卡罗模拟
其中蒙特卡罗模拟计算VaR和ES的方法思路如下:
最终得到的数据点分布还是按照之前的95%分位点的方法去取得VaR以及计算尾部均值ES。
2.2.1 建立GARCH模型
在这里我们加多一个参数distribution.model='std'表明标准化残差是满足t分布的。
spec3<-ugarchspec(mean.model=list(armaOrder=c(0,0)), variance.model=list(garchOrder=c(1,1)),distribution.model='std')
#拟合模型
fit3<-ugarchfit(data=loss, spec=spec3)
#查看模型的拟合结果
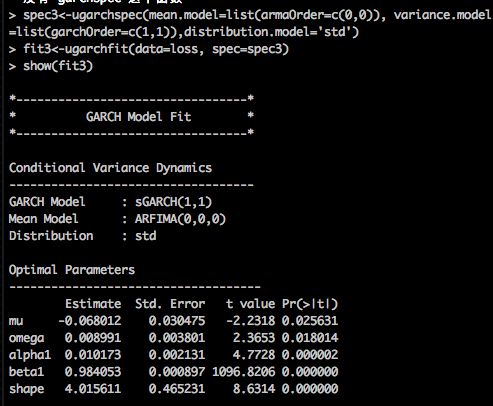
show(fit3)
输出结果
我们之后还要用到这些参数来计算当天的方差->经过标准化t 学生分布转化后的残差->计算出当天的损失率的值->计算出5天损失率的总和
我们先把这些参数都存储起来
mu<-0.068012
alpha<-c(0.008991, 0.010173)
beta<-0.984053
df<-4.015611
#从拟合结果当中提取历史波动率
sig<-sigma(fit3)
2.2.2 进行蒙特卡罗模拟
接下来要初始化一开始的数据值
#设置天数为一周,也就是5天
t<-5
#迭代次数
nround<-3000
#设置随机性,这样你再重新运行代码也是相同的满足随机分布的数字
set.seed(42)
#生成t分布的一个矩阵,行为天数,列为迭代次数
err<-matrix(rstd(t*nround,mean=0,sd=1,nu=df), t, nround)
#设置迭代的起始点,取历史数据的最后一行,包括数据点和标准差
init<-c(loss[1257],sig[1257])
#初始化x_t为空值
xt<-NULL
输出结果
#以init为起点,进行nround轮迭代
for (j in 1:nround){
lt<-NULL#初始化为空值
at<-init[1]-mu#初始化残差
vart<-init[2]^2#初始化方差
for (i in 1:t){
var<-alpha[1]+alpha[2]*at[i]^2+beta*vart[i]#根据GARCH模型拟合出下一期方差
vart<-c(vart,var)#前i期方差
at<-c(at,sqrt(var)*err[i,j])#前i期残差
lt<-c(lt, mu+at[i+1])#前i期的损失变量
}#此循环结束后,得到未来5期的损失变量序列的一次模拟值lt
xt<-c(xt,sum(lt))#未来5期的损失变量的一次总和
}#此循环结束后就得到5期损失变量总和的3000次模拟值
输出结果
#计算VaR值
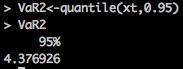
VaR2<-quantile(xt,0.95)
#计算ES
sxt<-sort(xt, decreasing=FALSE)#在这里是递增的
ES2<-sum(sxt[length(sxt):round(0.95*length(sxt))])/(length(sxt)-round(0.95*length(sxt)))
VaR2
ES2
idx<-c(1:nround)[xt>VaR2]#筛选出大于VaR2值的索引
ES3<-mean(xt[idx])#取出大于VaR2值索引对应的值然后求平均
ES3
以另外一种方法打印出ES的均值与排列后的尾部均值是一致的,说明结果比较靠谱。
结果表明,用蒙特卡罗模拟法得到一周的VaR值和尾部均值ES为4.376929%和5.841472%。也就是说在95%的置信水平下,未来一周最大损失率不超过4.376929%,万一发生95%外的损失均值为5.841472%。
三、总结
本文介绍了历史模拟法和蒙特卡罗模拟法计算VaR和ES的实现,历史模拟法比较好理解,但是蒙特卡罗模拟法的流程需要花点心思研究下,并且不同模型的前提是不同的,要关注模型成立的前提条件决定使用什么样的模型。
参考资料
- 实验楼:历史模拟法、蒙特卡罗模拟法计算 VaR 和 ES