Direct3D提高篇:HLSL编程实现PhotoShop滤镜效果 - 锐化模糊

以上两个效果相对比较简单，姑且称之为入门效果， 它并没有用到太多数字图像处理或者信号处理方面的知识。接下来我们要介绍稍微复杂一点的效果，第一个就是图像的模糊和锐化。

图像的模糊又成为图像的平滑(smoothing)，人眼对高频成分是非常敏感的。如果在一个亮度连续变化的图像中，突然出现一个亮点，那么我们很容易察觉出来。类似的，如果图像有个突然的跳跃—明显的边缘，我们也是很容易察觉出来的。这些突然变化的分量就是图像的高频成分。人眼通常是通过低频成分来辨别轮廓，通过高频成分来感知细节的（这也是为什么照片分辨率低的时候，人们只能辨认出照片的大概轮廓，而看不到细节）。但是这些高频成分通常也包含了噪声成分。图像的平滑处理就是滤除图像的高频成分。

那么如何才能滤除图像的高频成分呢？先来介绍一下图像数字滤波器的概念。

简单通俗的来说，图像的数字滤波器其实就是一个n *n的数组（数组中的元素成为滤波器的系数或者滤波器的权重，n称为滤波器的阶）。对图像做滤波的时候，把某个像素为中心的n*n个像素的值和这个滤波器做卷积运算（也就是对应位置上的像素和对应位置上的权重的乘积累加起来），公式如下

 其中x , y 为当前正在处理的像素坐标。

通常情况下，滤波器的阶数为3已经足够了，用于模糊处理的3x3滤波器如下

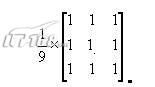
经过这样的滤波器，其实就是等效于把一个像素和周围8个像素一起求平均值，这是非常合理的---等于把一个像素和周围几个像素搅拌在一起—自然就模糊了J

用来对一个图像做滤波处理的函数如下：

剩下的工作就是定义一个用来进行模糊的滤波器模板，并调用dip_filter这个函数就可以了。代码如下：

以上的模糊滤波器称为BOX滤波器，是最简单的滤波器，如果考虑到离开中心像素的距离对滤波器系数的影响，我们通常采用更加合理的滤波器---高斯滤波器—一种通过2维高斯采样得到的滤波器，它的模板如下：

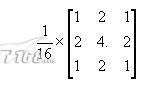
很容易看出来，离开中心越远的像素，权重系数越小。

对于锐化操作，常用的锐化模板是拉普拉斯(Laplacian)模板，这个模板定义如下：

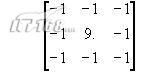
容易看出拉普拉斯模板的作法：先将自身与周围的8个象素相减，表示自身与周围象素的差别；再将这个差别加上自身作为新象素的灰度。如果一片暗区出现了一个亮点，那么锐化处理的结果是这个亮点变得更亮，这就增强了图像的细节。

下面三副图分别表示了经过BOX滤波。高斯滤波和拉普拉斯滤波后的图像

BOX 模糊

高斯模糊

拉普拉斯锐化

高斯模糊和拉普拉斯锐化效果的HLSL和BOX的代码基本一致，就是filter的系数不同，这里不在列出。

通过这个两个效果，我们介绍了图像的滤波操作，这样的操作，也称为模板操作。它实现了一种邻域运算(Neighborhood Operation)，即某个象素点的结果灰度不仅和该象素灰度有关，而且和其邻域点的值有关。模板运算在图像处理中经常要用到，可以看出这是一项非常耗时的运算。有一种优化的方法称为可分离式滤波，就是使用两个pass来进行x/y方向分别滤波，能让运算次数大大减少。而且滤波器阶数越高，优势越明显。

数字图像滤波的时候，同样还需要注意边界像素的问题，不过幸好，HLSL能让边界处理更加的透明和简单。